频数

 

给你 n 个整数 A1,A2,⋯ ,An组成的非降序列。

除此之外，还给你一些由整数 i 和 j（1≤i≤j≤n）组成的查询。对于每个查询，确定在 Ai,⋯ ,Aj中出现次数最多数的频数。

Format
Input
多组数据，读入到0结尾

对于每组数据

第一行包含两个整数 n 和 q。

接下来的一行包含 n 个用空格隔开的整数 A1,⋯ ,An（−100000≤Ai≤100000,i∈{1,2,⋯ ,n}）格隔开。

你可以确定，对于每个 i∈{1,⋯ ,n−1},Ai≤Ai+1

以下 q 行每行一个查询，包含两个整数 i 和 j（1≤i≤j≤n），表明查询的边界。

1≤n,q≤100000间。

Output
对于每个查询，输出一行，一个整数，即在给定范围内出现次数最多数的频数。

Samples
输入数据 1
10 3
-1 -1 1 1 1 1 3 10 10 10
2 3
1 10
5 10
0
输出数据 1
1
4
3

 

 

Sol:

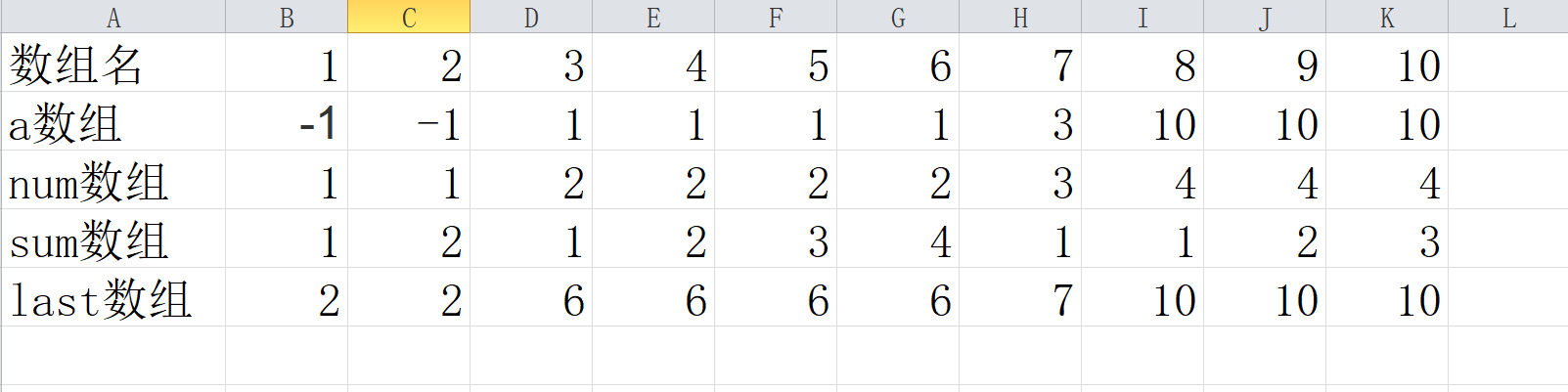
int a[maxn];//读入进来的数字
int sum[maxn];//以第i个位置为止，其代表的数字出现了多少次
int num[maxn];//对读入的数字进行离散化操作，化成1，2，3.....这样的数列
int last[maxn];//last[i]代表第i个位置，它可能向右延伸，记录它最后出现的位置
int f[maxn][22];//针对sum数列建立st表

 

 

 

 

最后，考虑到由于给定的区间，有可能中间某个数字，也就有同一类数字可能有一些在这个区间内，有一些却不在这个区间内。

 

分成下面两种情况

1：给定的区间内只有一种数字

 

2：给定的区间内有多种数字，则挖出第一段的出来。因为它有可能是我们上面所说的“不完整“的。

后面的则rmq算法进行查询。

  

首先用结构体保存元素值X，根据元素值的不同，将同一个值用一个POS下标记录：
-1 -1 1 1 1 1 3 10 10 10 就被记录为 0 0 1 1 1 1 2 3 3 3

然后对元素进行离散化，用一个新的数组R记录每个元素当前出现的次数：
-1 -1 1 1 1 1 3 10 10 10 就被记录为 1 2 1 2 3 4 1 1 2 3

由于给定的区间，有可能中间某个数字，也就有同一类数字可能有一些在这个区间内，有一些却不在这个区间内。

这个其实也是有两种情况

1：前面一段没划在这个区间内，于是其信息不好确定

2：后面一段没划在这个区间内，这个我们在最开始处理时，可以弄出来的。