Kruskal重构树
//https://blog.csdn.net/hwzzyr/article/details/81190442
Kruskal重构树
用于解决图中,有关两点间路径最大值最小化或最小值最大化的问题
如将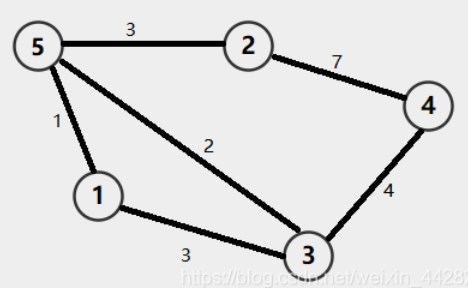
按边权从小到大建立Kruskal重构树,我们就能得到这样的树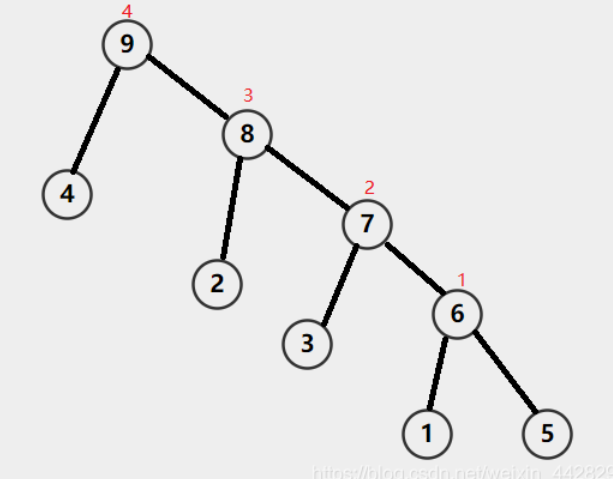
首先Kruskal重构树只有2N-1个节点,只有 N 到 2 N 的点才有权值
而原图中任意两点u,v间路径中最大边权的最小值可以在这颗树中找到,即
val[lca(u,v)]
并且这颗树是一个大根堆,父节点的值大于或等于子节点的值
同理,如果我们按边权从大到小建立Kruskal重构树,我们就能得到这样的树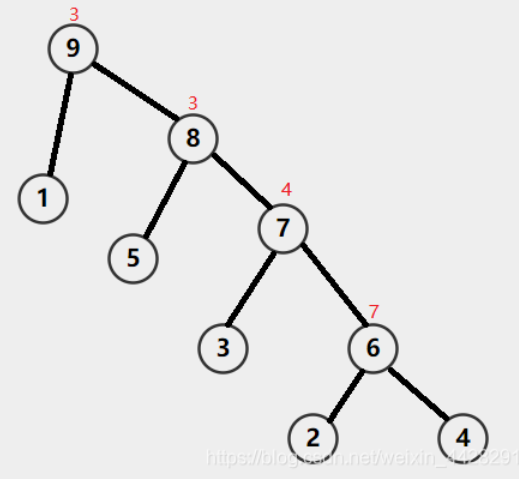
原图中任意两点u,v间路径中最小边权的最大值可以在这颗树中找到,即val[lca(u, v)]
并且这颗树是一个小根堆,父节点的值小于或等于子节点的值
https://blog.csdn.net/weixin_44282912/article/details/105821573

# include <iostream>
# include <stdio.h>
# include <stdlib.h>
# include <algorithm>
# include <string.h>
# define IL inline
# define ll long long
# define Fill(a, b) memset(a, b, sizeof(a));
using namespace std;
IL ll Read(){
char c = '%'; ll x = 0, z = 1;
for(; c < '0' || c > '9'; c = getchar()) z = c == '-' ? -1 : 1;
for(; c >= '0' && c <= '9'; c = getchar()) x = x * 10 + c - '0';
return x * z;
}
const int MAXN = 20001, MAXM = 200001;
int ft[MAXN], n, m, cnt, fa[MAXN][20], w[MAXN], deep[MAXN], Fa[MAXN], num;
struct Edge{
int to, nt;
} edge[MAXM];
struct Kruskal{
int u, v, f;
IL bool operator <(Kruskal b) const{
return f > b.f;
}
} road[MAXM];
IL int Find(int x){
return Fa[x] == x ? x : Fa[x] = Find(Fa[x]);
}
IL void Add(int u, int v){
edge[cnt] = (Edge){v, ft[u]}; ft[u] = cnt++;
edge[cnt] = (Edge){u, ft[v]}; ft[v] = cnt++;
}
IL void Dfs(int u){
for(int e = ft[u]; e != -1; e = edge[e].nt){
int v = edge[e].to;
if(!deep[v]){
deep[v] = deep[u] + 1;
fa[v][0] = u;
Dfs(v);
}
}
}
IL int LCA(int u, int v){
if(Find(u) != Find(v)) return -1;
if(deep[u] < deep[v]) swap(u, v);
for(int i = 18; i >= 0; i--)
if(deep[fa[u][i]] >= deep[v]) u = fa[u][i];
if(u == v) return w[u];
for(int i = 18; i >= 0; i--)
if(fa[u][i] != fa[v][i]) u = fa[u][i], v = fa[v][i];
return w[fa[u][0]];
}
int main(){
Fill(ft, -1);
num = n = Read(); m = Read();
for(int i = 1; i <= 2 * n; i++)
Fa[i] = i;
for(int i = 1; i <= m; i++)
road[i] = (Kruskal){Read(), Read(), Read()};
sort(road + 1, road + m + 1);
for(int i = 1, tot = 0; i <= m && tot < n; i++){
int u = Find(road[i].u), v = Find(road[i].v);
if(u != v){
tot++;
w[++num] = road[i].f;
Fa[u] = Fa[v] = num;
Add(u, num); Add(v, num);
}
}
for(int i = num; i; i--)
if(!deep[i]) deep[i] = 1, Dfs(i);
for(int i = 1; i <= 18; i++)
for(int j = 1; j <= num; j++)
fa[j][i] = fa[fa[j][i - 1]][i - 1];
int Q = Read();
while(Q--){
int u = Read(), v = Read();
printf("%d\n", LCA(u, v));
}
return 0;
}
Description
给你N个点的无向图 (1 <= N <= 15,000),记为:1…N。
图中有M条边 (1 <= M <= 30,000) ,第j条边的长度为:
d_j ( 1 < = d_j < = 1,000,000,000).
现在有 K个询问 (1 < = K < = 15,000)。
每个询问的格式是:A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?
Input
第一行: N, M, K。
第2..M+1行: 三个正整数:X, Y, and D (1 <= X <=N; 1 <= Y <= N). 表示X与Y之间有一条长度为D的边。
第M+2..M+K+1行: 每行两个整数A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?
Output
对每个询问,输出最长的边最小值是多少。
Sample Input
6 6 8
1 2 5
2 3 4
3 4 3
1 4 8
2 5 7
4 6 2
1 2
1 3
1 4
2 3
2 4
5 1
6 2
6 1
Sample Output
5
5
5
4
4
7
4
5
HINT
1 <= N <= 15,000
1 <= M <= 30,000
1 <= d_j <= 1,000,000,000
1 <= K <= 15,000
正解:最小生成树+倍增lca
解题报告:
大概题意是给定一个无向图,然后求两点之间的路径中权值最大的边的最小值
望着这道题10分钟之后感觉做不到一眼秒题,老老实实画图,结果发现我真是太弱了,居然没有发现满足题意的条件竟然是最小生成树的性质。。。
显然先构出最小生成树,其他的边是没有用的,可以删掉。
构出最小生成树之后,就考虑两点间的路径上的最大值。
可以在求lca的时候顺便维护一下就可以了。
我开始打了一个树链剖分+线段树,然而上午脑袋不是很清白,而且鬼畜的BZOJ,居然迷之RE了两次。
好吧,被迫改用倍增,然后就过了,并不知道为什么树链剖分哪里打萎了。
(这道题其实就是NOIP2013的原题货车运输的改版的好吗,几乎一模一样)
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<vector>
#include<queue>
#include<string>
#ifdef WIN32
#define OT "%I64d"
#else
#define OT "%lld"
#endif
using namespace std;
typedef long long LL;
int n,m;
int u[200011],to[200011],w[200011];
int first[200011],next[200011],u1[200011],to1[200011],ww[200011];
int father[200011],height[200011];
int f[100011][16],quan[100011][16];
inline int getint(){
int q=0,w=0;
char c=getchar();
while(c!='-' && ( c<'0' || c>'9' ) ) c=getchar();
if(c=='-') q=1,c=getchar();
while(c>='0' && c<='9') w=w*10+c-'0',c=getchar();
return q?-w:w;
}
inline void qsort(int l,int r)
{
int i=l,j=r;
int mid=w[(i+j)/2],p;
do
{
while(w[i]<mid)i++;
while(w[j]>mid)j--;
if(i<=j)
{
p=w[i];w[i]=w[j];w[j]=p;
p=u[i];u[i]=u[j];u[j]=p;
p=to[i];to[i]=to[j];to[j]=p;
i++;
j--;
}
}while(i<=j);
if(i<r)qsort(i,r);
if(l<j)qsort(l,j);
}
inline int find(int x){
if(father[x]!=x) father[x]=find(father[x]);
return father[x];
}
inline void hebing(int x,int y){
father[y]=x;
}
inline void dfs(int x,int deep){
height[x]=deep;
for(int i=1;i<=15;i++){
f[x][i]=f[ f[x][i-1] ][i-1];
quan[x][i]=max( quan[x][i-1],quan[ f[x][i-1] ][i-1] );
}
for(int i=first[x];i;i=next[i]){
if(height[to1[i]]==0)
{
f[ to1[i] ][0]=x;
quan[ to1[i] ][0]=ww[i];
dfs(to1[i],deep+1);
}
}
}
int lca(int x,int y){
if(height[x]<height[y]) { int t=x;x=y;y=t; }
int t=0;
while((1<<t) <=height[x]) t++;
t--;
int ans1=-0x7ffffff,ans2=-0x7ffffff;
for(int i=t;i>=0;i--){
if(height[x]-(1<<i)>=height[y]) {
ans1=max(ans1,quan[x][i]);
x=f[x][i];
}
}
if(x==y) return ans1;
for(int i=t;i>=0;i--){
if(f[x][i]!=f[y][i]){
ans1=max(ans1,quan[x][i]); ans2=max(ans2,quan[y][i]);
x=f[x][i];y=f[y][i];
}
}
int zong1,zong2;
zong1=max(ans1,quan[x][0]);
zong2=max(ans2,quan[y][0]);
return max(zong1,zong2);
}
inline void work(){
qsort(1,m);
for(int i=1;i<=n;i++) father[i]=i;
int i=1,j=0;
int yigong=0;
while(i<=m){
int r1=find(u[i]);int r2=find(to[i]);
hebing(r1,r2);
yigong++;
j++; next[j]=first[u[i]]; first[u[i]]=j;ww[j]=w[i]; to1[j]=to[i]; u1[j]=u[i];
j++; next[j]=first[to[i]]; first[to[i]]=j;ww[j]=w[i]; to1[j]=u[i]; u1[j]=to[i];
i++;
while(find(u[i])==find(to[i]) && i<=m)
i++;
}
for(int i=1;i<=n;i++)
if(father[i]==i)
{
dfs(i,1);
}
}
int main()
{
n=getint();m=getint();int q=getint();
int ljh,jump,jumpjump;
for(int i=1;i<=m;i++){
ljh=getint();jump=getint();jumpjump=getint();
u[i]=ljh;to[i]=jump;w[i]=jumpjump;
}
work();
for(int i=1;i<=q;i++){
ljh=getint();jump=getint();
int ans=lca(ljh,jump);
printf("%d\n",ans);
}
return 0;
}
#include<cctype>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 45005
#define F inline
using namespace std;
struct edge{ int x,y,z; }ed[N];
int n,m,k,q,nd,f[N],dep[N],fa[N][18],t[N][2],w[N];
F char readc(){
static char buf[100000],*l=buf,*r=buf;
if (l==r) r=(l=buf)+fread(buf,1,100000,stdin);
return l==r?EOF:*l++;
}
F int _read(){
int x=0; char ch=readc();
while (!isdigit(ch)) ch=readc();
while (isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=readc();
return x;
}
F void writec(int x){ if (x>9) writec(x/10); putchar(x%10+48); }
F void _write(int x){ writec(x),puts(""); }
F bool cmp(edge a,edge b){ return a.z<b.z; }
int findfa(int x){ return x==f[x]?x:f[x]=findfa(f[x]); }
void dfs(int x){
if (!x) return; dep[x]=dep[fa[x][0]]+1;
dfs(t[x][0]),dfs(t[x][1]);
}
F void Make(){
for (int j=1;j<18;j++)
for (int i=1;i<n<<1;i++)
fa[i][j]=fa[fa[i][j-1]][j-1];
}
F int LCA(int x,int y){
if (dep[x]<dep[y]) swap(x,y);
for (int j=17;~j;j--)
if (dep[fa[x][j]]>=dep[y]) x=fa[x][j];
if (x==y) return x;
for (int j=17;~j;j--)
if (fa[x][j]!=fa[y][j])
x=fa[x][j],y=fa[y][j];
return fa[x][0];
}
int main(){
nd=n=_read(),m=_read(),q=_read();
for (int i=1,x,y;i<=m;i++)
x=_read(),y=_read(),ed[++k]=(edge){x,y,_read()};
sort(ed+1,ed+m+1,cmp);
for (int i=1;i<n<<1;i++) f[i]=i;
for (int i=1,s=0,x,y,fx,fy;s<n-1;i++)
if ((fx=findfa(x=ed[i].x))!=(fy=findfa(y=ed[i].y))){
t[++nd][0]=fx,t[nd][1]=fy,w[nd]=ed[i].z;
f[fx]=f[fy]=fa[fx][0]=fa[fy][0]=nd,s++;
}
for (dfs(nd),Make();q;q--) _write(w[LCA(_read(),_read())]);
return 0;
}
//https://blog.csdn.net/a1799342217/article/details/81366780
路径权值
Description
给定一个带权树,树上任意两点间的路径权值d(x,y)定义为x,y这两个点之间路径上的最小值,
树上任意一点x的权值定义为这个点到树上其他所有点的路径权值和,
即Sigma(d(x,i)),1<=i<=N,现求树上一点,使得这个点的权值最大,输出这个值。
Input
首先输入一个整数Q,接着每组数据首先输入一个整数 n(1≤n≤100000),
表示该组数据中树的点的个数。
接下来n-1行,每行三个整数 x,y,s(1≤x,y≤n,1≤s≤1000),
表示编号为x的节点和编号为y的节点之间存在一条权值为s的边,树上每个点的编号为1 n
Output
对于每组数据,首先输出数据编号,然后输出树上的点的最大权值,具体格式见输出样例。
Sample Input
2
4
1 2 2
2 4 1
2 3 1
4
1 2 1
2 4 1
2 3 1
Sample Output
Case 1: 4
Case 2: 3
这道题目怎么做呢?
显然,如果我们暴力枚举点对是不可行的。
既然是和树上路径有关的问题,点分治可不可行呢?
本蒟蒻太菜了,根本想不到啊qwq
那我们试图算一下边的贡献,即一条边对所有经过这一条边的点对都会有这条边长度的贡献。
怎么算呢?
我们之前提到过Kruskal重构树中,两个节点的LCA节点就是两点路径上的最大/最小节点。
也就是说,对于一个非叶节点x,
它左子树中的节点到右子树中的节点的路径一定会经过x节点所对应的边,反之亦然。
那么我们就可以建出Kruskal重构树之后维护当前边对于重构树子树中节点的贡献了。
这个区间加法的过程我们可以用树状数组实现。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int Maxn=100005;
inline int read() {
static char c; int rec=0;
while((c=getchar())<'0'||c>'9');
while(c>='0'&&c<='9') rec=rec*10+c-'0',c=getchar();
return rec;
}
int T,n;
struct Edge {int a,b,w;} e[Maxn];
inline bool operator < (const Edge &A,const Edge &B) {return A.w>B.w;}
struct Branch {int next,to;} branch[Maxn<<1];
int h[Maxn<<1],cnt=0;
inline void add(int x,int y) {
branch[++cnt].to=y; branch[cnt].next=h[x]; h[x]=cnt; return ;
}
int fa[Maxn<<1],val[Maxn<<1];
inline int getfa(int x) {return x==fa[x]?x:fa[x]=getfa(fa[x]);}
inline void Ex_Kruskal() {
int ind=n,lim=n<<1; sort(e+1,e+n);
for(int i=1;i<lim;++i) fa[i]=i;
for(int i=1;i<n;++i) {
int fx=getfa(e[i].a),fy=getfa(e[i].b);
fa[fx]=fa[fy]=++ind;
val[ind]=e[i].w;
add(ind,fx); add(ind,fy);
} return ;
}
int size[Maxn<<1],st[Maxn<<1],ed[Maxn<<1],idx;
inline void Dfs(int v) {
size[v]=v<=n; st[v]=++idx;
for(int i=h[v];i;i=branch[i].next)
Dfs(branch[i].to),size[v]+=size[branch[i].to];
ed[v]=idx;
}
struct Bit {
int c[Maxn<<1];
inline void reset(){memset(c,0,n<<3); return ;}
inline void Insert(int x,int d) {while(x<=n<<1) c[x]+=d,x+=x&-x; return ;}
inline int Ask(int x) {int rec=0; while(x>=1) rec+=c[x],x-=x&-x; return rec;}
}A;
int main() {
T=read();
for(int t=1;t<=T;++t) {
cnt=0; idx=0; memset(h,0,4*(n<<1));
n=read();
for(int i=1;i<n;++i) {
int x=read(),y=read(),z=read();
e[i]=(Edge){x,y,z};
}
Ex_Kruskal(); Dfs((n<<1)-1);
A.reset();
for(int i=n+1;i<n<<1;++i) {
int ls=0,rs;
for(int k=h[i];k;k=branch[k].next) {
if(ls) rs=branch[k].to;
else ls=branch[k].to;
}
A.Insert(st[ls],val[i]*size[rs]);
A.Insert(ed[ls]+1,-val[i]*size[rs]);
A.Insert(st[rs],val[i]*size[ls]);
A.Insert(ed[rs]+1,-val[i]*size[ls]);
}
int ans=0;
for(int i=1;i<=n;++i) ans=max(ans,A.Ask(st[i]));
cout<<"Case "<<t<<": "<<ans<<'\n';
}
return 0;
}
//https://blog.csdn.net/hwzzyr/article/details/81190442
最后要提到的就是我们Kruskal重构树最常见的经典题目
【BZOJ3551】Peaks加强版
Description
在Bytemountains有N座山峰,每座山峰有他的高度h_i。有些山峰之间有双向道路相连,共M条路径,每条路径有一个困难值,这个值越大表示越难走,现在有Q组询问,每组询问询问从点v开始只经过困难值小于等于x的路径所能到达的山峰中第k高的山峰,如果无解输出-1。
Input
第一行三个数N,M,Q。
第二行N个数,第i个数为h_i
接下来M行,每行3个数a b c,表示从a到b有一条困难值为c的双向路径。
接下来Q行,每行三个数v x k,表示一组询问。v=v xor lastans,x=x xor lastans,k=k xor lastans。如果lastans=-1则不变。
Output
对于每组询问,输出一个整数表示答案。
Sample Input
10 11 4
1 2 3 4 5 6 7 8 9 10
1 4 4
2 5 3
9 8 2
7 8 10
7 1 4
6 7 1
6 4 8
2 1 5
10 8 10
3 4 7
3 4 6
1 5 2
1 5 6
1 5 8
8 9 2
Sample Output
6
1
-1
8
Hint
【数据范围】
N<=10^5, M,Q<=5*10^5,h_i,c,x<=10^9。
显然,我们题目中“边权小于等于x”的限制条件我们在Kruskal重构树上就变成了一个深度限制。
对于询问节点的祖先,如果祖先节点的权值是不超过x的,那么这颗子树中的所有节点我们都可以到达。
问题就转化成为了静态子树中的权值第k大,可以用可持久化线段树解决。
https://blog.csdn.net/hwzzyr/article/details/81190442
#include<bits/stdc++.h>
using namespace std;
const int Maxn=200005;
const int Maxm=500005;
inline int read() {
static char c; int rec=0;
while((c=getchar())<'0'||c>'9');
while(c>='0'&&c<='9') rec=rec*10+c-'0',c=getchar();
return rec;
}
int n,m,Q,N,last;
int val[Maxn<<1],table[Maxn];
int fa[Maxn<<1],st[Maxn],ed[Maxn];
inline int getfa(int x) {return x==fa[x]?x:fa[x]=getfa(fa[x]);}
struct Edge {int a,b,w;} e[Maxm];
inline bool operator < (const Edge &A,const Edge &B) {return A.w<B.w;}
namespace Sgt {
int cnt=0,root[Maxn<<1];
#define mid ((L+R)>>1)
struct Dynamic_Segment_Tree {int s[2],d;} tree[Maxn*20];
inline void Infix(int &v,int p,int L,int R,int x) {
v=++cnt; tree[v]=tree[p]; ++tree[v].d;
if(L==R) return ;
int f=(x>mid); f?L=mid+1:R=mid;
Infix(tree[v].s[f],tree[p].s[f],L,R,x);
return ;
}
inline int Ask(int x,int y,int L,int R,int k) {
if(L==R) return L;
int sum=tree[tree[y].s[1]].d-tree[tree[x].s[1]].d;
if(sum>=k) return Ask(tree[x].s[1],tree[y].s[1],mid+1,R,k);
else return Ask(tree[x].s[0],tree[y].s[0],L,mid,k-sum);
}
}
struct Branch {int next,to;} branch[Maxn<<1];
int h[Maxn<<1],cnt=0;
inline void add(int x,int y) {
branch[++cnt].to=y; branch[cnt].next=h[x]; h[x]=cnt; return ;
}
void Ex_Kruskal() {
int ind=n; sort(e+1,e+1+m);
for(int i=1;i<=m;++i) {
int fx=getfa(e[i].a),fy=getfa(e[i].b);
if(fx!=fy) {
fa[fx]=fa[fy]=++ind;
val[ind]=e[i].w;
add(ind,fx); add(ind,fy);
if(ind==2*n-1) break;
}
} return ;
}
int idx=0;
int F[Maxn][18],deep[Maxn];
inline void Dfs(int v) {
deep[v]=deep[F[v][0]]+1; st[v]=++idx;
for(int i=1;i<18;++i)
if(deep[v]<(1<<i)) break;
else F[v][i]=F[F[v][i-1]][i-1];
if(v<=n) Sgt::Infix(Sgt::root[idx],Sgt::root[idx-1],1,N,val[v]);
else Sgt::root[idx]=Sgt::root[idx-1];
for(int i=h[v];i;i=branch[i].next) {
int j=branch[i].to;
F[j][0]=v; Dfs(j);
}
ed[v]=idx; return ;
}
inline void Find_Pos(int &v,int lim) {
for(int i=17;~i;--i) {
if(deep[v]<(1<<i)) continue;
if(val[F[v][i]]<=lim) v=F[v][i];
} return ;
}
int main() {
n=read(); m=read(); Q=read(); val[0]=0x3f3f3f3f;
for(int i=1;i<=n;++i) table[i]=val[i]=read();
sort(table+1,table+1+n); N=unique(table+1,table+1+n)-table-1;
for(int i=1;i<=n;++i) val[i]=lower_bound(table+1,table+1+N,val[i])-table;
for(int i=1;i<=(n<<1);++i) fa[i]=i;
for(int i=1;i<=m;++i) {
int a=read(),b=read(),w=read();
e[i]=(Edge){a,b,w};
}
Ex_Kruskal();
for(int i=1;i<=n;++i) if(!st[i]) Dfs(getfa(i));
for(int i=1;i<=Q;++i) {
int v=read()^last,x=read()^last,k=read()^last;
Find_Pos(v,x);
if(Sgt::tree[Sgt::root[ed[v]]].d-Sgt::tree[Sgt::root[st[v]-1]].d<k) last=-1;
else last=table[Sgt::Ask(Sgt::root[st[v]-1],Sgt::root[ed[v]],1,N,k)];
cout<<last<<'\n';
last=last<0?0:last;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号