P2633 Count on a tree

给定一棵 n 个节点的树，每个点有一个权值。有 m 个询问，每次给你 u,v,k，你需要回答u xor last 和 v 这两个节点间第 k 小的点权。

其中 last 是上一个询问的答案，定义其初始为 0，即第一个询问的 u 是明文。

输入格式
第一行两个整数 n,m

第二行有 n 个整数，其中第 i个整数表示点 i 的权值。

后面 n-1行每行两个整数 x,y表示点 x 到点 y有一条边。

最后 m行每行两个整数 u,v,k表示一组询问。

输出格式
m行，每行一个正整数表示每个询问的答案。

input
8 5
105 2 9 3 8 5 7 7
1 2
1 3
1 4
3 5
3 6
3 7
4 8
2 5 1
0 5 2
10 5 3
11 5 4
110 8 2

output

2
8
9
105
7

1≤n,m≤1E5

Sol:建立主席树，第i个主席树为，从根到i这一条链上的信息。
于是询问x,y这一条链上的第K大问题，就变成了第x棵树的信息+第Y棵树的-第Lca(x,y)-第father(lca(x,y))

 

 

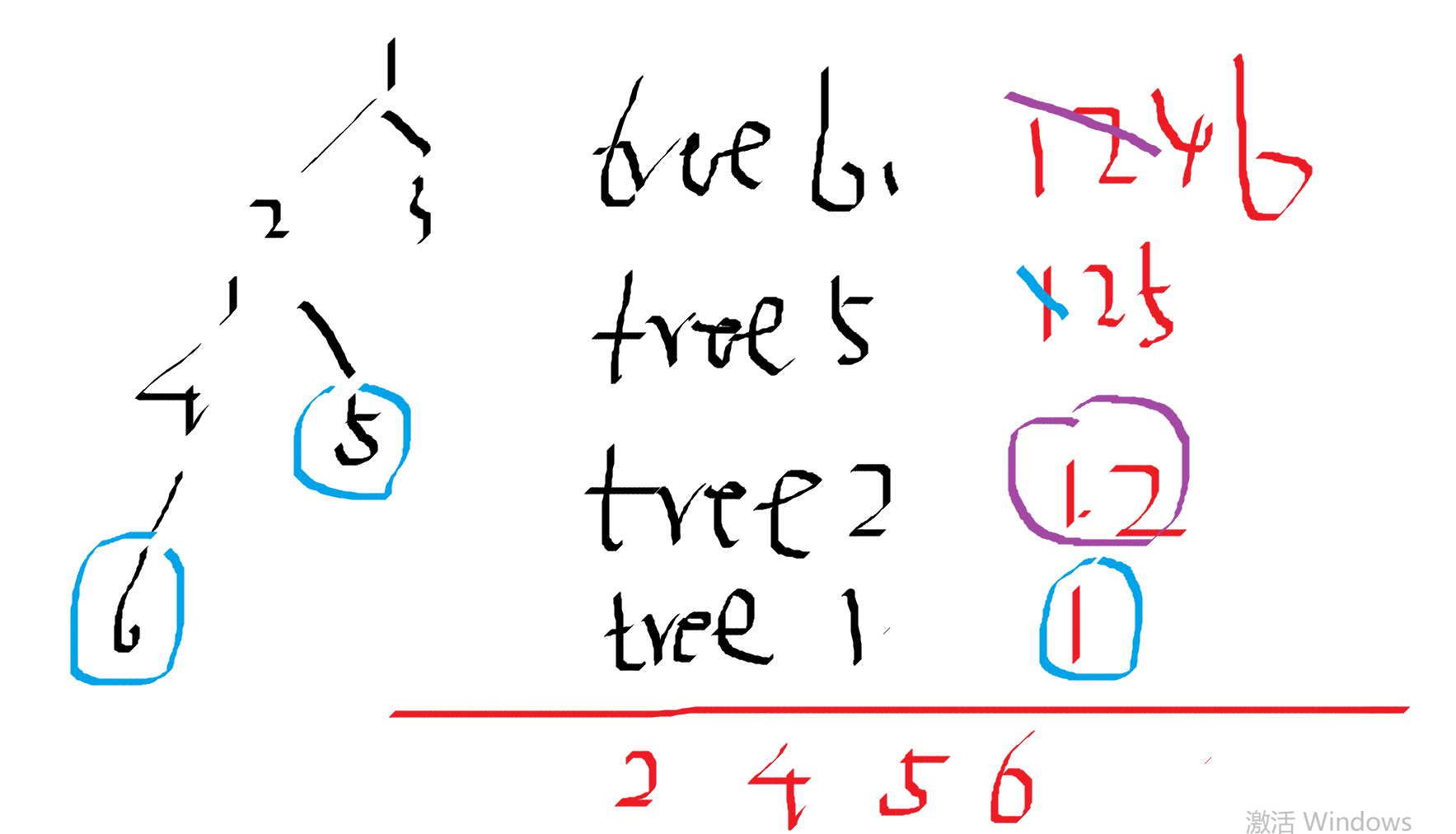
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#define ll long long
using namespace std;
const int N = 2e5+5;
int root[N], cnt;
int lisan[N];
int su[N];
int mx;
int tot = 1;
int he[N], ne[N<<1], ver[N<<1];
int f[N][20];
int dep[N];
void add(int x, int y)
{
    ne[++tot] = he[x];
    ver[tot] = y;
    he[x] = tot;
}
struct Node
{
    int l, r, sum;
}tr[N<<5];
inline int getn(int g)
{
    return lower_bound(lisan+1, lisan+mx, g) - lisan;
}
void change(int l, int r, int &p, int pre, int v)
{
    tr[++cnt] = tr[pre];
    p = cnt;
    tr[p].sum++;
    if (l == r) 
	    return;
    int mid = (l+r) >>1;
    if (v <= mid) 
	    change(l, mid, tr[p].l, tr[pre].l, v);
    else 
	    change(mid+1, r,tr[p].r, tr[pre].r, v);
}
void dfs(int u, int fa)
{
    change(1, mx-1, root[u], root[fa], getn(su[u]));
    f[u][0] = fa;
    dep[u] = dep[fa] + 1;
    for (int i = 1; i <= 18; i++)
        f[u][i] = f[f[u][i-1]][i-1];
    for (int i = he[u]; i; i = ne[i])
    {
        int y = ver[i];
        if (y == fa) continue;
        dfs(y, u);
    }
}
int lca(int x, int y)
{
    if (dep[x] > dep[y]) 
	    swap(x, y);
    for (int i = 18; i >= 0; i--)
    {
        if (dep[f[y][i]] < dep[x]) continue;
        y = f[y][i];
    }
    if (x == y) 
	    return x;
    for (int i = 18; i >= 0; i--)
        if (f[x][i] != f[y][i]) 
		    x = f[x][i], y = f[y][i];
    return f[x][0];
}
int ask(int l, int r, int x, int y, int z, int w, int k)
{
    if (l == r) 
	    return l;
    int sum = tr[tr[x].l].sum + tr[tr[y].l].sum - tr[tr[z].l].sum - tr[tr[w].l].sum;
    int mid = (l + r) >> 1;
    if (sum >= k) 
	    return ask(l, mid, tr[x].l, tr[y].l, tr[z].l, tr[w].l, k);
    return 
	     ask(mid+1, r, tr[x].r, tr[y].r, tr[z].r, tr[w].r, k-sum);
}
int mask(int x, int y, int k)
{
    int _lca = lca(x, y);
    return lisan[ask(1, mx-1, root[x], root[y], root[_lca], root[f[_lca][0]], k)];
}
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &su[i]);
        lisan[++mx] = su[i];
    }
    sort(lisan+1, lisan+mx+1);
    mx = unique(lisan+1, lisan+mx+1) - lisan;
    for (int i= 1; i < n; i++)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        add(x, y); 
		add(y, x);
    }
    dfs(1, 0);
    int la = 0;
    while(m--)
    {
        int x, y, k;
        scanf("%d%d%d", &x, &y, &k);
        printf("%d\n", la = mask(x^la, y, k));
    }
    return 0;
}

//https://blog.csdn.net/qq_35802619/article/details/101717621

　　

 

如果变成带修改的话

[BZOJ1146][CTSC2008]网络管理Network（树状数组套线段树）

 

https://blog.csdn.net/xyz32768/article/details/81458418?utm_medium=distribute.pc_relevant.none-task-blog-2~default~BlogCommendFromBaidu~default-2.control&dist_request_id=&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~BlogCommendFromBaidu~default-2.control