splay的区间平移与翻转操作
Hdu 3487 play the chain
瑶瑶很喜欢玩项链,她有一根项链上面有很多宝石,宝石从1到n编号。
首先,项链上的宝石的编号组成一个序列:1,2,3,...,n。
她喜欢两种操作:
1.CUT a b c:他会先将a至b号宝石切下来,然后接到c号宝石后面,组成一个新的项链。
举个例子,如果n=8,那么这个项链上的宝石编号依次为:1 2 3 4 5 6 7 8;'CUT 3 5 4',首先我们把3到5号宝石切下
项链变成了:1 2 6 7 8;然后接到4号宝石后面,此时的4号宝石为7,所以此时的项链变成了:1 2 6 7 3 4 5 8.
2.FLIP a b:像第一个操作一样我们先将a至b号宝石切下来,然后将其旋转180°,变成与原来相反的链,在插入到项链的相 同位置中。
举个例子,取操作1中的链:1 2 3 4 5 6 7 8,执行FLIP 2 6操作,则项链将变成:1 6 5 4 3 2 7 8.
他想知道经过m个操作之后项链会变成怎样。
输入
对于每一个数据,第一行会有两个整数:n m(1<=n,m<=300000) n代表宝石的个数,m代表操作的个数。
接下来有M行 有两个操作:
CUT A B C //代表CUT操作,1<=A<=B<=N, 0<=C<=N-(B-A+1).
FLIP A B //代表FLIP操作,1<=A<=B<=N.
输出的结尾将会有两个负数,他们不能当做操作.
输出
对于每一个数据,你需要输出N个整数,任两个数字间用一个空格分开,代表最终得到的项链的从1到N的宝石的序列号。
样例输入
8 2
CUT 3 5 4
FLIP 2 6
-1 -1
样例输出
1 4 3 7 6 2 5 8
将1,2,3,4,5,6,7,8中的3,4移到6的后面,7的前面
设a=3,b=5,c=7.
原图为
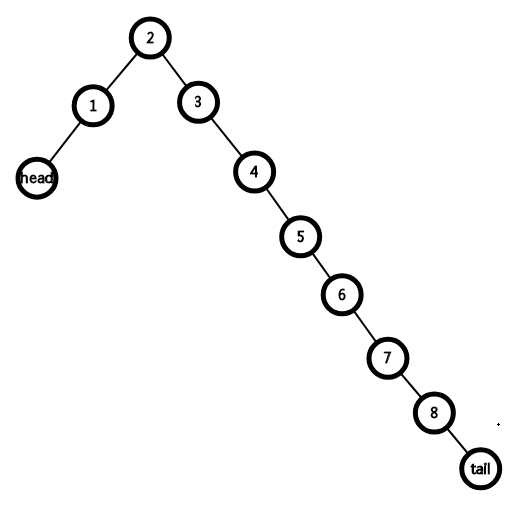
先将a=3旋转为根,此为定好开始点,得到
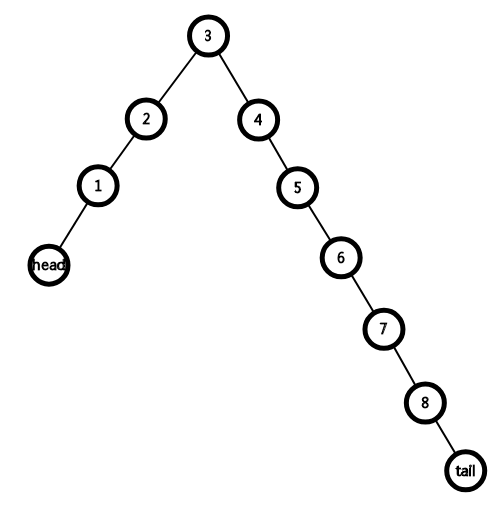
再将b=5旋转为根,此为定好结束点,目标区域为[a,b)这一段,得到

发现3现在的父亲不是5,于是将3旋转一次,得到

此时我们的目标区域已出来,在以3为根的树及其右子树,于是将其拿出来。将3的左子树直接连成5的左子树(因为3的左子树在今后的中序遍历中,要先于5访问),然后找到c=7这个点,变成7的左子树。如果此时7的左子树不为空,则将其变为3的左子树(理由如下,目标区域要先于7访问)
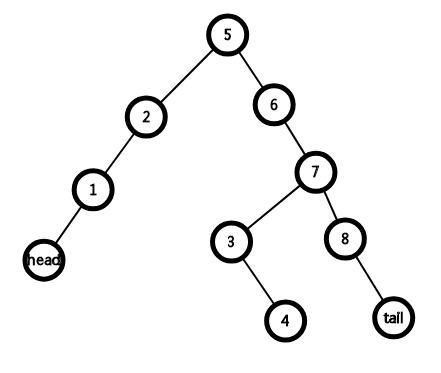
如果是将1 2 5 6 3 4 7 8中的5移到2的前面,变成1 5 2 6 3 4 7 8,则进行图如下
原图为:

先变成:

拿出以5为根及其右子树(此时为空)
将其做为2的左子树,2从前的左子树变成5的左子树,得到
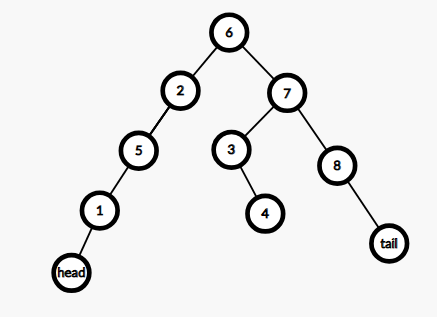
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read()
{
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
inline void print(int x)
{
if (x>=10) print(x/10);
putchar(x%10+'0');
}
const int N=3e5;
int n,m;
struct Splay
{
#define T(x) (tree[f[x]][1]==x)
int tree[N+10][2],f[N+10],size[N+10];
bool flag[N+10];
int root,cnt;
void clear()
{
root=cnt=0;
memset(f,0,sizeof(f));
memset(tree,0,sizeof(tree));
memset(size,0,sizeof(size));
memset(flag,0,sizeof(flag));
}
void pushdown(int x)
{
if (!flag[x]) return;
swap(tree[x][0],tree[x][1]);
flag[tree[x][0]]^=1;
flag[tree[x][1]]^=1;
flag[x]=0;
}
void write(int x)
{
if (!x) return;
pushdown(x);
write(tree[x][0]);
if (x<=n) ++cnt!=n?printf("%d ",x):printf("%d\n",x);
write(tree[x][1]);
}
void build()
{
root=n+1;
for (int i=1;i<=n;i++)
f[i]=i+1,size[i]=i+1,tree[i+1][0]=i;
//建立一条链出来,1在最下面,n在最上面
f[n+2]=1,size[n+2]=1,tree[1][0]=n+2;
//1的左子树挂一个节点
size[root]=n+2;
}
void updata(int x)
{
size[x]=size[tree[x][0]]+size[tree[x][1]]+1;
}
void move(int x) //一次旋转操作
{
int fa=f[x],son=tree[x][T(x)^1];
tree[x][T(x)^1]=fa;
tree[fa][T(x)]=son;
if (son)
f[son]=fa;
f[x]=f[fa];
if (f[x])
tree[f[x]][T(fa)]=x;
f[fa]=x;
updata(fa),updata(x);
}
void splay(int x) //将x变成根
{
while (f[x])
{
if (f[f[x]])
T(x)==T(f[x])?move(f[x]):move(x);
move(x);
}
root=x;
}
int find(int x,int i)
{
if (!i) return 0;
pushdown(i);
if (size[tree[i][0]]+1==x)
return i;
if (x<=size[tree[i][0]])
return find(x,tree[i][0]);
return
find(x-size[tree[i][0]]-1,tree[i][1]);
}
void flip()
{
int x=read(),y=read();
x=find(x,root),splay(x);
//x为我们要翻转区间的前一个数字
//我们要以x为根,将目标区域变成其右子树,
//这个与cut操作稍有不同。因为翻转时涉及到标记下传
//所以应该将所有结点做成一棵整个的树,
//cut的时候是进行移动,移动就需要从一个开始点开始进行
//于是让这个开始点做为根,所以其它结点做为其右子树。
//对于文章中的配图,就是将[4,4]这一段翻转
y=find(y+2,root),splay(y);
if (f[x]!=root)
move(x);
//以上为挖出所要区间来
flag[tree[x][1]]^=1;
}
void consert(int x,int fa)
//如果x是fa的子结点的话,则cut之
//否则就将x变成fa的左子结点
{
if (tree[f[x]][T(x)]==x)
tree[f[x]][T(x)]=0;
f[tree[fa][0]=x]=fa;
}
void up(int x)
{
while (f[x])
updata(x),x=f[x];
}
void cut()
{
//1,2,3,4,5,6,7,8
//把[3,4]放到6后面
int x=read(),y=read(),z=read();
//x=3,y=4,z=6
//注意前面开了一个空结点
x=find(x+1,root),splay(x);//x=3
y=find(y+2,root),splay(y);//y=5,也就是找到[3,4]后面那个点
if (f[x]!=root)
//如果3的父亲不是根,就要旋转一次
move(x);
consert(tree[x][0],f[x]);
//将3的左子结点变为5的左子结点
//以3为根的(含右子树)拿出来
z=find(z+2,root);// 找到6后面那个点7
consert(tree[z][0],x);//将7的左子结点变为3的左子结点
consert(x,z);//将3变为7的左子结点
up(x);//更新节点信息
}
}T;
char s[10];
int main(){
while (1){
T.clear();
n=read(),m=read();
if (n==-1&&m==-1) break;
T.build();
for (int i=1;i<=m;i++)
{
scanf("%s",s);
if (s[0]=='F') T.flip();
if (s[0]=='C') T.cut();
}
T.write(T.root);
}
return 0;
}
序列终结者
给定一个长度为N的序列,每个序列的元素是一个整数(废话)。
要支持以下三种操作:
将[L,R]这个区间内的所有数加上V。
将[L,R]这个区间翻转,比如1 2 3 4变成4 3 2 1。
求[L,R]这个区间中的最大值。 最开始所有元素都是0。
输入
第一行两个整数N,M。M为操作个数。
以下M行,每行最多四个整数,依次为K,L,R,V。K表示是第几种操作,如果不是第1种操作则K后面只有两个数。
输出
对于每个第3种操作,给出正确的回答。
样例
输入
4 4
1 1 3 2
1 2 4 -1
2 1 3
3 2 4
输出
2
#include<cstdio>
#include<algorithm>
#include<cstring>
#define p(x) (s[fa[x]][1]==x)
using namespace std;
const int maxn=50010;
int n,m,root,summin,summax;
int fa[maxn],s[maxn][2],v[maxn],siz[maxn],v_max[maxn],lazy_flip[maxn],lazy_sum[maxn];
int read()
{
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*f;
}
void pushdown(int x)
{
if (lazy_sum[x])
{
if (s[x][0])
v[s[x][0]]+=lazy_sum[x],
v_max[s[x][0]]+=lazy_sum[x],
lazy_sum[s[x][0]]+=lazy_sum[x];
if (s[x][1])
v[s[x][1]]+=lazy_sum[x],
v_max[s[x][1]]+=lazy_sum[x],
lazy_sum[s[x][1]]+=lazy_sum[x];
lazy_sum[x]=0;
}
if (lazy_flip[x])
{
swap(s[x][0],s[x][1]);
if (s[x][0])
lazy_flip[s[x][0]]^=1;
if (s[x][1])
lazy_flip[s[x][1]]^=1;
lazy_flip[x]=0;
}
}
void updata(int x)
{
siz[x]=siz[s[x][0]]+siz[s[x][1]]+1;
v_max[x]=v[x];
if (s[x][0])
v_max[x]=max(v_max[x],v_max[s[x][0]]);
if (s[x][1])
v_max[x]=max(v_max[x],v_max[s[x][1]]);
}
void move(int x)
{
int f=fa[x],t=p(x),son=s[x][1-t];
s[f][t]=son;
if (son) fa[son]=f;
fa[x]=fa[f];
if (fa[f]) s[fa[f]][p(f)]=x;
fa[f]=x;
s[x][1-t]=f;
updata(f),updata(x);
}
void splay(int x,int f)
//将x旋转成为f的子结点
{
while(fa[x]!=f)
{
if (fa[fa[x]]!=f)
{
if (p(x)==p(fa[x])) move(fa[x]);
else move(x);
}
move(x);
}
if (!f) root=x;
return;
}
int find(int x,int k)
{
pushdown(x);
if (siz[s[x][0]]+1==k) return x;
if (siz[s[x][0]]>=k) return find(s[x][0],k);
return find(s[x][1],k-siz[s[x][0]]-1);
}
void build(int l,int r,int f,int t)
//对于区间[l,r]其父亲点是f,t代表是上一个区间的左边还是右边
{
if (l>r) return;
int mid=(l+r)>>1;
siz[mid]=1;
fa[mid]=f;
if (f)
//f不为0时,f结点的t儿子为mid点
s[f][t]=mid;
else
//否则设mid为root点,mid的父亲点为0号点
root=mid;
build(l,mid-1,mid,0),build(mid+1,r,mid,1);
siz[mid]+=siz[s[mid][0]]+siz[s[mid][1]];
return;
}
int main()
{
n=read(),m=read();
build(1,n+2,0,0);
//开始时数列为空!!!,最前面及最后面加一个空结点
for (int i=1;i<=m;i++)
{
int k=read(),l=read(),r=read(),sl=find(root,l),sr=find(root,r+2);
// 原数列 1, 2, 3, 4, 5, 6, 7, 8
// | | | | | | | |
//新数列 2, 3, 4, 5, 6, 7, 8, 9
splay(sl,0);
//因为前面有个空结点,所以sl其实为l左边那个点,将sl做为根结点
splay(sr,sl);
//sr做为sl的右子结点
//sr为从前r右边的那个点
if (k==1)
{
int sum=read();
v_max[s[sr][0]]+=sum;
//目标区域为sr的左子树
v[s[sr][0]]+=sum;
lazy_sum[s[sr][0]]+=sum;
}
if (k==2) lazy_flip[s[sr][0]]^=1;
if (k==3) printf("%d\n",v_max[s[sr][0]]);
}
return 0;
}
/*
目标区间为[x,y],将x前面一个位置a先旋成根
再将y后面那个位置b旋转成根
再让a做为b的左子点
于是目标区域就是x的右子树了
当然也可以让a做root
b做为a的右子结点
目标区域为b的左子结点
*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
inline void print(int x){
if (x>=10) print(x/10);
putchar(x%10+'0');
}
const int N=5e4;
struct Splay
{
#define T(x) (tree[f[x]][1]==x)
#define ls(x) tree[x][0]
#define rs(x) tree[x][1]
int tree[N+10][2],size[N+10],f[N+10],val[N+10],cnt[N+10],Max[N+10];
bool rev[N+10];
int root,len;
void build(int n)
{
root=n+1;
for (int i=1;i<=n;i++)
f[i]=size[i]=i+1,ls(i+1)=i;
f[ls(1)=n+2]=1,Max[n+2]=val[n+2]=-inf,size[n+2]=1;
size[root]=n+2,Max[root]=val[root]=inf;
}
void Rev(int x)
{
swap(ls(x),rs(x));
rev[ls(x)]^=1,rev[rs(x)]^=1;
rev[x]=0;
}
void Inc(int x)
{
cnt[ls(x)]+=cnt[x],Max[ls(x)]+=cnt[x],val[ls(x)]+=cnt[x];
cnt[rs(x)]+=cnt[x],Max[rs(x)]+=cnt[x],val[rs(x)]+=cnt[x];
cnt[x]=0;
}
void pushdown(int x)
{
if (rev[x]) Rev(x);
if (cnt[x]) Inc(x);
}
void updata(int x)
{
size[x]=size[ls(x)]+size[rs(x)]+1;
Max[x]=val[x];
if (ls(x))
Max[x]=max(Max[x],Max[ls(x)]);
if (rs(x))
Max[x]=max(Max[x],Max[rs(x)]);
}
void move(int x)
{
int fa=f[x],son=tree[x][T(x)^1];
tree[x][T(x)^1]=fa;
tree[fa][T(x)]=son;
if (son)
f[son]=fa;
f[x]=f[fa];
if (f[x])
tree[f[x]][T(fa)]=x;
f[fa]=x;
updata(fa),updata(x);
}
void up(int x)
{
if (!x) return;
up(f[x]);
pushdown(x);
}
void splay(int x)
{
// up(x);
while (f[x])
{
if (f[f[x]])
T(x)==T(f[x])?move(f[x]):move(x);
move(x);
}
root=x;
}
int find(int x,int i)
{
pushdown(i);
if (size[ls(i)]+1==x)
return i;
if (x<=size[ls(i)])
return find(x,ls(i));
return
find(x-size[ls(i)]-1,rs(i));
}
void ADD(int x,int y,int v)
//目标区间为[x,y],将x前面一个位置先旋成根
//再将y后面那个位置旋转成根
//再让x做为y的左子点
//于是目标区域就是x的右子树了
{
x=find(x,root),splay(x);
y=find(y+2,root),splay(y);
if (f[x]!=root)
move(x);
cnt[rs(x)]+=v;
Max[rs(x)]+=v;
val[rs(x)]+=v;
}
void filp(int x,int y)
{
x=find(x,root),splay(x);
y=find(y+2,root),splay(y);
if (f[x]!=root)
move(x);
rev[rs(x)]^=1;
}
void query(int x,int y){
x=find(x,root),splay(x);
y=find(y+2,root),splay(y);
if (f[x]!=root) move(x);
printf("%d\n",Max[rs(x)]);
}
}T;
int main(){
int n=read(),m=read();
T.build(n);
for (int i=1;i<=m;i++){
int k=read(),x=read(),y=read();
if (k==1) T.ADD(x,y,read());
if (k==2) T.filp(x,y);
if (k==3) T.query(x,y);
}
return 0;
}
在建立splay树时,为了更均衡点,可以采用类似线段树的方式,例如有10个结点时:

#include<bits/stdc++.h>
using namespace std;
#define maxn 100050
int n,ch[maxn][2],f[maxn],size[maxn],num[maxn];
int root,sz,rev[maxn],add[maxn],mx[maxn],m;
struct node{
int s,id;
}a[maxn];
int p[maxn];
void read(int &x) {
char ch; bool ok;
for(ok=0,ch=getchar(); !isdigit(ch); ch=getchar()) if(ch=='-') ok=1;
for(x=0; isdigit(ch); x=x*10+ch-'0',ch=getchar()); if(ok) x=-x;
}
void pushdown(int x)
{
int l=ch[x][0],r=ch[x][1];
if(rev[x])
{
rev[l]^=1;rev[r]^=1;
swap(ch[x][0],ch[x][1]);
rev[x]=0;
}
if(add[x])
{
int ad=add[x];
if(l) num[l]+=ad,mx[l]+=ad,add[l]+=ad;
if(r) num[r]+=ad,mx[r]+=ad,add[r]+=ad;
add[x]=0;
}
}
void update(int x)
{
size[x]=1+size[ch[x][0]]+size[ch[x][1]];
mx[x]=max(max(mx[ch[x][1]],mx[ch[x][0]]),num[x]);
}
inline void rotate(int &k,int x)
{
int y=f[x],z=f[y],l,r;
if(ch[y][0]==x) l=0;
else l=1;
r=l^1;
if(k==y) k=x;
else
{
if(ch[z][0]==y) ch[z][0]=x;
else ch[z][1]=x;
}
f[x]=z;f[y]=x;f[ch[x][r]]=y;
ch[y][l]=ch[x][r];ch[x][r]=y;
update(y);update(x);
}
inline void splay(int &k,int x)
{
while(x!=k)
{
int y=f[x],z=f[y];
if(y!=k)
{
if((ch[y][0]==x)^(ch[z][0]==y))
rotate(k,x);
else
rotate(k,y);
}
rotate(k,x);
}
}
inline void build(int l,int r,int last)
{
if (l>r) return;
if (l==r)
{
f[l]=last;
size[l]=1;
if(l<last)
ch[last][0]=l;
else
ch[last][1]=l;
return;
}
int mid=(l+r)>>1;
build(l,mid-1,mid);
build(mid+1,r,mid);
f[mid]=last;
update(mid);
if (mid<last)
ch[last][0]=mid;
else
ch[last][1]=mid;
}
int find(int k,int rank)
{
pushdown(k);
int l=ch[k][0],r=ch[k][1];
if(size[l]+1==rank) return k;
else if(size[l]>=rank) return find(l,rank);
else return find(r,rank-size[l]-1);
}
void Add(int l,int r,int v)
{
int x=find(root,l),y=find(root,r+2);
splay(root,x);
splay(ch[x][1],y);
int z=ch[y][0];
add[z]+=v,mx[z]+=v,num[z]+=v;
}
void reverse(int l,int r)
{
int x=find(root,l),y=find(root,r+2);
splay(root,x);
splay(ch[x][1],y);
rev[ch[y][0]]^=1;
}
void query(int l,int r)
{
int x=find(root,l),y=find(root,r+2);
splay(root,x),splay(ch[x][1],y);
printf("%d\n",mx[ch[y][0]]);
}
int main()
{
mx[0]=-0x7ffffff;
read(m),read(n);
build(1,m+2,0);
root=(m+3)>>1;
for(int i=1;i<=n;i++)
{
int flag,l,r,val;
read(flag),read(l),read(r);
if(flag==1) read(val),Add(l,r,val);
else if(flag==2) reverse(l,r);
else query(l,r);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号