BZOJ2726【SDOI2012】任务安排(斜率优化Dp+二分查找)
zz:https://www.cnblogs.com/xiannvzuimei/p/9602127.html
由题目条件显然可以得到状态 f[i][j] 表示以 i 为结尾且 i 后作为断点,共做了 j 次分组的最小代价。
因此转移变得很显然:f[i][j]=min{f[k][j-1]+(s×j+sumT[i])×(sumC[i]-sumC[k])} (0≤k<i)
sumT[i]表示时间的前缀和,sumC[i]表示代价的前缀和
但是绝望的是显然时间复杂度是O(n³),2D/1D的动态规划显然无法解决一题(但是如果能使用斜率优化也可以优化为O(n²)的程度,但显然毫无卵用QAQ)
所以我们来优化状态,无法避免对 i 的枚举,所以优化 j 成了必然,由于在转移中出现了s×j这恐怖的一项,导致不得不去枚举 j 的数值,但是我们将s×j提出,不难发现对于每组机器的开机时间 s 对最终答案造成的影响是 s×(sumC[n]-sum[k]),所以我们对当前的状态提前加上这个值,就可以很巧妙的避免了对 j 的枚举。
所以新的状态油然而生 f[i] 表示前 i 个任务当前断点在 i 后的最小代价。
转移也很是自然:f[i]=min{f[j]+(s+sumT[i])×(sumC[i]-sumC[j])}+s×(sumC[n]-sumC[i])
此时这个1D/1D的动态规划在此时已经在状态的维度上达到了最优,所以一堆大佬已经开始了斜率优化切题过程,但是作为蒟蒻的我们还是先来研究一下斜率优化的本质QWQ。
……
不妨先来降低一波难度吧假设对于所有时间 T 都是正的,我们该如何解决这道题呢?
显然这无数转移之中我们早可以隐约发现其中有无数不必要的枚举,所以我们可以假设 j1<j2<i 时,对于当前的 i 来说 j2 比 j1 更优,不难得到一下的式子:
f[j1]+(s+sumT[i])×(sumC[i]-sumC[j1])≥f[j2]+(s+sumT[i])×(sumC[i]-sumC[j2])
由于有关 i 的变量在此时对于当前状态来说相当于常量,所以我们应该将与 i 有关的式子移到一边,可得:
f[j2]-f[j1]-s×(sumC[j2]-sumC[j1])≤sumT[i]×(sumC[j2]-sumC[j1])
同除以(sumC[j2]-sumC[j1])得:
f[j2]-f[j1]-s×(sumC[j2]-sumC[j1])/(sumC[j2]-sumC[j1])≤sumT[i]
所以当满足以上的关系式的时候,对于状态 i 来说 j1 已经无用,j2 仍是有用的。
所以我们不妨设G(j1,j2)=f[j2]-f[j1]-s×(sumC[j2]-sumC[j1])/(sumC[j2]-sumC[j1]),
若出现 j1,j2,j3 时,当G(j1,j2)≥G(j2,j3)这种情况发生时,无论sumT[i]取何值,j2都不可能为最优。(这一步的讨论十分关键)
由此我们需要维护一个严格单调递增的队列即可对于当前的状态 i O(1)求出它的最有转移,这就是我们俗称的斜率优化。
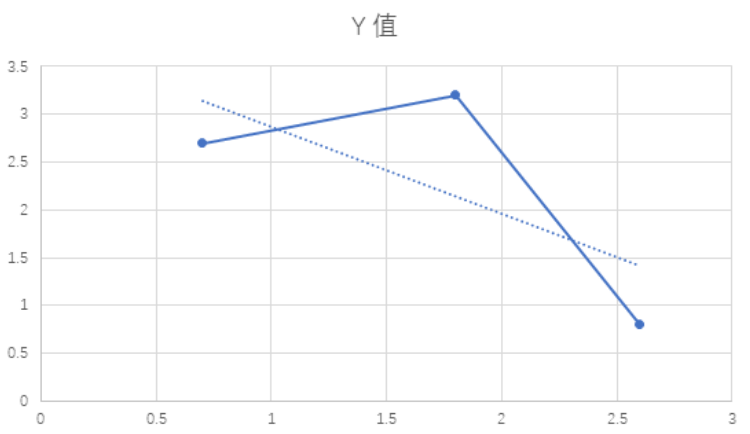
如果在坐标系中分析,则更为清晰对于虚线而言,实线连接的三个点中中间的点永远不可能成为最用,随即这便是斜率优化名称的由来,因为它像极了斜率的式子,我们只需要维护一个凹壳就可以了!!!QWQ
……
分析完水题我们再来看一看原题吧,如果 T 又负数,相当于 sumT[i] 不是单调的,我们仍需要维护凹壳,因为它满足我们上方证明的最优性,所以我们在查找上需要花点心思,仔细一想这也非常简单,只需要二分出适合于当前斜率 sumT[i] 的区间,也就是寻找 G(j2,j3)>=sumT[i] 且 G(j1,j2)<=sumT[i],则此时 j2 为当前的最有转移QAQ,代码实现也没有什么难度嘻嘻!!!
所以善良的我会告诉你们代码如下:
#include<cstdio>
#include<algorithm>
#define rep(i,l,r) for (int i=l; i<=r; i++)
typedef long long ll;
using namespace std;
const int N=1000010;
ll T[N],F[N],f[N];
int n,s,S,st,ed,q[N];
ll Y(int j){ return f[j]-F[n]*T[j]+F[j]*T[j]-F[j]*S; }
void dp(){
st=ed=0;
rep(i,1,n){
int l=0,r=ed-1,ans=ed;
while (l<=r){
ll mid=(l+r)>>1;
if (1ll*(F[q[mid+1]]-F[q[mid]])*T[i]<=Y(q[mid+1])-Y(q[mid])) ans=mid,r=mid-1; else l=mid+1;
}
int j=q[ans]; f[i]=f[j]+(F[n]-F[j])*(T[i]-T[j]+S);
while (st<ed && 1ll*(Y(q[ed])-Y(q[ed-1]))*(F[i]-F[q[ed]])>=(Y(i)-Y(q[ed]))*(F[q[ed]]-F[q[ed-1]])) ed--;
q[++ed]=i;
}
}
int main(){
scanf("%d%d",&n,&S);
rep(i,1,n) scanf("%lld%lld",&T[i],&F[i]),T[i]+=T[i-1],F[i]+=F[i-1];
dp(); printf("%lld\n",f[n]);
return 0;
}



