【bzoj4668】冷战
zz:https://www.cnblogs.com/GXZlegend/p/7423753.html
1946 年 3 月 5 日,英国前首相温斯顿·丘吉尔在美国富尔顿发表“铁幕演说”,正式拉开了冷战序幕。
美国和苏联同为世界上的“超级大国”,为了争夺世界霸权,两国及其盟国展开了数十年的斗争。在这段时期,虽然分歧和冲突严重,但双方都尽力避免世界范围的大规模战争(第三次世界大战)爆发,其对抗通常通过局部代理战争、科技和军备竞赛、太空竞争、外交竞争等“冷”方式进行,即“相互遏制,不动武力”,因此称之为“冷战”。
Reddington 是美国的海军上将。由于战争局势十分紧张,因此他需要时刻关注着苏联的各个活动,避免使自己的国家陷入困境。苏联在全球拥有 N 个军工厂,但由于规划不当,一开始这些军工厂之间是不存在铁路的,为了使武器制造更快,苏联决定修建若干条道路使得某些军工厂联通。Reddington 得到了苏联的修建日程表,并且他需要时刻关注着某两个军工厂是否联通,以及最早在修建哪条道路时会联通。具体而言,现在总共有M 个操作,操作分为两类:
• 0 u v,这次操作苏联会修建一条连接 u 号军工厂及 v 号军工厂的铁路,注意铁路都是双向的;
• 1 u v, Reddington 需要知道 u 号军工厂及 v 号军工厂最早在加入第几条条铁路后会联通,假如到这次操作都没有联通,则输出 0;作为美国最强科学家, Reddington 需要你帮忙设计一个程序,能满足他的要求。
输入
第一行两个整数 N, M。
接下来 M 行,每行为 0 u v 或 1 u v 的形式。
数据是经过加密的,对于每次加边或询问,真正的 u, v 都等于读入的
u, v 异或上上一次询问的答案。一开始这个值为 0。
1 ≤ N, M ≤ 500000,解密后的 u, v 满足1 ≤ u, v ≤ N, u不等于v
输出
对于每次 1 操作,输出 u, v 最早在加入哪条边后会联通,若到这个操
作时还没联通,则输出 0。
样例输入
5 9
0 1 4
1 2 5
0 2 4
0 3 4
1 3 1
0 7 0
0 6 1
0 1 6
1 2 6
样例输出
0
3
5
题解
并查集按秩合并+朴素LCA
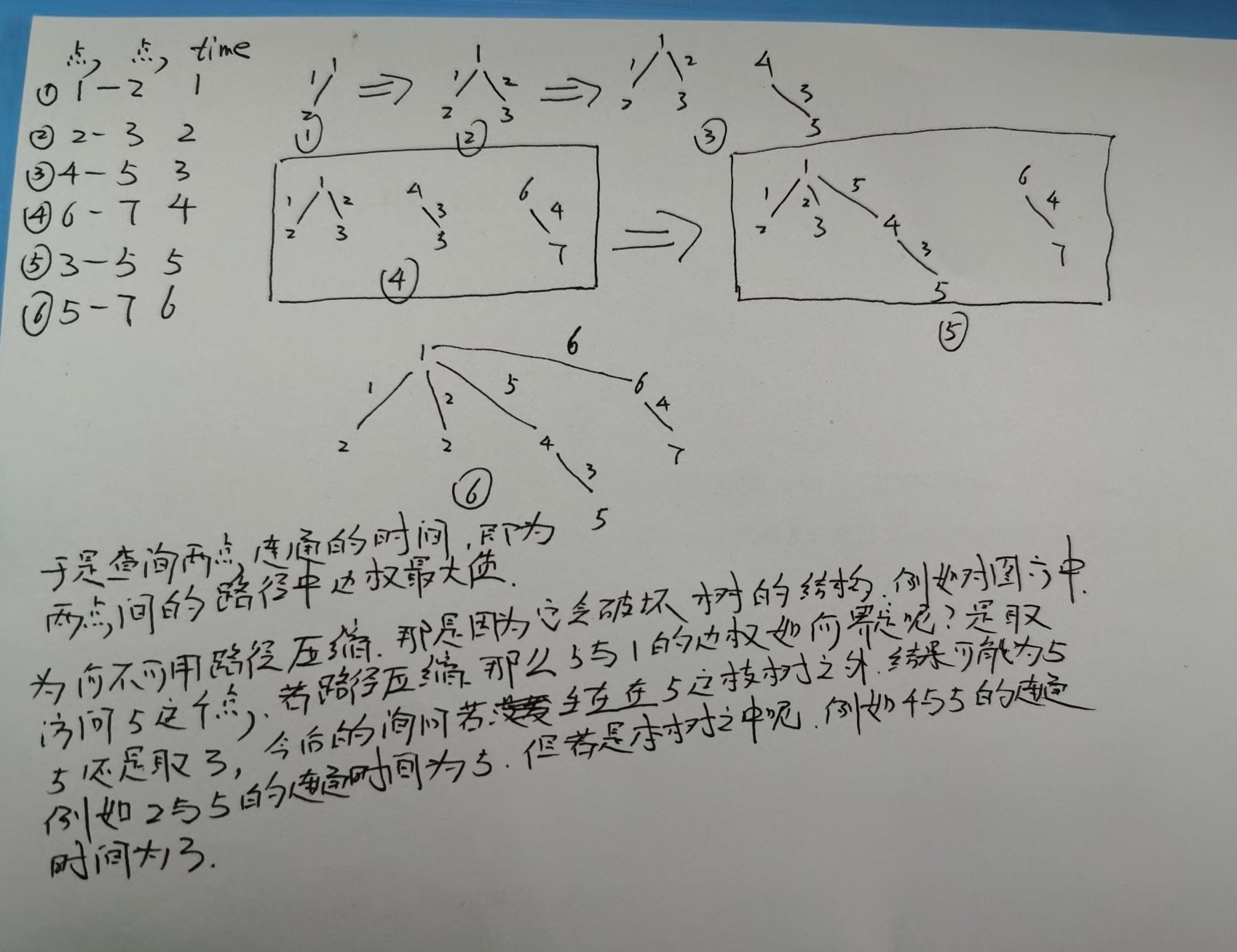
首先答案一定是在时间顺序的最小生成森林上,即如果两个点没有连通就把它们连上,最后得到的森林。
那么只需要维护连通性并支持快速查询即可。
考虑使用并查集的按秩合并,即按树高合并,这样树高只有logn,可以使用朴素LCA直接求解。
时间复杂度O(mlogn)
注意此题不能写路径压缩,因为那样会破坏树的形态!另按秩合并一般用在可撤销并查集操作上.
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 500010
using namespace std;
int fa[N] , v[N] , h[N] , cnt , tot;
int find(int x)
{
return fa[x] ? find(fa[x]) : x;
}
int deep(int x)
{
return fa[x] ? deep(fa[x]) + 1 : 0;
}
void add(int x , int y , int z)
{
x = find(x) , y = find(y);
if(x != y)
{
cnt ++ ;
if(h[x] < h[y]) //如果y所在的树更高,则将x所在的树合并到y上
fa[x] = y , v[x] = z; //x的父亲设为y,x加入树的时间点为z(这个x是参数x的根结点哟)
else
fa[y] = x , v[y] = z;
if(h[x] == h[y])
h[x] ++ ;
}
}
int query(int x , int y)
{
if(find(x) != find(y)) //没在一个块中
return 0;
int dx = deep(x) , dy = deep(y) , ans = 0;
while(dx > dy) //找出x到y的路径上的最大值
ans = max(ans , v[x]) , x = fa[x] , dx -- ;
while(dx < dy)
ans = max(ans , v[y]) , y = fa[y] , dy -- ;
while(x != y)
ans = max(ans , max(v[x] , v[y])) , x = fa[x] , y = fa[y];
return ans;
}
int main()
{
int m , opt , x , y , last = 0;
scanf("%*d%d" , &m);
while(m -- )
{
scanf("%d%d%d" , &opt , &x , &y) , x ^= last , y ^= last;
if(opt) //查询x,y是什么时候连通的
printf("%d\n" , last = query(x , y));
else //x,y在第tot的时候连在一起
add(x , y , ++tot);
}
return 0;
}
另一个写得有意思的代码:
#include<bits/stdc++.h> #define N 500005 using namespace std; int n,m,fa[N],lastans=0,siz[N],f[N],dep[N],tim=0; inline int read(){ int ans=0; char ch=getchar(); while(!isdigit(ch))ch=getchar(); while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar(); return ans; } inline void write(int x){ if(x>9)write(x/10); putchar((x%10)^48); } inline int find(int x){ if(x==fa[x])return x; int fx=find(fa[x]); dep[x]=dep[fa[x]]+1; return fx; } inline void merge(int x,int y) //按连通块的大小进行合并,小块并到大块上
{ int fx=find(x),fy=find(y); if(fx==fy)return; if(siz[fx]<siz[fy])fx^=fy,fy^=fx,fx^=fy; siz[fx]+=siz[fy],f[fy]=tim,fa[fy]=fx; } inline int query(int x,int y){ int fx=find(x),fy=find(y); if(fx^fy)return 0; int ans=0; while(x^y) //这个求路径上的最大值写得很清爽啊
{ if(dep[x]<dep[y])x^=y,y^=x,x^=y; ans=max(ans,f[x]); x=fa[x]; } return ans; } int main(){ n=read(),m=read(); for(int i=1;i<=n;++i)fa[i]=i,siz[i]=1; while(m--){ int op=read(),x=lastans^read(),y=lastans^read(); if(!op)++tim,merge(x,y); else write((lastans=query(x,y))),puts(""); } return 0; } ———————————————— 版权声明:本文为CSDN博主「SC.ldxcaicai」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/dreaming__ldx/article/details/81915488





