算法刷题-尼科彻斯定理-JAVA

0x00 引言

为获取一个良好的算法思维，以及不再成为一个脚本小子，争取每天一道算法题，培养自己的逻辑思维，温顾各类型语言语法知识。

题解只写自己理解的解法，其他解法不再增加。题目与解析均在代码里面。

0x01 难度等级

简单

0x02 代码

package 简单;

import java.util.Scanner;

/*
*
*
*
描述
验证尼科彻斯定理，即：任何一个整数m的立方都可以写成m个连续奇数之和。

例如：

1^3=1

2^3=3+5

3^3=7+9+11

4^3=13+15+17+19

输入一个正整数m（m≤100），将m的立方写成m个连续奇数之和的形式输出。
数据范围：
1
≤
�
≤
100

1≤m≤100

输入描述：
输入一个int整数

输出描述：
输出分解后的string
*
示例1
输入：
6
*
输出：
m^3=m^a1+m*(m-1)  2与d(公差2约掉了)
6^3=31+33+35+37+39+41
*
* */
public class 尼科斯彻定理 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        double a1 = 0;
        double x = Math.pow(m, 2);//m^3=m^a1+m*(m-1)
        a1 = x - m + 1;//36-6+1   a1=m^2-m+1
        int b = 0;
        int[] arr = new int[m];
//        System.out.println(a1);
        for (int i = 0; i < m; i++) {
            b = (int) a1;//31
            b += 2 * i;//31
            arr[i] = b;//31
            if (i == m - 1) {//5
                System.out.print(arr[i]);//41就不打印“+号”
            } else {
                System.out.print(arr[i] + "+");
            }

        }
    }
}

 

0x03 算法思想

考查公差d为2的等差数列的通项求和公式：m设为项数，先计算处a1，再计算出每一项，一共只有m项。

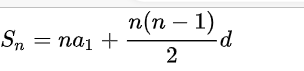
m^3=m^a1+m*(m-1)

0x04 运行结果