SDF矩形(附圆角)公式推导
SDF矩形(附圆角)公式推导
矩形
一般情况下,我们会使用(top_left, top_bottom), (width, height)来定义一个矩形,但是对于SDF而言,使用(centerX, centerY), (HalfSizeX, HalfSizeY)会更方便一些。
假设一个矩形,我们先定义原点在(0, 0),那图像如下:
记住要计算的内容:点与形状最近边缘之间的距离。
那么会出现两种情况,当要计算矩形内的点与矩形最近边缘的距离时,我们可以看下下图的表示:
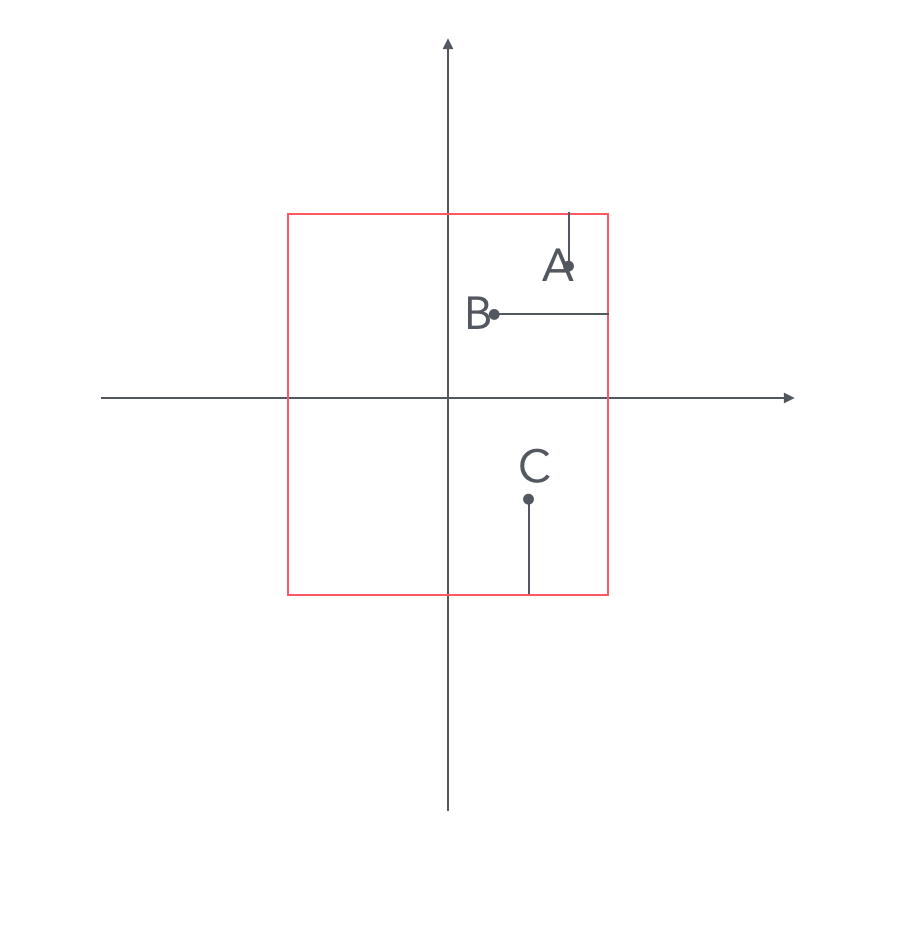
找到最近的边缘,然后做垂线就可以计算出SDF值,A,B,C点皆是如此。
但是对于形状外的点,情况就有些不同:
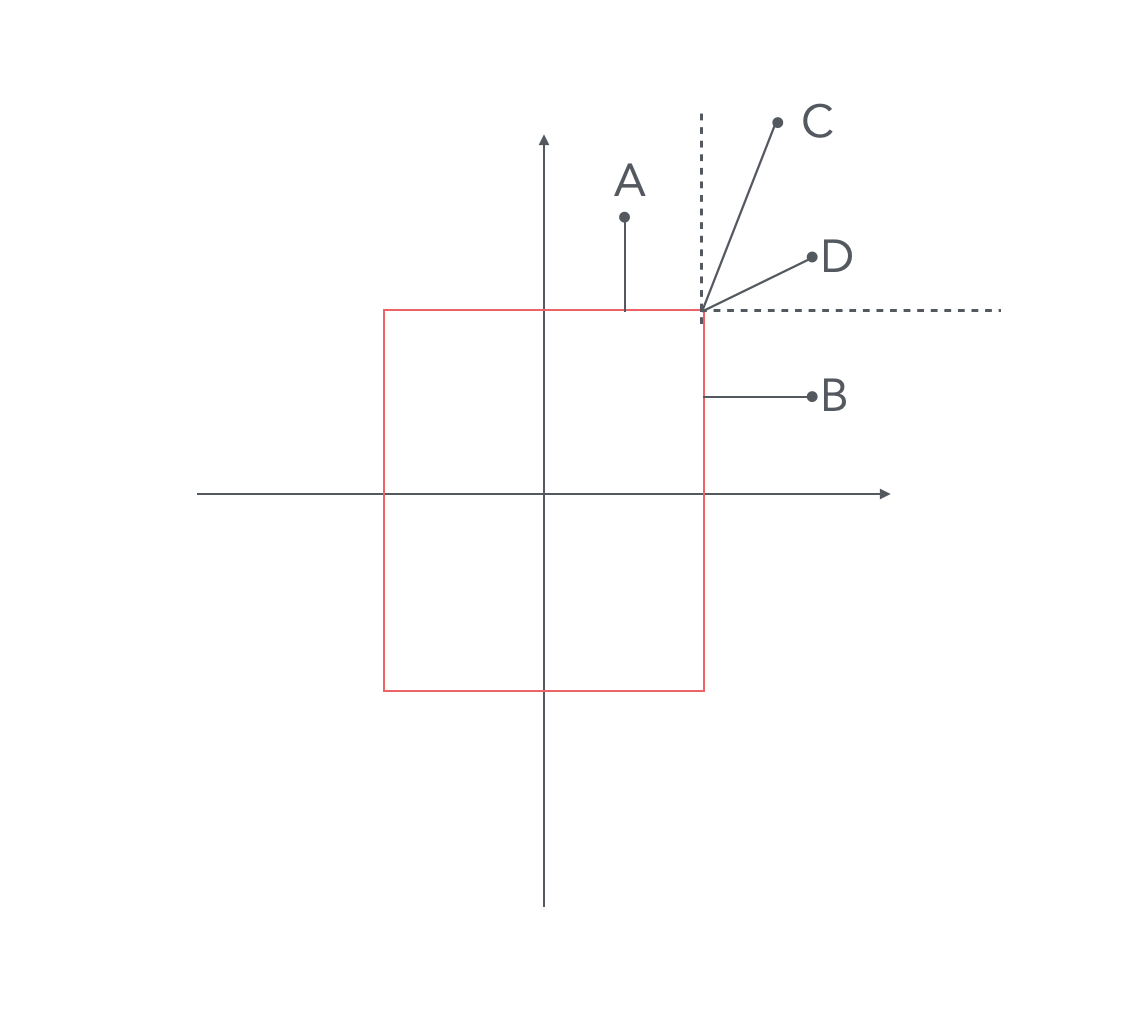
对于AB点来说,情况是一致的,找到最近的边缘,然后就可以得到距离了。
但是我们发现,对于C,D点,矩形内点与矩形最近边缘的距离其实是到角点E的距离。所以当计算矩形SDF时候,要考虑这种特殊情况,在第一象限的时候,代码如下:
float sdf_rect(vec2 point, vec2 half_size) {
point = abs(point);
// 计算每个点到两个边的距离
float x_dist = point.x - half_size.x;
float y_dist = point.y - half_size.y;
// 如果一正一负,或者全是负数
// 则可以直接取max(x_dist, y_dist)作为对应点的SDF值
// distance to corner
float c_dist = length(point - half_size); // 求到corner的距离
// 如果都为正数,说明是C、D点的情况,则要返回到corner的距离
float res = x_dist > 0.0 && y_dist > 0.0 ?
c_dist :
max(x_dist, y_dist);
return res;
}
那对于其他象限呢,要知道,一个矩形是对称的,所以要求的其他象限的点的SDF值,可以都映射到第一象限去求:
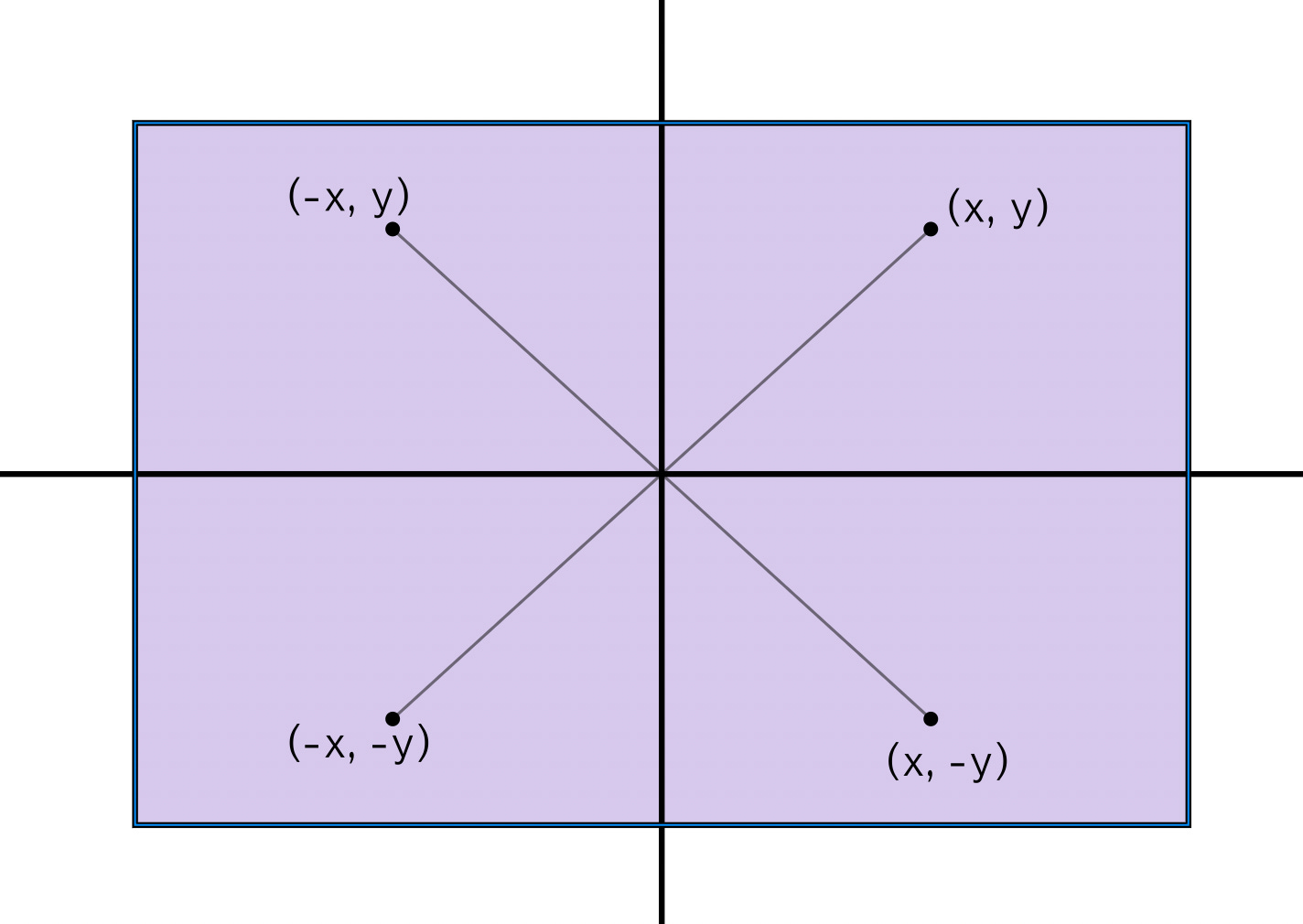
最终的代码是这样的:
float sdf_rect(vec2 point, vec2 half_size) {
point = abs(point);
// 计算每个点到两个边的距离
float x_dist = point.x - half_size.x;
float y_dist = point.y - half_size.y;
// 如果一正一负,或者全是负数
// 则可以直接取max(x_dist, y_dist)作为对应点的SDF值
// distance to corner
float c_dist = length(point - half_size); // 求一下到corner的距离
// 如果都为正数,说明是C、D点的情况,则要返回到corner的距离
float res = x_dist > 0.0 && y_dist > 0.0 ?
c_dist :
max(x_dist, y_dist);
return res;
}

进一步探讨
圆角矩形
现在的设备设计都开始讲究一个圆角矩形了,比如苹果的各种设备,我们也希望得到的矩形是一个圆角。

答案很简单,就是将最终的SDF值减去一个r,对的,就是这么简单。
我们知道,处在矩形边缘上的点的SDF值是0,如果把所有相同值的SDF化成一条线,则可以得到一个类似这样的等高线图。

其实问题的关键(问题的关键就是关键的问题?🐶)在角点处,角点处相同的SDF值连成的等高线是一个圆,所以SDF值做减法的时候,形状会变成圆角,这里的r一般情况下可以根据矩形的边长进行线性的设置大小。
提供一种比较好理解的方式就是因为SDF是一个函数,输入的是一个平面上每一个点的坐标,输出是每个点到0平面的距离。当减去一个r的时候,要再得到0平面,则原先的SDF值需要扩大到原来的r位置。
如果是做加法呢,矩形会变得比之前小,但是不是圆角。
镂空矩形

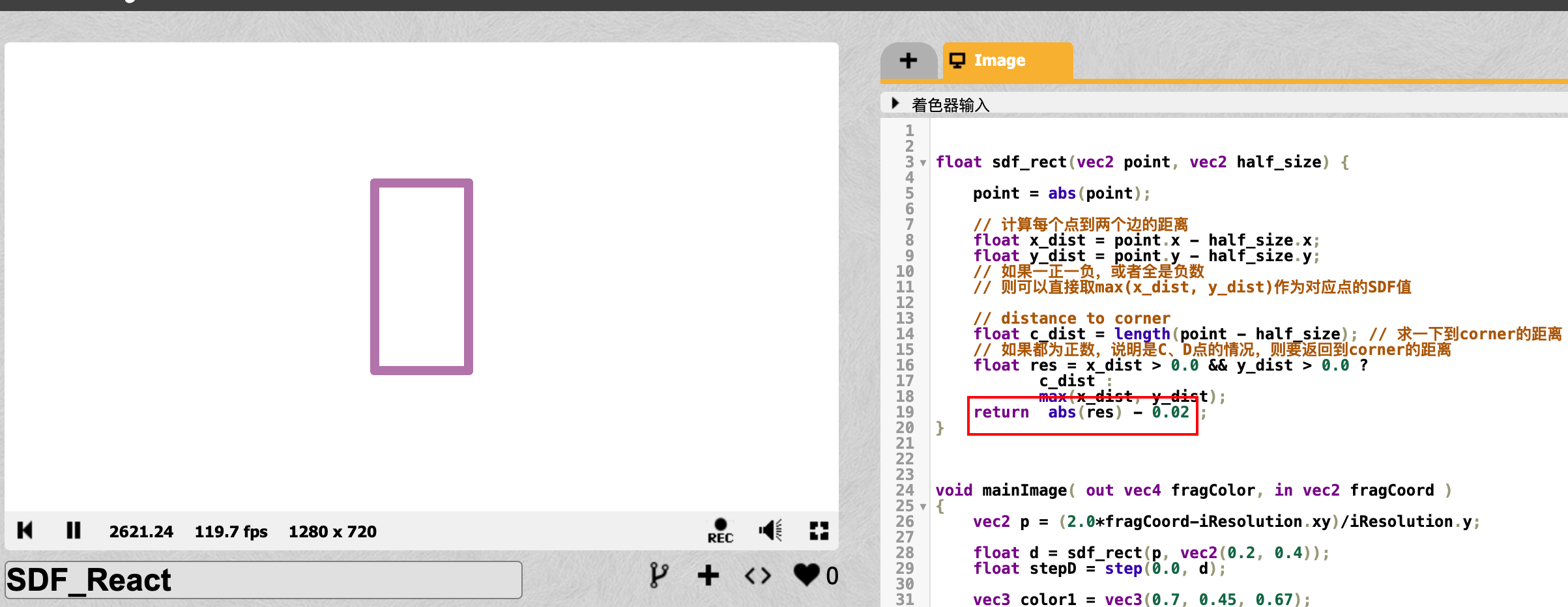
具体的解释和上面圆角矩形的设置是一样的,核心是找到+r 和 -r所在的那个等高线,然后分析一下值的变化。
相关代码: https://www.shadertoy.com/view/MXVXDc
refer
本文来自博客园,作者:CuriosityWang,转载请注明原文链接:https://www.cnblogs.com/curiositywang/p/18294750


