numpy常用函数记录

np.square()

函数返回一个新数组，该数组的元素值为源数组元素的平方。 源阵列保持不变。

示例:

import numpy as np

a = np.array([[1, 2, 3],
             [4, 5, 6]])
b = np.square(a)
print(a)
print(b)

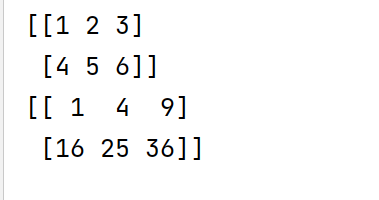
np.linalg.norm()

linalg = linear(线性) + algebra(代数)， norm表示范数

x_norm = np.linalg.norm(x, ord=None, axis=None, keepdims=False)

• x代表矩阵,可以是一维
• axis=0,按列向量处理,求多个列向量的范数;axis=1,按行向量处理,求多个行向量的范数
• ord矩阵的范数

ord常用参数 当x是向量时

参数	说明	计算方法
默认	二范数	\(\sqrt{x_1^2 + x_2^2+ ...+x_n^2}\)
ord=2	同上	同上
ord=1	一范数	$
ord="fro"	Frobenius范数:其值为对所有元素的绝对值的平方求和后开平方。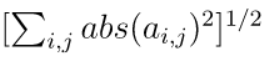

ord常用参数 当x是矩阵时

参数	计算方法
ord=1	列和的最大值
ord=2	求特征值，然后求最大特征值得算术平方根

注意,当x是矩阵时,参数axis才有意义

示例:

import numpy as np

a = np.array([[1, 2, 3],
             [4, 5, 6]])
x1 = np.linalg.norm(a, ord=2)
x2 = np.linalg.norm(a, ord=1)
x3 = np.linalg.norm(a, ord=2, axis=1)
print(x1)
print(x2)
print(x3)

np.martix()

自带广播功能

import numpy as np

M = np.array([[1, 2, 3],
                [4, 5, 6]])

test = np.array([[1, 2, 3],
                [1, 2, 2]])

train = np.array([[1, 1, 1],
                  [1, 1, 1],
                    [1, 1, 1]])

te = np.square(test).sum(axis=1)
tr = np.square(train).sum(axis=1)
te = te.reshape(te.shape[0], -1)
print("te:", te)
print("tr:", tr)

dists = M + np.matrix(tr) + np.matrix(te)
print(dists)

各变量的变化情况:

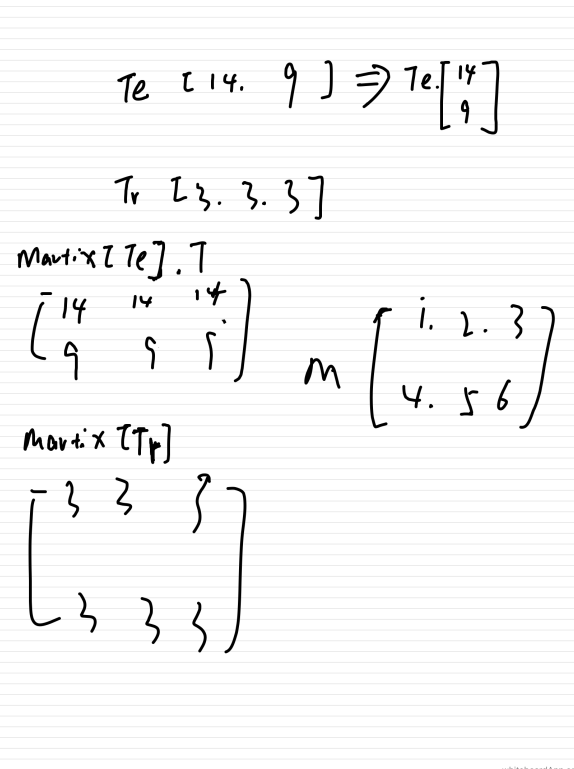
np.array_split(x, n)

将矩阵x切割为七部分

import numpy as np

x = np.arange(25)
y = np.array_split(x, 7)

print(type(y))
print(y)

返回了一个列表

np.concatenate(x, axis=?)

import numpy as np

x = np.arange(25)
print(x)

y = np.array_split(x, 7)
print(y)

print(np.concatenate(y))

axis = 0 列方向对齐

axis = 1 行方向对齐

np.square()

沿着水平方向将数组堆叠起来。

import numpy as np


arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
res = np.hstack((arr1, arr2))

print(res)


arr1 = np.array([[1, 2], [3, 4], [5, 6]])
arr2 = np.array([[7, 8], [9, 0], [0, 1]])
res = np.hstack((arr1, arr2))

print(res)

np.eye()

import numpy as np

labels = np.array([[1, 3],[2, 3],[0, 2],[1, 3]])
print(labels.shape)
print(labels, "\n\n**********\n")

x = np.eye(5)[labels]
print(x)
print(x.shape)

大概这样理解,先生成一个shape为(4,2,5)的矩阵,意思就是4个2*5的矩阵.然后对某些地方的值赋1,什么地方那?也就是labels提供的位置

np.where

详见：https://www.cnblogs.com/massquantity/p/8908859.html