全排列与全组合

全排列

#include <bits/stdc++.h>
using namespace std;

int sum = 0;

int a[5] = {1,2,3,4,5};
int n = 5;

// p q 意义是对数组全排列的位置进行界定
void perm(int p, int q)
{

    //核心代码
    if(p == q)
    {
        for(int i = 0; i < n; i++)
            cout << a[i];
        cout << endl;
        sum++;
    }
    for(int i = p; i <= q; i++)
    {
        swap(a[p], a[i]);
        perm(p+1,q);
        swap(a[p], a[i]);
    }
}


int main()
{
    perm(0,4);
    return 0;
}

全组合

利用位图:假设原有元素 n 个，则最终组合结果是 2n−1 个。我们可以用位操作方法：假设元素原本有：a,b,c 三个，则 1 表示取该元素，0 表示不取。故取a则是001，取ab则是011。所以一共三位，每个位上有两个选择 0 和 1。而000没有意义，所以是2n−1个结果。

这些结果的位图值都是 1,2…2^n-1。所以从值 1 到值 2n−1 依次输出结果：

001,010,011,100,101,110,111 。对应输出组合结果为：a,b,ab,c,ac,bc,abc。

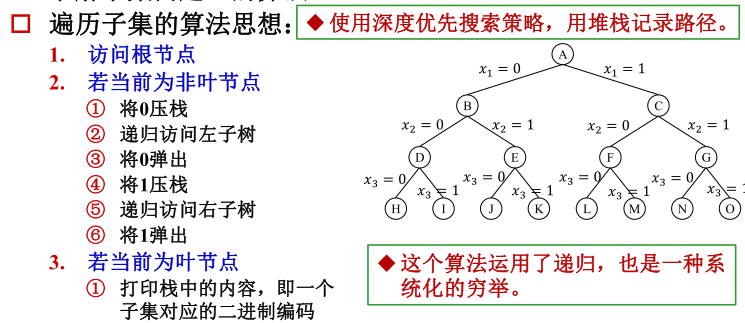
利用这棵状态空间树.

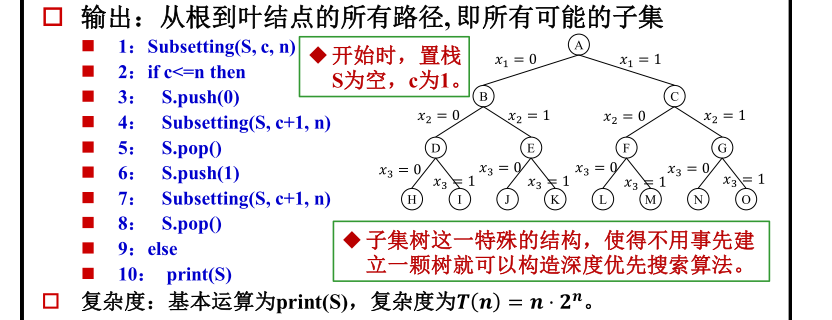
我们求某个集合的子集.

// 全组合实现
// 关键字 栈 递归

#include <bits/stdc++.h>

using namespace std;

vector <int> s;
int A[5] = {2,6,8,7,9};


void print(int n)
{
    // 利用子集数组,实现A的子集求解
    for(int i = 0; i < n; i++)
    {
         if(s[i] == 1)
        {
            cout << A[i];
        }
    }

    cout << endl;
}

void subsetting(int c, int n)
{
    if(c <= n)
    {
        s.push_back(0);
        subsetting(c+1, n);
        s.pop_back();
        s.push_back(1);
        subsetting(c+1, n);
        s.pop_back();
    }
    else
        print(n);
}


int main()
{
    subsetting(1,5);

    return 0;
}