蚁群算法
蚁群算法
引言
在自然界中各种生物群体显现出来的智能近几十年来得到了学者们的广泛关注,学者们通过对简单生物体的群体行为进行模拟,进而提出了群智能算法。其中,模拟蚁群觅食过程的蚁群优化算法(Ant Colony Optimization, ACO)和模拟鸟群运动方式的粒子群算法是两种最主要的群体智能算法。本文介绍蚁群优化算法(简称蚁群算法)。
蚁群算法是一种源于大自然生物世界的新的仿生进化算法,是由意大利学者M.Dorigo等人于20世纪90年代初期通过模拟自然界中蚂蚁集体寻经行为而提出的一种基于种群的启发式随机搜索算法。蚂蚁有能力在其走过的路径上释放一种特殊的分泌物——信息素,随着时间的推移该物质会逐渐挥发,后来的蚂蚁选择该路径的概率与当时这条路经上的信息素强度成正比。当一条路径上通过的蚂蚁越来越多时,其留下的信息素越来越多,后来蚂蚁选择该路径的概率也就越高,从而更增加了该路径上的信息素强度。而强度大的信息素会吸引更多蚂蚁,从而形成一种正反馈机制。通过这种正反馈机制,蚂蚁最终可以发现最短路径。
蚁群算法理论
蚁群算法是对自然界蚂蚁的寻径方式进行模拟而得出的一种仿生算法。蚂蚁在运动过程中,能够在它所在的路径上留下信息素进行信息传递,而且蚂蚁在运动过程中能够感知这种物质,并以此来指导自己的运动方向。因此,由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象:某一路径上走过的蚂蚁越多,则后来者选择该路径的概率就越大。
真实蚁群的觅食过程
为了说明蚁群算法的原理,先简要介绍一下蚂蚁搜寻食物的具体过程。在自然界中,蚁群在寻找食物时,它们总能找到一条从食物到巢穴之间的最优路径。这是因为蚂蚁在寻找路径时会在路径上释放出一种特殊的信息素。蚁群算法的信息素交互主要是通过信息素来完成的。蚂蚁在运动过程中,能够感知到这种物质的存在和强度。初始阶段,环境中并没有信息素的遗留,蚂蚁寻找食物完全是随机选择路径,随后寻找该食物源的过程中就会受到先前蚂蚁所残留的信息素的影响,其表现为蚂蚁在选择路径时趋向于选择信息素浓度高的路径。同时,信息素是一种挥发性化学物质,会随着时间的推移而慢慢地消逝。如果每只蚂蚁在单位距离留下的信息素相同,那对较短路径上残留的信息素浓度就相对较高,这被后来的蚂蚁选择的概率就大,从而导致这条路径上走的蚂蚁就越多。而经过的蚂蚁越多,该路径上残留的信息素就将更多,这样使得整个蚂蚁的集体欣慰构成了信息素的正反馈过程,最终整个蚁群会找出最优路径。
人工蚁群的优化过程
基于以上真实蚁群寻找食物时的最优路径选择问题,可以构造人工蚁群解决最优化问题,如旅行商问题(TSP)。人工蚁群中把具体简单功能的工作单元看作蚂蚁。二者的相似之处在于都是优化选择信息素浓度大的路径。较短路径的信息素浓度高,所以能够最终被所有蚂蚁选择,也就是最终的优化结果。两者的区别在于人工蚁群有一定的记忆能力,能够记忆已经访问过的节点。同时,人工蚁群再选择下一条路径的时候是按照一定算法规律有意识地寻找最优路径,而不是盲目的。例如在TSP中,可以预先知道当前城市到下一个目的地的距离。
在TSP的人工蚁群算法中,假设m只蚂蚁在图的相邻节点间移动,从而协作异步地得到问题的解。每只蚂蚁的一步转移概率由图中的每条边上的两类参数决定:一是信息素值,也称信息素痕迹;二是可见度,即经验值。
信息素的更新方式有两种:
- 挥发。也就是所有路径上的信息素以一定的比率减少,模拟自然蚁群的运动是通过一个随时间挥发的过程。
- 增强。给评价值“好”(有蚂蚁走过)的边增加信息素。
蚂蚁向下一个目标的运动是通过一个随机原则来实现的,也就是运用当前节点存储的信息,计算出下一步可达节点的概率,并按此概率实现一步移动。如此往复,越来越接近最优解。
蚂蚁在寻径过程中,或在找到一个解之后,会评估该解或解的一部分的优化程度,并把评价信息保存在相关连接的信息素中。
真实蚂蚁与人工蚂蚁的异同
蚁群算法是一种基于群体的、用于求解复杂优化问题的通用搜索技术。与真实蚂蚁通过外信息的留存、跟随行为进行间接通信相似,蚁群算法中一群见到那的人工蚂蚁通过信息素进行间接通信,并利用该信息和与问题相关的启发式信息逐步构造问题的解。
人工蚂蚁具有双重特性:
- 它们是真实蚂蚁的抽象,具有真实蚂蚁的特性
- 它们还有一些真实蚂蚁没有的特性,这些新的特性使得人工蚂蚁在解决实际优化问题时,具有更好地搜索最优解的能力。
人工蚂蚁与真实蚂蚁的相同点为:
- 都是一群相互协作的个体
- 都使用信息素的迹和蒸发机制
- 搜索最短路径与局部移动
- 随机状态转移策略
人工蚂蚁和真实蚂蚁的不同点:
- 人工蚂蚁生活在离散的时间上,从一种离散状态到另一种离散状态
- 人工蚂蚁具有内部状态,即人工蚂蚁具有一定的记忆能力,能记住自己走过的地方
- 人工蚂蚁释放信息素的数量是其生成解的质量的函数
- 人工蚂蚁更新信息素的时机依赖于特定的问题。例如,大多数人工蚂蚁仅仅在其找到一个解之后才更新路径上的信息素
蚁群算法的特点
蚁群算法是通过对生物特征的模拟得到的一种优化算法,它本身具有很多优点:
- 蚁群算法是一种本质上的并行算法。每只蚂蚁搜索的过程彼此独立,仅通过信息素进行通信。所以蚁群算法可以看作一种分布式的多智能体系统,它在问题空间的多点同时开始独立的解搜索。不仅增加了算法的可靠性,也使得算法具有较强的全局搜索能力
- 蚁群算法是一种自组织的算法。所谓自组织,就是组织力或组织指令来自系统的内部,以区别于其他组织。如果系统在获得空间、时间或者功能结构的过程中,没有外界的特定干预,就可以说系统是自组织的。简单地说,自组织是系统从无序到有序的变化过程
- 蚁群算法具有较强的鲁棒性。相对于其他算法,蚁群算法对初始路线的要求不高,即蚁群算法的求解结果不依赖于初始路线的选择,而且在搜索过程中不需要进行人工的调整。此外,蚁群算法的参数较少,设置简单,因而该算法易于应用到组合优化问题的求解
- 蚁群算法是一种正反馈算法。从真实蚂蚁的觅食过程中不难看出,蚂蚁能够最终找到最优路径,直接依赖于其在路径上信息素的堆积,而信息素的堆积是一个正反馈的过程。正反馈是蚁群算法的重要特征,它使得算法进行过程得以进行
基本蚁群算法及流程
这里以旅行商问题(TSP)为例介绍基本蚁群算法及其流程。基本蚁群算法可以表述如下:
在算法的初始时刻,将m只蚂蚁随机地放到n个城市中,同时,将每只蚂蚁的禁忌表tabu的第一个元素设置为它当前所在的城市。此时各路径上的信息素量相等,设\(\tau_{ij} (0) = c\)(c为一个较小的常数),接下来,每只蚂蚁根据路径上残留的信息素量和启发式信息(两个城市的距离)独立地选择下一个城市,在时刻t,蚂蚁k从城市i转移到城市j的概率为\(p_{ij}^k (t)\)为
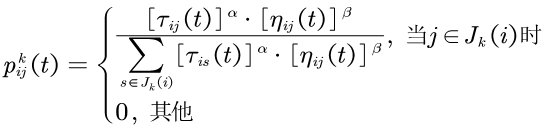
式中,\(J_k(i)=\{ 1, 2, ..., n \} - tabu_k\)表示蚂蚁k下一步允许选择的城市集合。禁忌表\(tabu_k\)记录了蚂蚁k当前走过的城市。当所有n个城市都加入到禁忌表\(tabu_k\)中时,蚂蚁k便完成了一次周游,此时蚂蚁k所走过的路径便是TSP的一个可行解。
\(\eta_{ij}\)是通常取城市i与城市j之间距离的倒数。\(\alpha\) 与 \(\beta\)分别表示信息素和期望启发式因子的相对重要程度。当所有蚂蚁完成一次周游后,各路径上的信息素根据下面的公式更新:
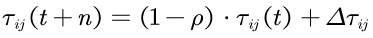
式中:\(\rho (0 < \rho < 1)\)表示路径上信息素的蒸发系数,\(1-\rho\)表示信息素的持久性系数;\(\varDelta\tau_{ij}\)表示本次迭代中边\(ij\)上信息素的增量,即
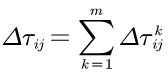
其中\(\varDelta \tau _{ij}^{k}\)表示第k只蚂蚁在本次迭代中留在边\(ij\)上的信息素量,如果蚂蚁k没有经过边\(ij\),则\(\varDelta \tau _{ij}^{k}\)的值为零。\(\varDelta \tau _{ij}^{k}\)可表示为:

式中,\(Q\)为正常数,\(L_k\)表示第k只蚂蚁在本次周游中所走过的路径的长度。
蚁群算法实际上是正反馈原理和启发式算法相结合的一种算法。在选择路径时,蚂蚁不仅利用了路径上的信息素,而且用到了城市间距离的倒数作为启发式因子。
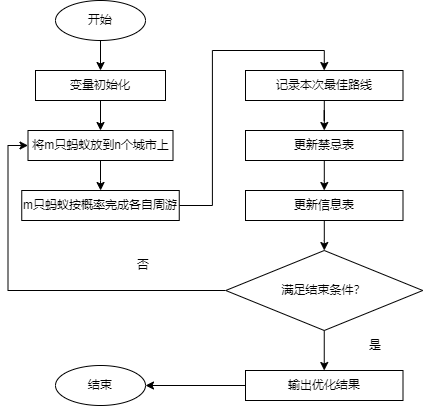
基本蚁群算法的具体实现步骤如下:
- 参数初始化。令时间\(t=0\)和循环次数\(N_c=0\),设置最大循环次数\(G\),将\(m\)只蚂蚁置于\(n\)个城市上,令有向图是国内每条边(i,j)的初始化信息量\(\tau_{ij} (t)=c\),其中\(c\)表示常数,且初始时刻\(\varDelta\tau_{ij}(0)=0\).
- 循环次数\(N_c=N_c+1\)
- 蚂蚁的禁忌表索引号\(k=1\)
- 蚂蚁数目\(k=k+1\)
- 蚂蚁个体根据状态转移概率公式计算的概率选择元素\(j\)并前进,\(j\in\left\{J_k\left(i\right)\right\}\)
- 修改禁忌表指针,即选择好之后将蚂蚁移动到新的元素,并把该元素移动到该蚂蚁个体的禁忌表中
- 若集合\(C\)中的元素未遍历完,即\(k < m\),则跳转到第4步;否则,执行到第8步
- 记录本次最佳路线
- 更新每条路径上的信息量
- 若满足结束条件,即如果循环次数\(N_c \ge G\),则循环结束并输出程序优化结果;否则清空禁忌表并跳转到第2步
蚁群算法的运算流程图如下:
关键参数说明
在蚁群算法中,不仅信息素和启发函数乘积以及蚂蚁之间的合作行为会严重影响到算法的收敛性,蚁群算法的参数也是影响其求解性能和效率的关键因素。信息素启发式因子\(\alpha\)、期望启发因子\(\beta\)、信息素蒸发系数\(\rho\)、信息素强度\(Q\)、蚂蚁数目\(m\)等都是非常重要的参数,其选取方法和选取原则直接影响到蚁群算法的全局收敛性和求解效率。
信息素启发式因子\(\alpha\)
信息素启发式因子\(\alpha\)代表信息量对是否选择当前路径的影响程度,即反映蚂蚁在运动过程中所积累的信息量在指导蚁群搜索中的相对重要程度。\(\alpha\)的大小反映了蚁群在路径搜索中随机性因素作用的强度,其值越大,蚂蚁在选择以前走过的路径的可能性越大,搜索的随机性就会减弱;而当启发式因子\(\alpha\)的值过小时,则易使蚁群的搜索过早陷于局部最优。一般为\([1, 4]\)时,蚁群算法的综合求解性能较好。
期望启发因子\(\beta\)
期望启发因子\(\beta\)表示在搜索时路径上的信息素在指导蚂蚁选择路径时的向导性,它的大小反应了蚁群在搜索最优路径的过程中的先验性和确定性因素的作用强度。期望启发因子\(\beta\)的值越大,蚂蚁在某个局部点上选择局部最短路径的可能性就越大,虽然这个时候算法的收敛速度得以加快,但蚁群搜索最优路径的随机性减弱,而此时搜索易于陷入局部最优解。根据经验,期望启发因子\(\beta\)取值范围一般在\([3, 5]\),此时蚁群算法的综合求解性能较好。
实际上,信息素启发式因子\(\alpha\)和期望启发因子\(\beta\)是一对关联性很强的参数:
蚁群算法的全局寻优性能,首先要求蚁群的搜索过程必须要有很强的随机性;而蚁群算法的快速收敛性能,又要求蚁群的搜索过程必须要有较高的确定性。因此,两者对蚁群算法性能的影响和作用是相互配合、密切相关的,算法要获得最优解,就必须在这二者之间选取一个平衡点,只有正确选定它们之间的搭配关系,才能避免在搜索过程中出现过早停滞或陷入局部最优解等情况的发生。
信息素蒸发系数\(\rho\)
蚁群算法中的人工蚂蚁是具有记忆功能的,随着时间的推移,以前留下的信息素将会逐渐消逝,蚁群算法与其他各种仿生进化算法一样,也存在着收敛速度慢、容易陷入局部最优解等缺陷,而信息素蒸发系数\(\rho\)大小的选择将直接影响到整个蚁群算法的收敛速度和全局搜索性能。在蚁群算法的抽象模型中,\(\rho\)表示信息素蒸发系数,\(1-\rho\)则表示信息素持久性系数。因此,\(\rho\)的取值范围应该是\([0,1]\)之间的一个数,表示信息素的蒸发程度,它实际上反映了蚂蚁群体中个体之间相互影响的强弱。\(\rho\)过小时,则表示以前搜索过的路径被再次选择的可能性过大,会影响到算法的随机性能和全局搜索能力;\(\rho\)过大时,说明路径上的信息素挥发的相对变多,虽然可以提高算法的随机搜索性能和全局搜索能力,但过多无用搜索操作势必会降低算法的收敛速度。
蚂蚁数目\(m\)
蚁群算法是一种随机搜索算法,与其他模拟进化算法一样,通过多个候选解组成的群体进化过程来寻求最优解,在该过程中不仅需要每个个体的自适应能力,更需要群体之间的相互协作能力。蚁群在搜索过程中之所以表现出复杂有序的行为,是因为个体之间的信息交流与相互协作起着重要的作用。
对于旅行商问题,单个蚂蚁在一次循环中所经过的路径,表现为问题可行解集中的一个解,\(m\)只蚂蚁在一次循环中所经过的路径,则表现为问题解集中的一个子集。显然,子集增大(即蚂蚁数量增多),可以提高蚁群算法的全局搜索能力以及算法的稳定性;但蚂蚁数目增大后,会使大量的曾被搜索过的解上的信息素的变化趋于平均,信息正反馈的作用不明显,虽然搜索的随机性得到了加强,但收敛速度减;反之,子集较小,特别是当要处理的问题规模比较大时,会使那些从来未被搜索到的解上的信息素减小到接近于0,搜索的随机性减弱,虽然收敛速度加快了,的那会使算法的全局性能降低,算法的稳定性差,容易出现过早停滞现象。\(m\)一般取\([10, 50]\).
信息素强度\(Q\)对算法性能的影响
在蚁群算法中,各个参数的作用实际上是紧密联系的,其中对算法性能起到主要作用的是信息启发式因子\(\alpha\)、期望启发式因子\(\beta\)和信息素挥发因子\(\rho\)这三个参数,总信息量\(Q\)对算法性能的影响有依赖于上述三个参数的选取,以及算法模型的选取。
在算法参数的选择上,对参数\(Q\)不必进行特别的考虑,可以任意选取。
最大进化代数\(G\)
最大进化代数\(G\)是表示蚁群算法运行结束条件的一个参数,表示蚁群算法运行到指定的进化代数之后就停止运行,并将当前群体中的最佳个体作为所求问题的最优解输出。一般\(G\)取\([100,500]\).
MATLAB仿真实例
旅行商问题(TSP)。假设有一个旅行商人要拜访柳州20个景点,他需要选择所要走的路径,路径的限制是每个景点只能拜访一次,而且最后要回到原来出发的景点。路径的选择要求是:所选路径的路径为所有路径中最小的。
柳州20个景点的坐标为
citys =
109.4177 24.3085
109.4443 24.3086
109.4394 24.3089
109.4226 24.3090
109.4471 24.3092
109.4277 24.3093
109.4347 24.3101
109.4168 24.3102
109.4470 24.3167
109.4175 24.3186
109.4469 24.3230
109.4197 24.3240
109.4467 24.3285
109.4218 24.3313
109.4465 24.3350
109.4205 24.3372
109.4462 24.3392
109.4209 24.3397
109.4413 24.3415
109.4356 24.3418
因为个人不喜欢猪大肠的程序,所以我把原来书上的代码拆分成结构比较清晰的多文件。
项目目录如下图所示:
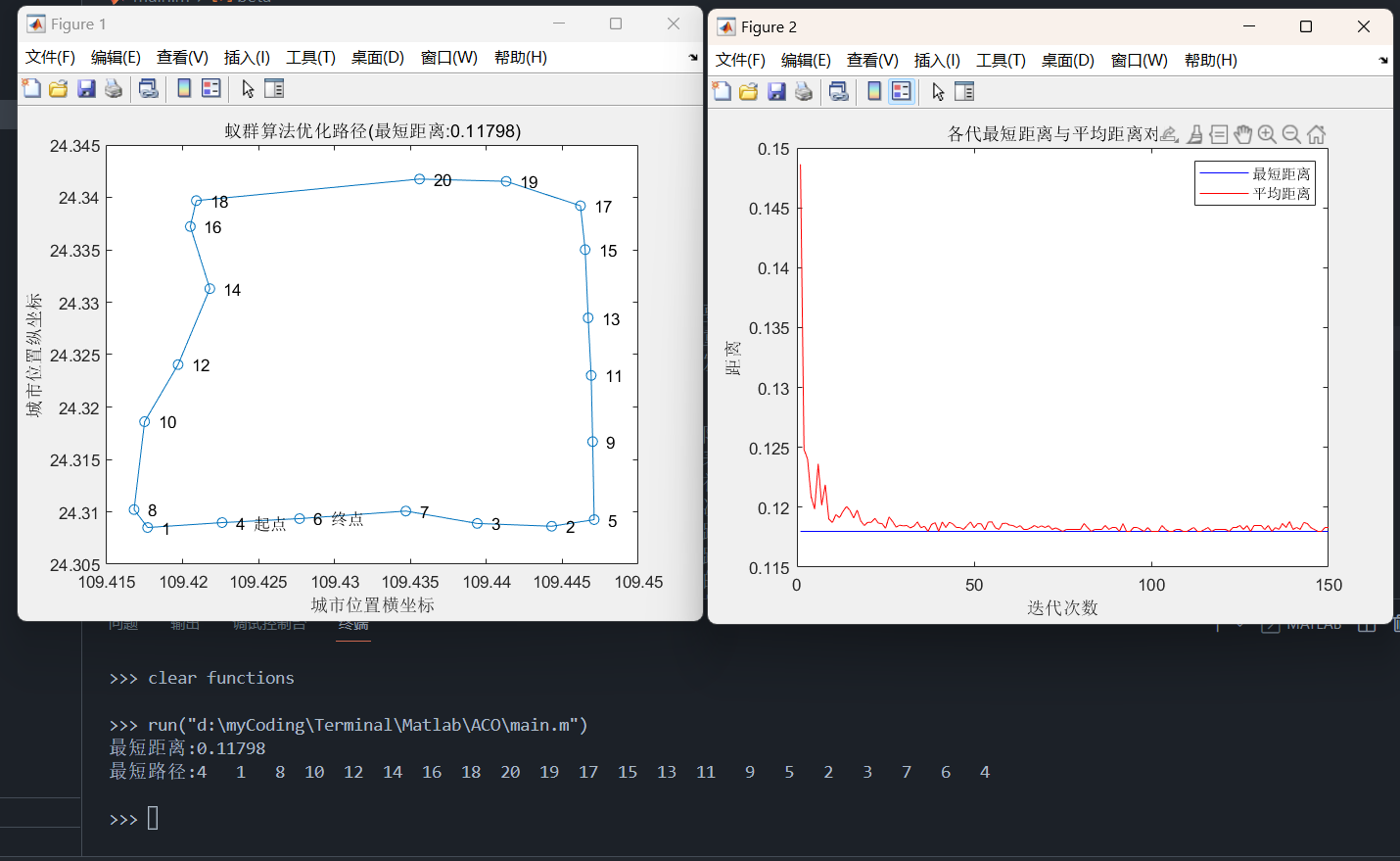
效果如下图所示:
主函数:
%% 旅行商问题(TSP)优化
%% 清空环境变量
clear; clc
%% 导入数据
% load citys_data.mat
load data.mat
citys = data;
%% 计算城市间相互距离
n = size(citys, 1);
D = distance(citys, n);
%% 初始化参数
m = 20; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.2; % 信息素挥发因子
Q = 10; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n, n); % 信息素矩阵
Table = zeros(m, n); % 路径记录表
it = 1; % 迭代次数初值
G = 150; % 最大迭代次数
Route_best = zeros(G, n); % 各代最佳路径
Length_best = zeros(G, 1); % 各代最佳路径的长度
Length_ave = zeros(G, 1); % 各代路径的平均长度
citys_index = 1:n; % 给城市编号
%% 迭代寻找最佳路径
while it <= G
% 随机产生各个蚂蚁的起点城市
Table(:, 1) = randi([1 n], m, 1);
for i = 1:m
for j = 2:n
tabu = Table(i, 1:(j - 1)); % 已访问的城市集合(禁忌表)
allow = citys_index(~ismember(citys_index, tabu)); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end), allow(k))^alpha * Eta(tabu(end), allow(k))^beta;
end
% 轮盘赌法选择下一个访问城市
Table(i,j) = allow(find(cumsum(P/sum(P)) >= rand, 1));
end
end
% 计算各个蚂蚁的路径距离
Length = getPathLength(m, n, Table, D);
% 计算最短路径距离及平均距离
[min_Length, min_index] = min(Length);
Length_ave(it) = mean(Length);
Route_best(it, :) = Table(min_index, :);
if it == 1
Length_best(it) = min_Length;
else
Length_best(it) = min(Length_best(it - 1), min_Length);
if Length_best(it) ~= min_Length
Route_best(it, :) = Route_best((it - 1), :);
end
end
% 更新信息素
Tau = updateTau(Tau, rho, m, n, Table, Q, Length);
it = it + 1;
end
%% 结果显示
[Shortest_Length, index] = min(Length_best);
Shortest_Route = Route_best(index, :);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
%% 绘图
figure(1)
plot([citys(Shortest_Route, 1); citys(Shortest_Route(1), 1)],...
[citys(Shortest_Route, 2); citys(Shortest_Route(1), 2)], 'o-');
for i = 1:size(citys,1)
text(citys(i, 1), citys(i, 2), [' ' num2str(i)]);
end
text(citys(Shortest_Route(1), 1), citys(Shortest_Route(1), 2), ' 起点');
text(citys(Shortest_Route(end), 1), citys(Shortest_Route(end), 2), ' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:G, Length_best, 'b', 1:G, Length_ave, 'r-')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')
主函数调用的子函数如下所示:
- distance.m
function D = distance(citys, n)
%distance - 获取城市距离矩阵
%
% Syntax: D = distance(citys, n)
%
% Long description
D = zeros(n, n);
for i = 1:n
for j = 1:n
if i ~= j
D(i, j) = sqrt(sum((citys(i, :) - citys(j, :)).^2));
else
D(i,j) = 1e-4;
end
end
end
end
- getPathLength.m
function Length = getPathLength(m, n, Table, D)
%getPathLength - Description
%
% Syntax: Length = getPathLength(m, n, Table, D)
%
% Long description
Length = zeros(m, 1);
for i = 1:m
Route = Table(i, :);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j), Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
end
- updateTau.m
function Tau = updateTau(Tau, rho, m, n, Table, Q, Length)
%updateTau - 更新信息素
%
% Syntax: Tau = updateTau(Tau, rho, m, n, Table, Q, Length)
%
% Long description
Delta_Tau = zeros(n, n);
for i = 1:m
for j = 1:(n - 1)
Delta_Tau(Table(i, j),Table(i, j+1)) = Delta_Tau(Table(i, j),Table(i, j + 1)) + Q/Length(i);
end
Delta_Tau(Table(i, n),Table(i, 1)) = Delta_Tau(Table(i, n),Table(i, 1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
end
参考文献
智能优化算法及其MATLAB实例 / 包子阳,余继周,杨杉编著.



