通过例子学习粒子群优化算法
粒子群优化算法
简介
粒子群优化算法(Particle Swrm Optimization, PSO)是由美国的J.Kenney和R.C.Eberhart于1995年提出。它是基于鸟群社会行为的模拟而发展起来的一种群体随机优化技术。目前已被用于函数优化、神经网络、数据挖掘和模糊系统等。
优化问题:
使用粒子群优化算法来解决以上的优化问题。
主要的变化公式:
原理
粒子群优化算法来源于对鸟类群体活动规律性的研究,进而利用群体智能建立一个简化的模型。它模拟鸟类的觅食行为,将求解问题的搜索空间比作鸟类的飞行空间,将每只鸟抽象成一个没有质量和体积的粒子,用它来表征问题的一个可行解,将寻找问题最优解的过程看成鸟类寻找食物的过程,进而求解复杂的优化问题。粒子群算法于其他进化算法一样,也是基于“种群”和“进化”的概念,通过个体间的协作与竞争,实现对复杂空间最优解的搜索。同时,它又不像其他进化算法那样对个体进行交叉、变异、选择等进化算子操作,而将群体中的个体看作在\(D\)维搜索空间中没有质量和体积的粒子,每个粒子以一定的速度在解空间运动,并向自身历史最佳位置\(p_{best}\)和群体历史最佳位置\(g_{best}\)聚集,实现对候选解的进化。粒子群算法具有很好的生物社会背景而易于理解,由于参数少而容易实现。
特点
粒子群算法本质是一种随机搜索算法,它是一种新兴的智能优化技术。该算法能以较大概率收敛于全局最优解。实践证明,它适合在动态、多目标优化环境中寻优,与传统优化算法相比,具有较快的计算速度和更好的全局搜索能力。
-
粒子群算法是基于群智能理论的优化算法,通过群体中粒子间的合作与竞争产生的群体智能指导优化搜索。粒子群算法是一种高效的并行搜索算法。
-
粒子群算法与遗传算法都是随机初始化种群,使用适应值来评价个体的优劣程度和进行一定的随机搜索。但粒子群算法根据自己的速度来决定搜索,没有遗传算法的交叉与变异。
-
由于每个粒子在算法结束时仍保持其个体极值,因此将粒子群算法用于调度和决策问题可以给出多种有意义的方案。
-
粒子群算法特有的记忆使其可以动态地跟踪当前搜索情况并调整其搜索策略。另外,粒子群算法对种群的大小不敏感,即使种群数目下降时,性能下降也不是很大。
算法流程
粒子群算法基于“种群”和“进化”的概念,通过个体间的协作与竞争,实现复杂空间最优解的搜索,其流程如下:
-
初始化粒子种群,包括种群规模\(N\),每个粒子的位置\(x_i\)速度\(v_i\).
-
计算每个粒子的适应值\(fit[i]\)
-
对每个粒子,用它的适应值\(fit[i]\)和个体极值\(p_{best}(i)\)比较。如果\(fit[i] < p_{best}(i)\),则用\(fit[i]\)代替\(p_{best}(i)\).
-
对每个粒子,用它的适应值\(fit[i]\)和全局极值\(g_best\)比较。如果\(fit[i]\),则用\(fit[i]\)替换\(g_{best}\).
-
迭代更新粒子的速度\(v_i\)和位置\(x_i\).
-
进行边界条件处理。
-
判断算法终止条件是否满足:若是,则结束算法并输出优化结果;否则返回步骤(2).
流程图如下:
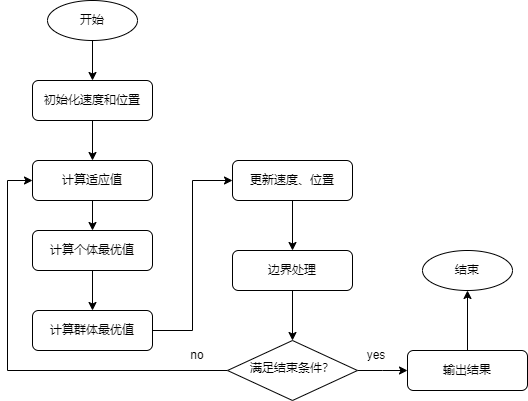
初始化参数
主要的参数:
-
变量维度
-
速度惯性
-
自学学习因子
-
社会学习因子
-
迭代次数
-
速度的下界
-
速度的上界
-
位置的下界
-
位置的上界
次要的参数:
-
种群大小
-
粒子的历代适应值
-
当代全局最优适应值
-
当代全局最优解
-
速度权重衰减系数
-
绘图变量
%% 参数初始化
D = 10; % 函数的维度,即有D个x
N = 50; % 粒子的个数
G = 600; % 迭代次数
w = 0.8; % 速度权重
h = (0.8 - 0.2) / G; % 速度权重衰减系数
c1 = 2; % 自学学习因子
c2 = 2; % 社会学习因子
Xmin = -3; % 变量的下界
Xmax = 3; % 变量的上界
Vmin = -3; % 粒子变化速度的下界
Vmax = 3; % 粒子变化速度的上界
x = Xmin + rand(N, D) * (Xmax - Xmin); % 给种群中的每一个粒子初始化位置
v = Vmin + rand(N, D) * (Vmax - Vmin); % 给种群中的每一个粒子初始化速度
p = x; % 初始化粒子
pbest = fitness(x); % 当代粒子的适应值
[gbest, index] = max(pbest); % 最高适应值
g = x(index, :); % 最优个体
gplot = zeros(G, 1); % 记录每一代最高适应值
gplot(1) = gbest;
附录
%% 粒子群优化算法解决函数优化问题
%% 清屏
clear; clc;
%% 参数初始化
D = 10; % 函数的维度,即有D个x
N = 50; % 粒子的个数
G = 600; % 迭代次数
w = 0.8; % 速度权重
h = (0.8 - 0.2) / G; % 速度权重衰减系数
c1 = 2; % 自学学习因子
c2 = 2; % 社会学习因子
Xmin = -3; % 变量的下界
Xmax = 3; % 变量的上界
Vmin = -3; % 粒子变化速度的下界
Vmax = 3; % 粒子变化速度的上界
x = Xmin + rand(N, D) * (Xmax - Xmin); % 给种群中的每一个粒子初始化位置
v = Vmin + rand(N, D) * (Vmax - Vmin); % 给种群中的每一个粒子初始化速度
p = x; % 初始化粒子
pbest = fitness(x); % 当代粒子的适应值
[gbest, index] = max(pbest); % 最高适应值
g = x(index, :); % 最优个体
gplot = zeros(G, 1); % 记录每一代最高适应值
gplot(1) = gbest;
%% 开始迭代
for it = 2:G
v = w*v + c1*rand*(p - x) + c2*rand*(g - x); % 更新速度
v(v < Vmin) = Vmin; % 处理下界
v(v > Vmax) = Vmax; % 处理上界
x = x + v; % 更新位置
x(x < Xmin) = Xmin; % 处理下界
x(x > Xmax) = Xmax; % 处理上界
pbest_curent = fitness(x); % 计算当代适应值
[gbest_curent, index] = max(pbest_curent);
g_curent = x(index, :);
index = find(pbest_curent > pbest);
pbest(index) = pbest_curent(index);
p(index, :) = x(index, :);
if gbest_curent > gbest
gbest = gbest_curent;
g = g_curent;
end
gplot(it) = gbest;
w = w - h;
end
plot(gplot);
title('适应值变化曲线');
disp(['最优解为: ' num2str(g)]);
disp(['最优值为: ' num2str(f(g))]);



