非极大值抑制

1  算法原理

 　　非极大值抑制算法（Non-maximum suppression, NMS）抑制不是极大值的元素，搜索局部的极大值。这个局部代表的是一个邻域，邻域有两个参数可变，一是邻域的维数，二是邻域的大小。

　　在3领域中，假设一个行向量的长度为w，从左向右，由第一个到第w个和其3领域中的数值进行比对。

　　（1）情况1：如果某个i大于i+1并且小于i-1，则其为一个绝不最大值，同时也就意味着i+1不是一个局部最大值，所以将i移动2个步长，从i+2开始继续向后进行比较判断。

　　（2）情形2：如果某个i不满足上述条件（1），则将i+1赋值给i，继续对新的i进行比对。当比对到最后一个w时，直接将w设置为局部最大值。算法流程如下图所示。

　　　　

 

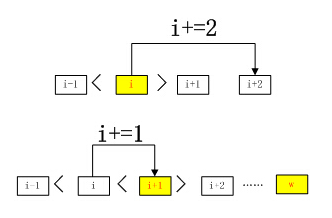
2 3邻域情况下NMS函数的实现

 //求解局部最大值
 //输入参数a:数组a
//输入参数n：数组的维数
int mynms(int a[],int n)
{
    int i = 2;
    while(i < n){
        if((a[i]>a[i+1])||(a[i]= a[i+1])){
            if((a[i]>a[i-1])||(a[i]= a[i-1])){
                return i;
            }
            i = i + 1;
        }
        else{
            i = i + 2;
        }
    }
   //没有找到局部最大值，返回-1  
    return -1;
}

3 3邻域情况下NMS函数的调用示例

int main()
{
    //创建数组a
    int n = 6;
    int a[n] = {1,6,3,5,4,6};
    //求局部最大值的索引值
    int index = mynms(a,6);
    //找到局部最大值时打印出局部最大值
    if(index != -1){
        printf("第一个局部最大值:\n    a[%d] = %d\n",index,a[index]);
    }
    return 0;
}