数据结构——二叉树、二叉查找树

参考：Mark Allen Weiss 著《数据结构与算法分析——C语言描述》（第二版）

主要内容：二叉树及二叉查找树

一、二叉树

1 二叉树定义

　　二叉树是一棵每个节点都不能有多于两个儿子的树

2 实现

　　2.1 实现思路

　　　　因为一个二叉树最多有两个儿子，所以我们可以用指针直接指向它们。

　　2.2 实现代码

typedef struct TreeNode *PtrToNode;
typedef struct PtrToNode Tree;

struct TreeNode
{
    int Element;
    Tree Left;
    Tree Right;
};

二、二叉查找树

1 二叉查找树的定义

　　二叉查找树是一棵特殊的二叉树。对于数中的每个节点X，它的左子树中所有关键字值小于X的关键字；

而它的右子树中所有关键字值大于X的关键字。图1中，只有左边的二叉树是二叉查找树。因为右边的树在关键字为6的节点的左子树中有个节点的关键字为7，大于6。

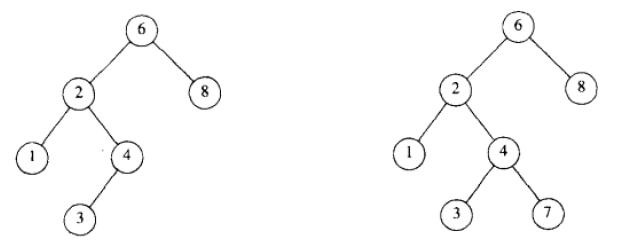
　　　　　　　　　　　　　　　　　　　　　　　　图1 两棵二叉树

2 基本操作

　　函数声明代码

 1  1 #ifndef BINARY_SEARCH_TREE_H_INCLUDED
 2  2 #define BINARY_SEARCH_TREE_H_INCLUDED
 3  3 #include <stdio.h>
 4  4 #include <stdlib.h>
 5  5 
 6  6     struct TreeNode;
 7  7     typedef struct TreeNode *Position;
 8  8     typedef struct TreeNode *SearchTree;
 9  9 
10 10     SearchTree MakeEmpty(SearchTree T);
11 11     Position Find(int X,SearchTree T);
12 12     Position FindMin(SearchTree T);
13 13     Position FindMax01(SearchTree T);
14 14     Position FindMax02(SearchTree T);
15 15     SearchTree Insert(int X,SearchTree T);
16 16     SearchTree Delete(int X,SearchTree T);
17 17     void Retrieve01(Position P);
18 18     int Retrieve(Position P);
19 19 #endif // BINARY_SEARCH_TREE_H_INCLUDED

　　2.1 初始化操作（MakeEmpty）

　　　　2.1.1 实现思路

　　　　　　创建一个空树。

　　　　2.1.2 伪代码　　

 1 /*建立一棵空树的例程*/
 2 SearchTree MakeEmpty(SearchTree T)
 3 {
 4     if(NULL != T)
 5     {
 6         MakeEmpty(T->Left);
 7         MakeEmpty(T->Right);
 8         free(T);
 9     }
10     return NULL;
11 }

　　2.2 查找操作（Find）

　　　　2.2.1 实现思路见图1。

　　　　　　　　　　　　　图2 Find实现思路

　　　　　　注意：一般返回指向树T中具有关键字X的节点的指针，如果这样的节点不存在则返回NULL　　　

　　　　2.2.2 伪代码

 1 /*二叉查找树得到Find操作*/
 2 Position Find(int X,SearchTree T)
 3 {
 4     if(NULL == T)
 5     {
 6         return NULL;
 7     }
 8     if(X < T->Element)
 9     {
10         Find( X,T->Left);
11     }else if(X > T->Element)
12     {
13         Find( X,T->Right);
14     }else{
15         return T;
16     }
17 }

　　　2.2.3 补充

　　　　由Find操作延伸出查找最小值操作（FindMin）和查找最大值操作（FindMax）。

（1）查找最小值操作（FindMin）

　　　　　　基本思路为：从根开始并且只要有左儿子就对左子树进行Find操作，返回值为指向最小值节点的指针。实现代码如下，

 1 /*对二叉查找树的FindMin的递归实现*/
 2 Position FindMin(SearchTree T)
 3 {
 4     if(NULL == T){
 5         return NULL;}
 6     if(NULL == T->Left)
 7     {
 8         return T;
 9     }else{
10         return FindMin(T->Left);
11     }
12 }

（2）查找最小值操作（FindMax）

　　　　　　基本思路为：从根开始并且只要有右儿子就对右子树进行Find操作，返回值为指向最大值节点的指针。实现代码如下，

/*对二叉查找树的FindMax的递归实现*/
Position FindMax01(SearchTree T)
{
    if(NULL == T){
        return NULL;}
    if(NULL == T->Right)
    {
        return T;
    }else{
        return FindMin(T->Right);
    }
}
/*对二叉查找树的FindMax的非递归实现*/
Position FindMax02(SearchTree T)
{
    if(NULL != T){
        while(T->Right != NULL)
        {
            T=T->Right;
        }
    }
    return T;
}

　　2.3 插入操作（Insert）

　　　　2.3.1 实现思路如图3

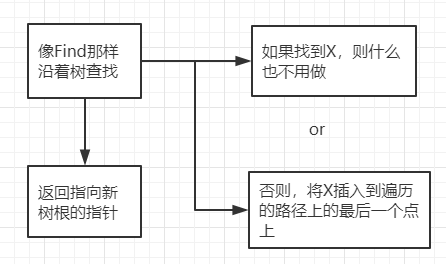
　　　　　　　　　　　　　　　　　　　　　图3 插入操作实现思路

　　　　2.3.2 实现代码如下，

 1 /*插入元素到二叉查找树的例程*/
 2 SearchTree Insert(int X,SearchTree T)
 3 {
 4     if(NULL == T)
 5     {
 6         T = (struct TreeNode *)malloc(sizeof(struct TreeNode));
 7         if( T == NULL )
 8         {
 9             perror("Out Of Space!!!");
10         }else{
11             T->Element = X;
12             T->Left = NULL;
13             T->Right = NULL;
14         }
15     }else if( X > T->Element)
16     {
17         T->Right = Insert( X,T->Right);
18     }else if( X < T->Element)
19     {
20         T->Left = Insert( X,T->Right);
21     }
22     return T;
23 }

　　2.4 删除操作（Delete）

　　　　2.4.1 实现思路如图4

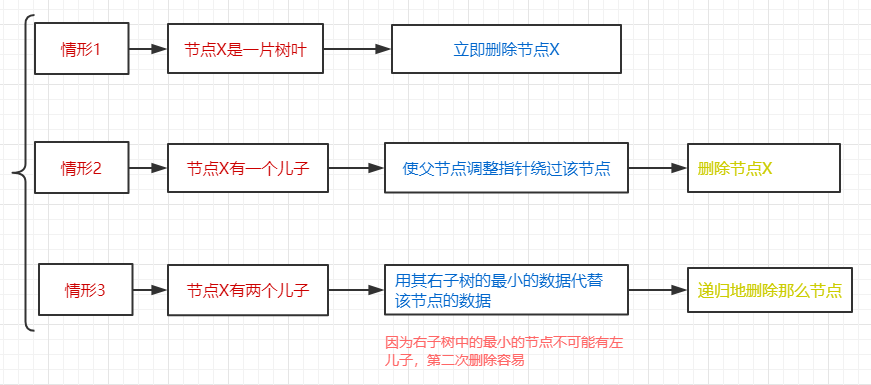
　　　　　　　　　　　　　　　　　　　　　图4 删除操作实现思路

　　　　2.4.2 实现代码如下，

/*二叉查找树的删除例程*/
SearchTree Delete(int X,SearchTree T)
{
    Position TmpCell;
    if(NULL == T)
    {
        perror("Element is not found");
    }else if(X < T->Element)
    {
        T->Left = Delete(X,T->Left);
    }else if(X > T->Element)
    {
        T->Right = Delete(X,T->Right);
    }else{
        if(T->Left && T->Right )
        {
            TmpCell = FindMin(T->Right);
            T->Element = TmpCell->Element;
            T->Right =Delete(T->Element,T->Right);
        }else{
            TmpCell = T;
            if(T->Left == NULL)
            {
                T =T->Right;
            }else if(T->Right == NULL)
            {
                T = T->Left;
            }
        }
      free(TmpCell);
    }
    return T;
}

posted on 2018-08-13 20:12 翠竹09 阅读(1120) 评论(0) 编辑收藏举报