B树

 

B树

并不是心里有b数的b数，而是一种多路平衡查找树。

维基百科对于B的解释

鲁道夫·拜尔（Rudolf Bayer）和 艾华·M·麦克雷（Ed M. McCreight）于1972年在波音研究实验室（Boeing Research Labs）工作时发明了B 树，但是他们没有解释B 代表什么意义（如果有的话）。道格拉斯·科默尔（Douglas Comer）解释说: 两位作者从来都没解释过B树的原始意义。正如我们所见，“balanced”， “broad” 或 “bushy” 可能适合。其他人建议字母“B”代表 Boeing。源自于他的赞助，不过，看起来把B树当作“Bayer”树更合适些

高德纳（Donald Knuth） 在他1980年5月发表的题为“CS144C classroom lecture about disk storage and B-trees”的论文中推测了B树的名字取义，提出“B”可能意味Boeing 或者Bayer 的名字。

 

一棵m阶B树或为空树，或为满足如下特性的m叉树：
（1）树中每个节点最多有m棵子树（即节点最多含有m-1个关键字）

（2）若根节点不是终端节点，则至少有两棵子树（即最少有2个字节点）

（3）除了根节点外的所有非叶子节点至少有 m / 2 向上取整棵子树（即除了根节点以外的所有非叶子节点至少有m / 2 向上取整后-1个关键字）

（4）非叶子节点结构如下：
n  P0  K1  P1  K2 ... Pn Kn

Ki (i = 1, 2, 3,...,n) 为n个关键字，所有Ki < Kj (i < j)

Pi (i = 0, 1, 2, ..., n)为n+1个指向子节点的指针，Pi 所指向子树的所有节点值 均 大于 Ki， 均小于Pj (i < j)所指向的所有子树节点值

（5）所有的叶子节点都出现在同一层上（最后一层），并且不带任何信息

 

 

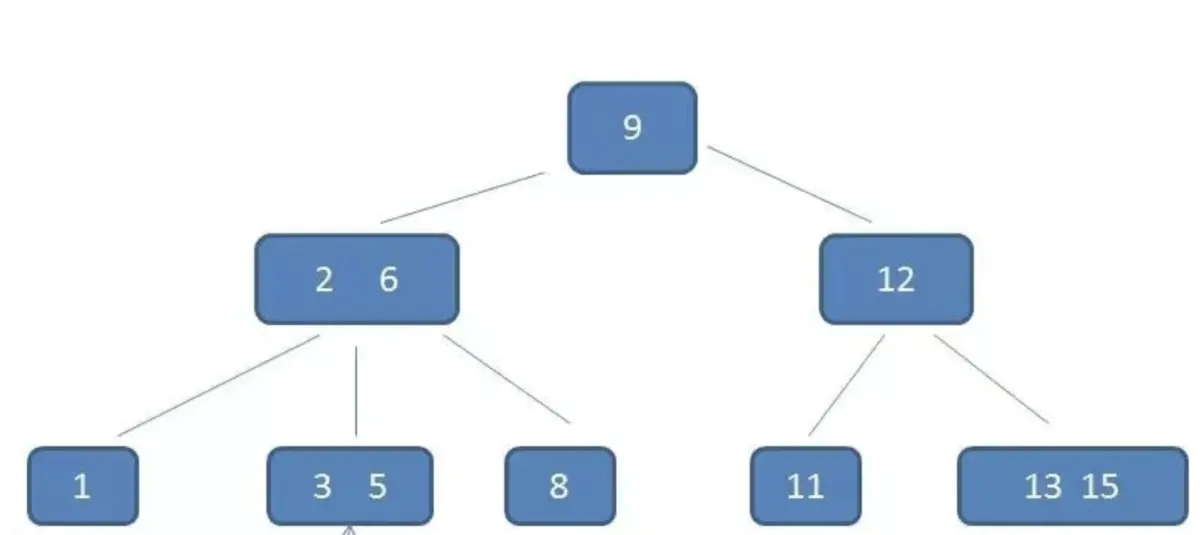
如图是一棵3阶B树（叶子节点没有画出来）

 

一棵有n个关键字，m阶，高度为h的B树，其高度范围是多少？

LOGm(n+1) <= h <= LOG「m/2] ((n+1) / 2) + 1