-
目录结构
-
二叉树
-
二叉排序树
-
平衡二叉树
-
红黑树
-
B树
-
B+树
-
B*树
各种各样的树(上):http://www.cnblogs.com/cuglzf/p/8657698.html
各种各样的树(中):http://www.cnblogs.com/cuglzf/p/8661674.html
在上篇中,介绍了二叉树、二叉排序树和平衡二叉树,中篇介绍了红黑树,这篇文章介绍B数、B+树和B*树。
5.B树
大家说的B树、B-树、B-Tree说的是同一种树。
5.1为什么出现B树
在前面介绍的不管是平衡二叉树还是红黑树,每个节点最多只有两个分支,都是对二叉树的改进,因此当节点的孩子节点增多时,一个节点就能储存更多的信息,针对多路优化的树就应运而生,不管是B树、B+树还是B*树都是多分支的树。
磁盘在进行数据读写的过程中非常耗时,如果读写一次能尽可能多的得到数据,如果能减少I/O次数就能会大幅度提高性能。而B树每个节点尽可能多的存储信息,树的高度就会减少,磁盘利用B树I/O次数就会减少。
5.2 B树的性质
B树是一种平衡多路查找树,一个m阶(要求m>=3)的B树满足下面条件:
1)每个结点至多拥有m棵子树;
2)根结点至少拥有两颗子树(存在子树的情况下);
3)除了根结点以外,其余每个分支结点至少拥有m/2(向上取整)棵子树;
4)所有的叶结点都在同一层上;
5)有k颗子树的分支结点则存在k-1个关键码,关键码按照递增次序进行排列;
5.3 B树的操作
5.3.1 插入元素
B树的插入一定是插入到叶节点。通过搜索找到对应的结点进行插入,那么根据即将插入的结点的数量又分为下面几种情况。
1)如果该结点的关键字个数没有到达m-1个,那么直接插入即可;
2)如果该结点的关键字个数已经到达了m-1个,那么根据B树的性质显然无法满足,需要将其进行分裂。分裂的规则是该结点分成两半,将中间的关键字进行提升,加入到父亲结点中,但是这又可能存在父亲结点也满员的情况,则不得不向上进行回溯,甚至是要对根结点进行分裂,那么整棵树都加了一层。
相比较前面介绍的红黑树,我觉得B树的操作还是很容易的,下面看图来搞懂B树是如何插入元素的。
1.插入元素不分裂
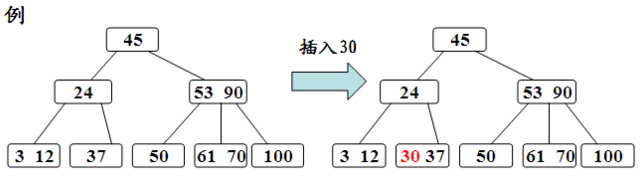
这种情况和二叉树的插入操作一样,上图中插入30,首先30和45比较,比45小则到45的左子树中找,与24比较发现比24大因此到24的右子树中找,与37进行比较比37小,37是叶子节点因此插入到37前面,结束。
2.插入元素分裂
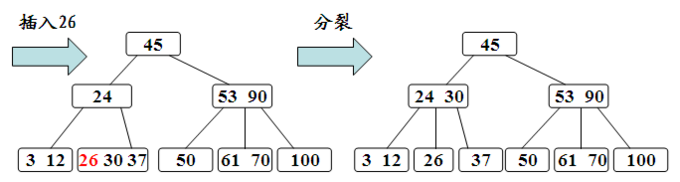
这种情况是当插入元素后,节点不满足B树的性质,需要进行节点的分裂。在上图中插入26后发现26所在的节点不满足3阶B树的性质,需要进行分裂,分裂将30上移并将30的左指针指向26,右指针指向37。如果分裂完成后发现30所在的节点仍然需要分裂,那么用同样的方法进行分裂一直到满足B树的性质为止。
下面看插入的动态图:

5.3.2 删除元素
我们需要先通过搜索找到相应的值,存在则进行删除,删除以后要调整树:
1.如果该结点拥有关键字数量仍然满足B树性质,则不做任何处理;
2.如果该结点在删除关键字以后不满足B树的性质(关键字没有到达ceil(m/2)-1的数量),则需要向兄弟结点借关键字,这有分为兄弟结点的关键字数量是否足够的情况。
1)如果兄弟结点的关键字足够借给该结点,则过程为将父亲结点的关键字下移,兄弟结点的关键字上移;
2)如果兄弟结点的关键字在借出去以后也无法满足情况,即之前兄弟结点的关键字的数量为ceil(m/2)-1,借的一方的关键字数量为ceil(m/2)-2的情况,那么我们可以将该结;
3)点合并到兄弟结点中,合并之后的子结点数量少了一个,则需要将父亲结点的关键字下放,如果父亲结点不满足性质,则向上回溯;
3.其余情况参照BST中的删除。
下面看几个例子来理解删除操作:
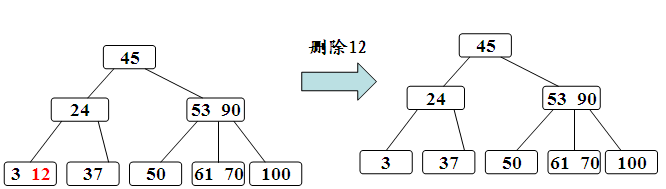
上图删除12,与BST的删除一样。
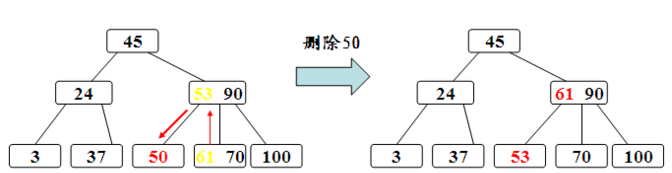
上图是删除50,由于删除50后,50所在节点关键字为空,不满足要求,因此需要从兄弟借用一个关键字,则父节点中的53下移,兄弟节点中的61上移,此时达到了要求。
5.4 B树的应用
B树用于数据库索引,Oracle、Mongo索引采用的就是B树。B树节点存储的不仅是指针,还有data,一个节点储存的索引较少。
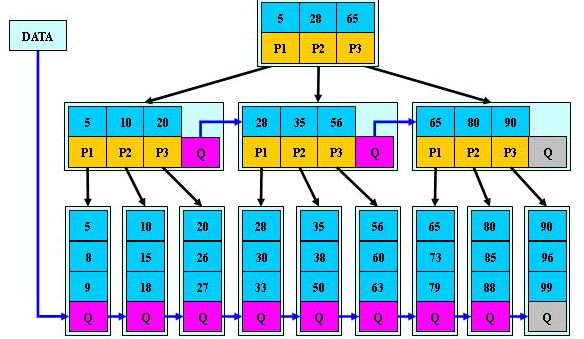
最后看一张3阶B树的图,图中P是指向子节点的指针:
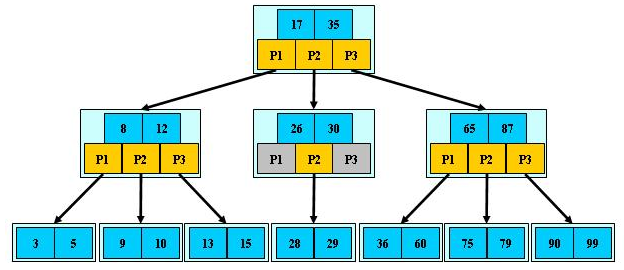
参考:https://www.cnblogs.com/George1994/p/7008732.html
参考:https://www.cnblogs.com/maybe2030/p/4732377.html#_label5
6.B+树
6.1为什么出现B+树
B+树是对B树的改进,因为B树的节点并不是全部装的索引,因此有点浪费空间,B+树改成了除了叶子节点外其他节点中都是关键字。因此B+树只有到达了叶子节点才会命中。
6.2 B+树的性质
B树也是一种平衡多路查找树,定义基本与B树相同,除了下面几点:
1)非叶子节点的子树指针与关键字个数相同;
2)关键字就是对应指针所指子树的关键字的最大值或最小值;
3)B+树比B树多一层叶子节点,包含了数据元素的所有信息,并构成一个有序单链表;
6.3 B+树的操作
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针。
6.4 B+树的应用
因为B+树的操作与B树的相似,这里就不单独讲了,需要的请参考B树的操作。
先看一下3阶的B+树:
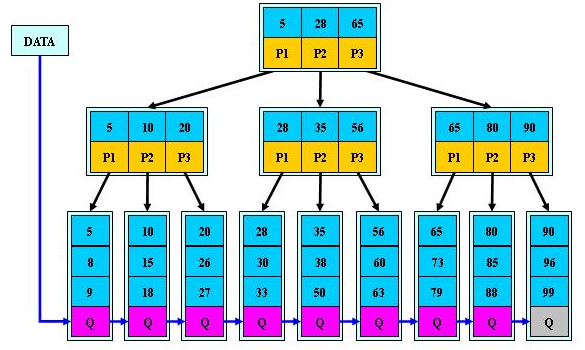
B+树相比B树更加方便,只有达到叶子节点才命中,查询效率相当于二分查找。
MySQL中主要有四种类型的索引,分别为: B-Tree 索引(InnoDB的B-Tree索引实际上是B+树)、 Hash 索引、 Fulltext 索引和 R-Tree 索引。MySQL数据库有两代搜索引擎,MyISAM和InnoDB,这两代引擎区别在于,对于辅助索引的实现原理不一样,并且MyISAM是索引和文件分离的,而InnoDB不是;一般以主键为索引的叫做主索引,而以其他键为索引的叫做辅助索引。InnoDB索引和MyISAM最大的区别是它只有一个数据文件,在InnoDB中,表数据文件本身就是按B+树组织的一个索引结构,这棵树的叶节点数据域保存了完整的数据记录。所以我们又把它的主索引叫做聚集索引。而它的辅助索引和MyISAM也会有所不同,它的辅助索引都是将主键作为数据域。所以,这样当我们查找的时候通过辅助索引要先找到主键,然后通过主索引再找到对于的主键,得到信息。
MySQL两种索引引擎:
1.MyISAM
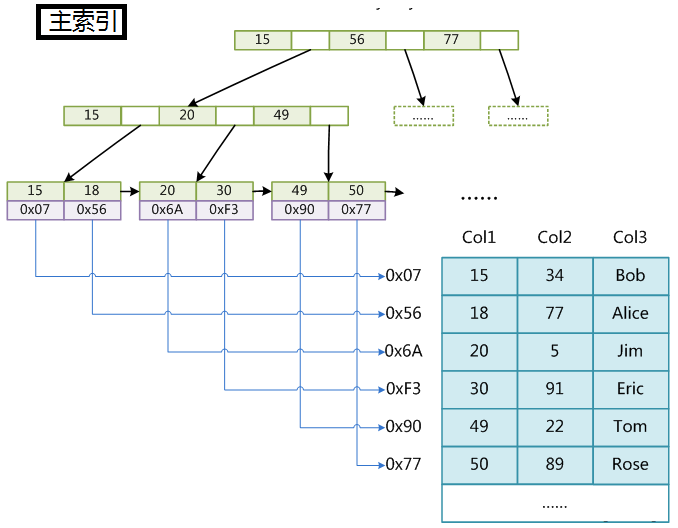
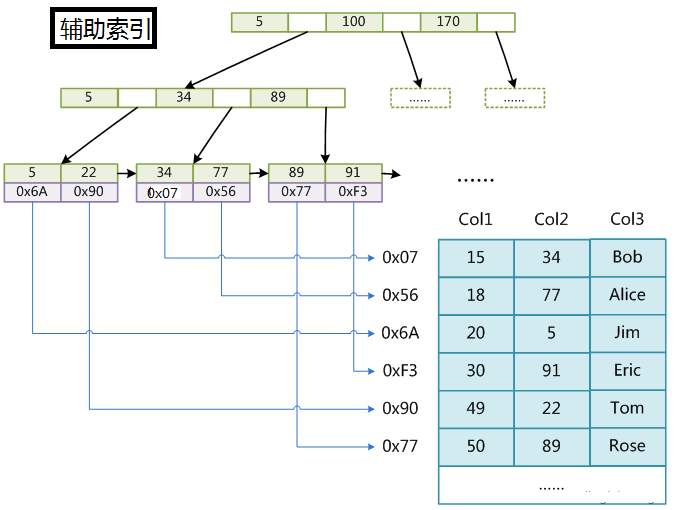
MyISAM索引引擎保存的是主键的地址,查询到了主键,通过主键地址访问主键所在的行。
2.InnoDB
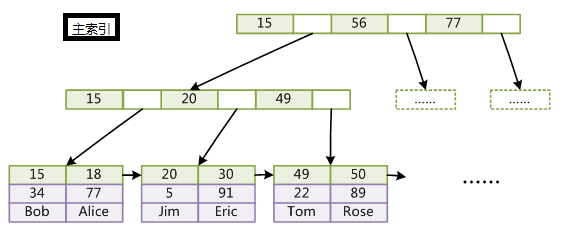
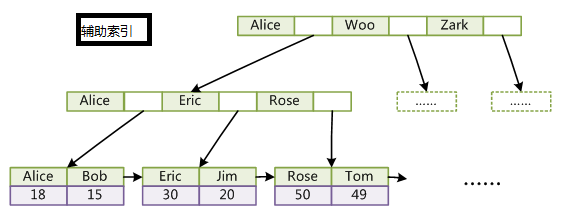
InnoDB与MyISAM不同,InnoDB叶子节点保存了完整的数据,如果主键地址发生改变,只需要改变主索引就好。
参考:https://blog.csdn.net/qq_26768741/article/details/53164202
7.B*树
关于B*树的资料相比较前面几种树来说还是很少的,因此这里就简单介绍一下。
7.1 为什么出现B*树
B*树是对B+树的改进,在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从1/2提高到2/3;
在这比如说当你进行插入节点的时候,它首先是放到兄弟节点里面。如果兄弟节点满了的话,进行分裂的时候从兄弟节点和这个节点各取出1/3,放入新建的节点当中,这样也就实现了空间利用率从1/2到1/3。
7.2 B*树的操作
与B+树的分裂不同,B*树分裂时是当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;所以,B*树分配新结点的概率比B+树要低,空间使用率更高。
下面看一下B*树: