-
目录结构
-
二叉树
-
二叉排序树
-
平衡二叉树
-
红黑树
-
B树
-
B+树
-
B*树
从我们在学习数据结构的时候,各种各样的树弄得我们眼花缭乱,以至于学完了都没弄懂每种树到底是用来干什么的,每种树是怎么插入和删除的,因此我决定好好整理一些常用的树。本文目的在于总结常用的树是如何插入和删除的,目的是学会原理,顺便了解一下每种树大概在什么地方应用,好吧废话不多说,下面开始介绍,我总结了各位大神的博客,找到了很多遍文章介绍每种树的原理,我相信看了你也会弄懂的,我每种树参考的文章都会标注出处。每种树的介绍都按照以下顺序介绍:1)为什么有这种树;2)这种树的性质;3)这种树的操作;4)这种树的应用。
在一篇文章介绍完所有的树有些太长了,全部介绍完感觉看下去的信心都没有了,因此我分为了三篇,上篇介绍二叉树、二叉排序树和平衡二叉树,中篇重点介绍红黑树,下篇介绍B树、B+树和B*树。
1.二叉树
以下所讲的树都是在二叉树的基础上慢慢演变过来的,非常有必要知道什么是二叉树,而且二叉树是最容易实现的,先看下二叉树的概念,这些概念约束虽然很抽象,但是是判断一棵树是否是二叉树的标准。
二叉树的性质:
性质1:二叉树第i层上的结点数目最多为 2i-1 (i≥1)。
性质2:高度为k的二叉树至多有2k-1个结点(k≥1)。
性质3:包含n个结点的二叉树的高度至少为log2 (n+1)。
性质4:在任意一棵二叉树中,若叶结点的个数为n0,度为2的结点数为n2,则n0=n2+1。
上面的定义并不是太严谨,但是很容易理解,还有两种常说的二叉树就是满二叉树和完全二叉树。
满二叉树:
高度为h,并且有2h -1个结点的二叉树,被称为满二叉树,也就是说所有叶子节点都在同一层,其他所有节点都有两个子节点。
完全二叉树:
叶子节点在最后的两层,并且最下面一层的叶子节点全部靠左。
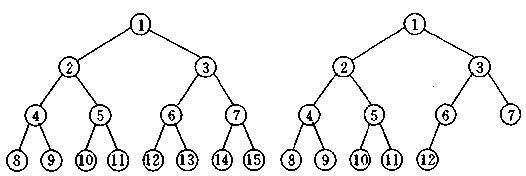
看下面这个图就知道了,左边的是满二叉树,右边的是完全二叉树。
2.二叉排序树
二叉排序树,二叉搜索树(BST),说的是同一种树。
2.1 为什么会出现二叉排序树
我们在学习查找算法的时候,最容易想到的就是二分查找,二分查找的过程其实就是从树的根节点往子节点搜索的过程。当我们在一个有序的数据中插入一个元素或者删除一个元素,对于有序表来说代价非常大,为了保证插入或删除的数据仍然有序,这种代价太高了,降低了查找的效率,因此二叉排序树就出现了。
2.2 二叉排序树的性质
二叉排序树的特点如下:
1)若它的左子树不空,则左子树上所有结点的值均小于它的根结构的值;
2)若它的右子树不空,则右子树上所有结点的值均大于它的根结构的值;
3)它的左子树和右子树都是二叉排序树。
2.3 二叉排序树的操作
2.3.1 查找
二叉树的查找从根节点开始查找,与根节点比较,相等则查找成功返回;若比根节点值小,则在根节点的左子树查找;如果比根节点的值大,则在根节点的右子树查找。
2.3.2 插入元素
若当前的二叉排序树为空,则插入的元素为根节点;
若插入的元素值小于根节点值,则将元素插入到左子树中;
若插入的元素值不小于根节点值,则将元素插入到右子树中。
2.3.3 删除元素
二叉排序树的删除复杂一些,有可能删除节点后改变了树的结构,因此分为三种情况讨论:
- 若删除的是叶子节点,直接删除,再修改其父节点的指针;
- 若删除的只有左子树或右子树,则让其子树直接与其父节点相连即可;
- 若删除的有左右子树,首先找到要删除节点的右子树中的最小值或者左子树的最大值,记录这个节点的父节点,把它的值覆盖要删除的节点;其次删除节点。
下面用图来解释一下删除操作,第一种情况比较简单,很容易理解了,主要是第二种和第三种情况用图来展示
2)若要删除的节点只有左孩子或者右孩子
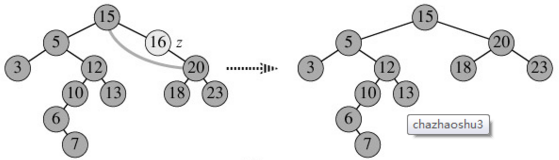
上图要删除16,那么由于16只有一个右孩子,所以把它的右孩子20与15连接,删除16即可。
3)若要删除的节点即有左子树又有右子树

上图是要删除5,首先找到5的右子树的最左孩子6,把6赋给5,就是把5的值给覆盖了,再删除6,此时就回到了上一种情况。
2.4 二叉排序树的应用
二叉排序树的查找相当于二分查找,因此平均时间复杂度是O(lbn),最坏情况下是O(n)。
二叉排序树的缺点很明显,会出现分支退化情况,最极端的情况下只剩下一个分支,那这样查询的时间复杂度就是遍历整个数据的长度了,因此针对二叉排序树的平衡的平衡二叉树就出来了。
参考https://www.cnblogs.com/maybe2030/p/4732377.html
3.平衡二叉树
平衡二叉树(AVL树)
3.1 为什么会出现平衡二叉树
二叉排序树的查询效率非常高,相当于二分查找,查找的次数与树的高度有关,当二叉排序树出现分支退化,树的高度变大,查询时间就会变长。因此平衡二叉树在二叉排序树的基础上控制了树的高度,保证了查询的效率,平衡二叉树就被提出了。
3.2 平衡二叉树的性质
平衡二叉树是基于二叉排序树而构造的,因此在满足二叉树的条件下,最重要的一个性质就是它的左子树的深度和右子树的深度差不能超过1,且它的左右子树都是平衡二叉树。控制平衡就有一个平衡因子,平衡因子(bf)就是结点的左子树的深度减去右子树的深度,那么显然-1<=bf<=1。
3.3 平衡二叉树的操作
之所以我们觉得平衡二叉树难以理解,是因为我们不知道当平衡二叉树失衡以后,如何调整平衡,也就是平衡二叉树的调整平衡策略我们不知道,下面首先需要掌握调整平衡的策略,不管是教材上还是网上都说有4种状态需要调整平衡,RR、RL、LL、LR,到底这表示什么意思,还有如何来调整平衡,如果掌握了这四种情况,那平衡二叉树基本上就掌握了。
在调整平衡时,找离插入节点最近的失衡节点,以下旋转都会有一个旋转中心,旋转中心不动,下图中橙红色为旋转中心,黑色为离插入节点最近的失衡节点。
1)RR型
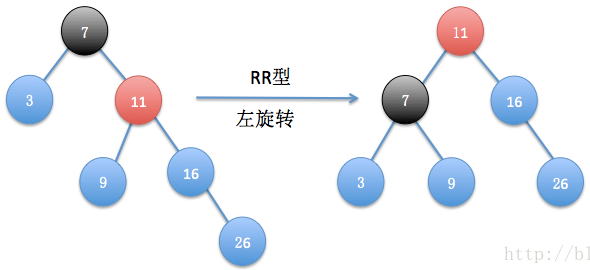
当插入26时,找到离26最近的失衡节点就是7,那如何调整?平衡二叉树是二叉排序树的改进,因此仍然遵守二叉树左子树<根节点<右子树的性质,因此只能让7变成11的左孩子,并将11的左孩子变成7的右孩子,也就是所谓的左旋转。
2)LL型
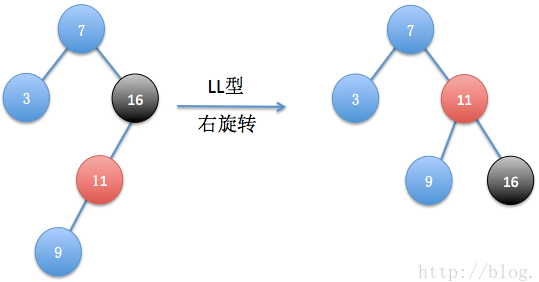
同样LL型与RR型一样,只需要经过一次旋转就可以达到平衡,此时插入9,导致16节点失衡,因此将16节点变为11的右孩子,11节点变为7节点的右孩子,这是就是所谓的右旋。
3)RL型
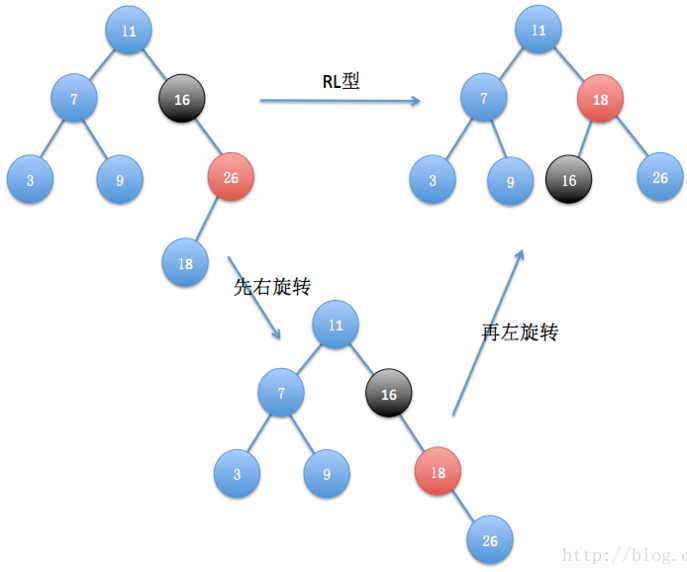
到这里大概大家能看出来了吧,所谓RR、RL这种命名其实就是依据子树的方向命名的,比如上图,16、26、18,26是16的右孩子(Right),18是26的左孩子(Left),因此叫RL型。RL型与前面两种不同需要两次旋转才能平衡,首先经过右旋转,再左旋转。
4)LR型
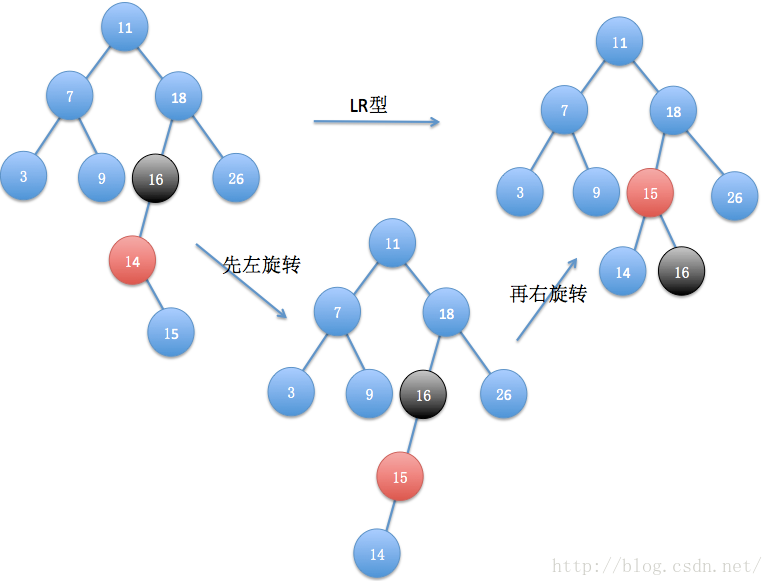
LR型和RL型类似,这里就不重复了。
3.3.1 插入元素
平衡二叉树与二叉树的插入操作一致的,但插入元素后需要调整树的平衡,调整平衡就会出现上面4种情况,然后每次插入根据上面四种情况进行调整。
3.3.2 删除元素
前面已经介绍过了二叉排序树的删除操作,平衡二叉树的删除与之类似,但是删除后需要调整树的平衡,因此在看平衡二叉树的删除操作之前,需要知道二叉排序树是如何删除节点的,所以平衡二叉树的删除操作参考二叉排序树的删除图解,这里只给出过程。
平衡二叉树的删除同样分为三种情况:
1)删除的是叶子节点
直接删除这个叶子节点,并从它的父节点开始判断是否满足平衡,利用递归一直到根节点为止。
2)删除的节点只有左孩子或者右孩子
直接删除此节点,并将此节点的孩子节点作为它的父节点的子节点,再调整平衡。
3)删除的节点有左右孩子
首先找到要删除节点的右子树中的最小值节点或左子树的最大值节点(与平衡二叉树一样),将这个节点的值覆盖要删除节点的值,再将此节点删除,并重新调整树的平衡。
3.3 平衡二叉树的应用
平衡二叉树的查找与树的高度有关,平衡二叉树的查询时间复杂度最坏最好和平均都是(log2n)。Windows进程地址空间管理使用的是平衡二叉树。


