有序表查找
好久没上博客园了,之前说好的一周写一个博客来记录自己的考研计划也落空了。
忙着复习,好久都没有打开电脑,计划也都是写在纸上了。最新开始数据结构的复习才打开了电脑。
开始敲代码的感觉真好。看来我注定是一个码农了。以后还是要多敲敲代码,毕竟是以后吃饭的家伙,三日不练,生疏啊。
不唠叨了,说说今天要写的主题——有序表查找。
(ps 这篇博客是查看程杰老师的大话数据结构后,参考网络上的文章写成的。优缺点和时间复杂度这段完全抄录的程杰老师的原话)。
一、定义
就是字面上的意思,在一张有序表中进行查找。有序表是啥?就是数据按照一定顺序排好的表,而不是一堆杂乱无章的数据。
有序表查找的基本前提就是数据是有序的。
二、几种常见的有序表查找方法
1.折半查找
折半查找(Binary Search) 又称为 二分查找。
折半查找的基本思想是:
将原始数据分为等份的两部分,比较关键字与中间值的大小,如果关键字小于中间值,说明关键字落在左半部分,将查找范围缩小为左半部分,继续折半查找;
如果关键字大于中间值,说明关键字落在右半部分,将查找分为缩小为右半部分,继续折半查找。
通过关键字与中间值的对比,不断缩小查找范围,最终查找数据。原理图如下。
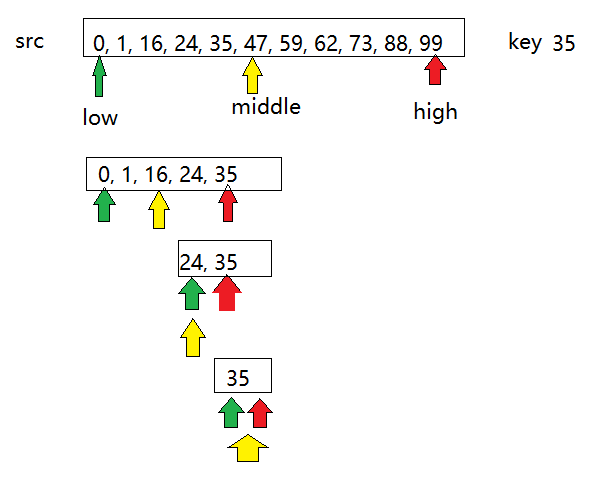
二分法的关键是中间值(也就是分隔)的选取。通过分隔,我们将查找区间缩小,通过不断缩小查找范围,来查找数据。
2、插值查找
二分法将空间分隔的方法非常粗糙,就是讲区间折半。
考虑这样一组数据 {0, 1, 3, 4, 5, 7, 9, 10, 12, 13, 14} ,需要查找的数据是10。
观察这个数组,数组的前后分布存在相对均匀,如果我们使用折半查找,我们共需要查找 4 次,才能查找到数据。这就是不考虑数据分布,粗糙地选取分隔的后果。
为了改进折半查找的缺点,我们重新选取分隔。
经过算法科学家的推到,改进方案如下:
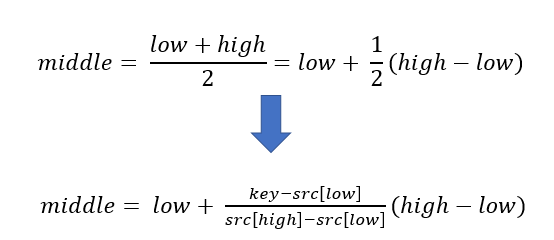
分隔的取值变成上图第二个公式。如果使用第二个公式,上述的查找只需要 1 次就可以轻松查找到。
3、斐波那契查找
斐波那契查找是利用黄金分隔原理来实现的。它的本质和二分查找、插值查找没有区别,都是通过设置分隔,不断将区间缩小,最后查找到关键字的。
与之前两个查找方法相似,斐波那契的不同也是分隔设置的不同,它是通过斐波那契数列来设置的。
斐波那契数列 F = {0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...}
斐波那契查找的一个限制就是,src的数据个数需要是斐波那契数列中的元素之一。
例如src = {0, 1, 16, 24, 35, 47, 59, 62, 73, 88, 99} 。
该数组的个数为11个,11并不是斐波那契数列的元素,13才是,所以需要将数组扩容到13个,即令src[11]=src[12]=99。
斐波那契查找的具体代码如下
/** * 从有序表中查找数据 * @param key 需要查找的数据 * @param src 有序表 * @return */ public static int fobSearch(int key,int[] src){ int length = src.length; int low = 0; //low high 的初始值分别等于有序表索引的最小值和最大值 int high = length-1; int fobInex = 0; // 我们后面需要用到的 斐波那契数组中的索引值 int middle = 0 ; //二分法的分隔值 //使用斐波那契查找的要求 就是有序表的元素个数必须是斐波那契数组元素的值 while(length > getFobonacci(fobInex)){ fobInex ++; } //如果有序表的元素个数不等于斐波那契数组元素的值,则需要在后面补全 int newCapacity = getFobonacci(fobInex);//新数组的大小 if(length < newCapacity){ src = Arrays.copyOf(src, newCapacity); for(int i=length;i<newCapacity;i++){//将后续的数值补全 src[i] = src[i-1]; } } HelpUtils.printIntArray(src);//打印一下补全的数组 while(low <= high){ middle = low + getFobonacci(fobInex-1)-1; if (key < src[middle]) { //如果当前查找记录小于当前分隔记录 high = middle - 1; fobInex = fobInex - 1; } else if (key > src[middle]) { low = middle + 1; fobInex = fobInex - 2; } else{ if (middle < length) { return middle; } else{ return -1; } } } return -1; }
可以看到分隔的选取依赖于斐波那契数列。
三、优缺点和时间复杂度
二分查找、插值查找和斐波那契查找的时间复杂度都是O(logn)。
二分查找的前提条件是需要有序表顺序存储,对于静态查找表,一次排序后不再变化,这样的算法已经比较好了。
但是对于需要频繁执行插入或者删除操作的数据集来说,维护有序表的排序会带来不小的工作量,并不适合使用。
插值查找,对于表长较大,而关键字分布比较均匀的查找表来说,插值查找算法的平均性能要比折半查找好得多。
反之,如果数据中分布类似{0,1,9999,999999}这样极端不均匀的数据,用插值查找未必是最合适的选择。
斐波那契查找,就平均性能而言,要优于二分查找,但是如果是最坏的情况,比如key=0,那么始终在左侧长半区在查找,查找的效率要低于折半查找。
比较关键的一点是,插值、折半都需要进行比较复杂的乘除法运算,
而斐波那契只需要进行简单的加减运算,在海量数据的查找过程中,这种细微的差别可能会影响最终的查找效率。
上述三个有序表查找算法的具体代码都放在我的github上,欢迎查看。


