模拟ic设计第一弹 ——拉扎维第三章 阻抗分析
该系列为模拟ic设计学习笔记,会不定期更新内容。
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
- MOS的两种分析思路
例题:先不考虑RD,求电路的输出阻抗(考虑体效应和沟道长度调制效应等二级效应)

(1)小信号电路分析
把MOS管的模型看作如下:

可以直接列等式求出Rout(Vin接地,输出端加一个电压源Vx,流出电流为Ix)
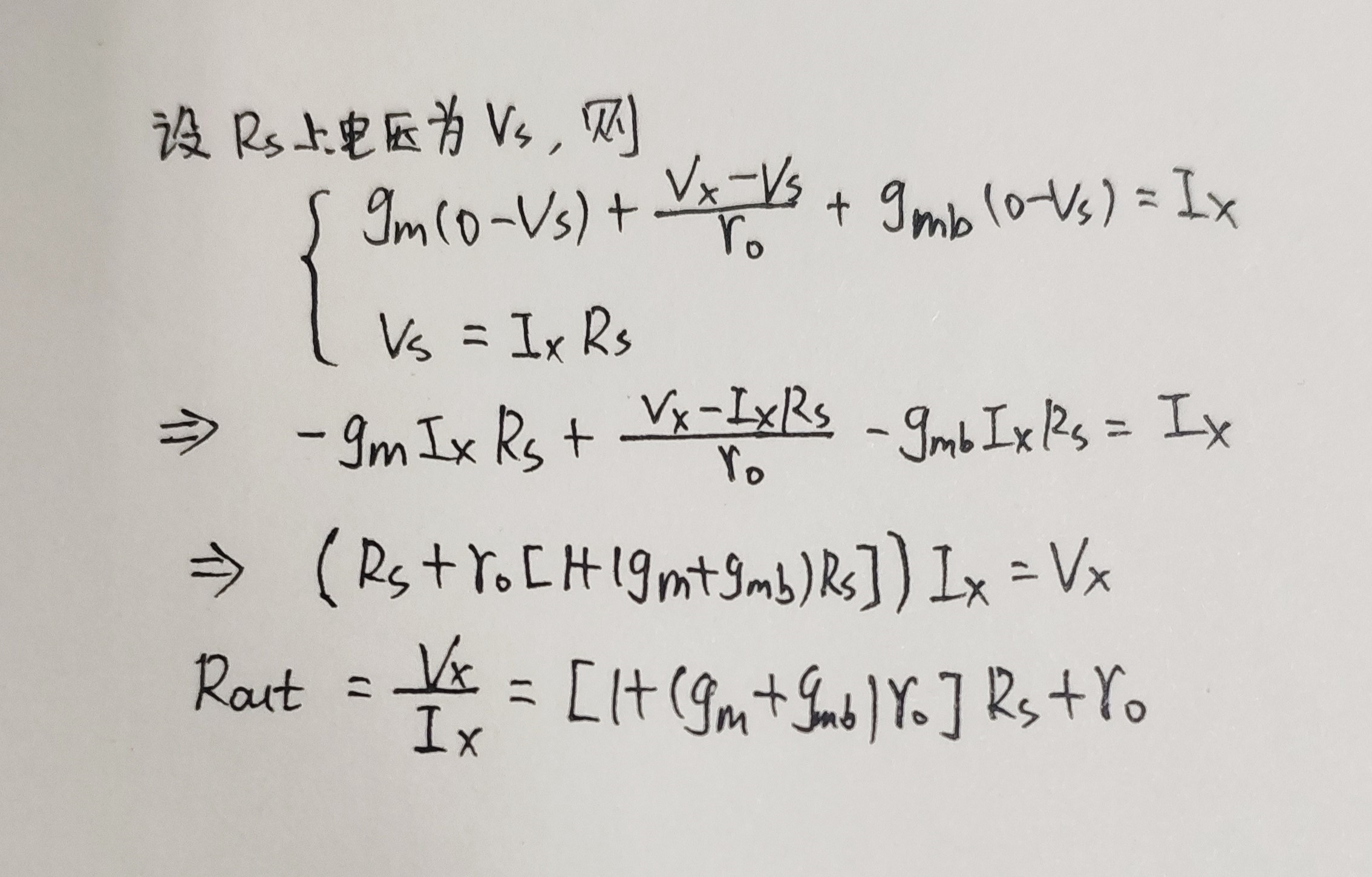
代入小信号模型即为

则求解为

(2)阻抗分析法
注意:此法只能分析漏端变化电压V,求源端电压的变化。不能求解电流关系(原因见下文)
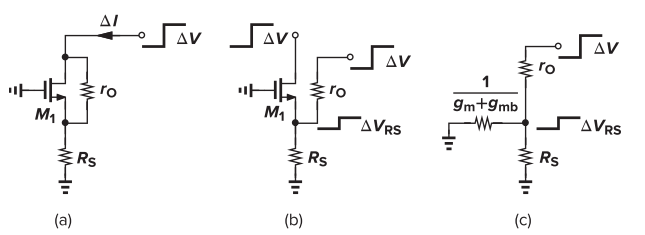
从图(a)开始:在漏端有一个电压变化△V,产生电流变化为△I。最后用△V除以△I得到输出阻抗Rout
对MOS管的理解如下:把MOS看成理想MOS管与ro的并联,其中理想MOS的电流受到电压Vgs的控制,与漏端电压的变化无关。也就是说,对于图(a)中的M1而言(已经看成理想MOS管),从漏端往源端看阻抗为无穷大,而从源端往漏端看阻抗为1/(gm+gmb)。
从漏端往源端看阻抗为无穷大说明此处是断路,而源端往漏端看是有限阻抗,说明有电流从漏端到源端(这样电流就不连续,因此不能求解电流关系)。此处对MOS管进行分析,它可以看成理想受控电流源,电流受Vgs控制,此时栅极接地,因此电流只受源端电压控制。只受一端电压控制的受控电流源可以看作为接地的电阻,此处阻值为1/gm。
对图(b)分析,它将V的影响拆成两条支路,其中MOS管一端的电流变化为0(因ID与VD无关),右边支路则是ro与 Rs和M1源端看进去的阻抗的并联 进行串联,其结果可以等效为图(c)。此时,可以求解漏端电压的变化量:

得到漏端电压变化量之后,不能直接在图(C)中求△I(再次注意此法只能求源端电压的变化)
要求出△I,需要回到图(a),即电阻上产生VRS的电压变化,则
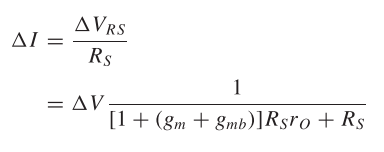
因此,输出阻抗为

注意,此处求出的输出阻抗与用小信号电路的求出的结果完全一致(意思是并不是估算,而是十分精确的结果)
(3)两种方法的讨论
疑问一:方法二中的电流都不连续了,为何能得到与方法一同样的结果
疑问二:两种方法看似比较矛盾,如何统一?
先看两个电路:


我们可以想办法将图一的电路在一定条件下直接等效到图二的电路:
仔细分析图一,假设Rs上的电压为Vs。看受控源gmV1,它的电流值实际上不受Vx的影响,而是与V1有关,即与Vs有关。由于栅极接地,受控源只受电压Vs控制,因此两个电流源均可以看成一端接Vs,另一端接地的电阻,且是并联关系。这样就变成图二(c)的电路。这样就实现了两种方法的统一。
其次,需要分析等效的过程中什么改变了,什么没变。很明显的一点是改变了电路的电流关系,这才是方法二不能用来求解电流关系的根本原因。回到MOS管的基本工作原理,MOS管是由栅源电压控制沟道电流的跨导器件,而沟道电流是由漏端流向源端,此电流与漏端电压无关却是从漏端流出的。而受控源等效为接地电阻改变了电流关系。
更重要的一点是找出什么量没变,那就是M1源端电压的变化量没变,分析图一中的受控源可以发现,两个受控源的电流方向实际上是朝上的,换句话说,从节点Vs看,两个受控源与Rs一样电流都是流出节点的(注意,此处认为受控源实际电流方向是流出节点的,至于流向哪儿可以认为是地,通过等效为接地电阻来看,此处不要纠结电流流向哪儿,因为等效本身就改变了电流关系),这也再次等效成图二(c)。因此两个电路的串并联关系实际上是相同的,因此可以得到相同的分压关系,源端电压的变化量就是相同的了。
此处说明,在漏端有一个电压变化量,求源端的电压变化量用方法二更加合适。
此时又引入一个新的问题,为何小信号电路是对的?即图一所示的电路为何没问题?
方法二是从阻抗的角度进行分析(从漏端往源端看阻抗为无穷大,而从源端往漏端看阻抗为1/(gm+gmb)),因此称为阻抗分析法。而小信号电路实际上是从电流关系入手,通过KCL方程联系起各个关系量。回到方法一的推导上:
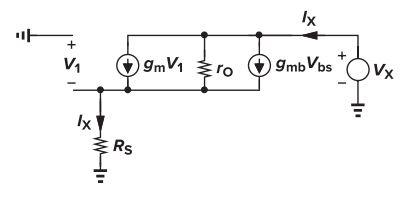

因为受控源电流gmVgs,即沟道电流,认定的方向是从漏端流向源端(实际方向与Vgs的正负有关),因此通过节点电流方程可以的得到Vx与Ix的关系式。



