365. Water and Jug Problem

▶ 倒水问题。我们有两个容积分别为 a 和 b 的桶，请问是否能通过相互倾倒的方式量出体积为 c 的水。

▶ 断言：若 c 满足 0 < c ≤ a + b 且 c = k · (a, b)（k为正整数，()为取最大公约数），则体积为 c 的水可以量出。

● 一个优美的证明，原视频 https://www.youtube.com/watch?v=0Oef3MHYEC0。简单的说明：

■ 我们做如下图 1 的一张棋盘，两轴分别标有 0, 1, ..., a 和 0, 1, ..., b（图中取 a = 5, b = 3，两者相对大小没有影响），并且画有 x + y == C（常数）的斜线。那么，该棋盘中中任意一个格点就可以代表当前两个水桶中的水量的状态。

■ 对于如图 2 中的一个格点 P(3, 2)，它代表现在 5L 的桶中装有 3L 水，3L 的桶中装有 2L 水。那么现在从 P 出发有 6 种路径，如 6 个箭头所示，水平两个分别表示装满或放空 5L 的桶，竖直两个表示装满或放空 3L 的桶，斜向两个表示两个桶之间相互倾倒。注意每次转移都必须沿着某个方向走到尽头，即理论上可达的中间状态只有边框一圈，而没有像 P 点这样的中间点。

■ 图 3 演示了两种从空桶 (0, 0) 开始到量出 4L 的水 (4,0)（实际上只要某一个坐标变成 4 均可） 的过程，分别为蓝线和红线。可见这两条路径便利了所有的状态。

　　　　　　　　　　

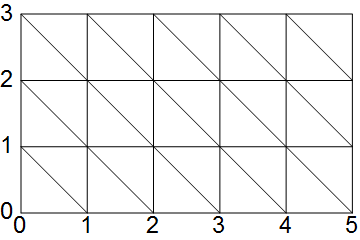
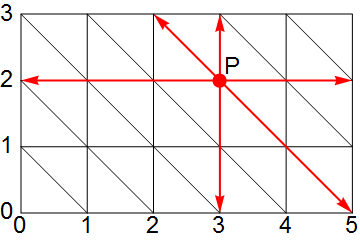
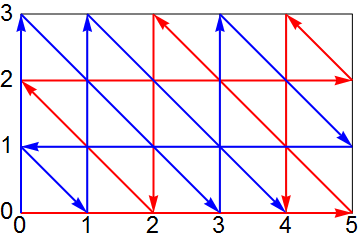
　　　　　　　　　　　　图 1　　　　　　　　　　　　　　　　　　　　　　　　图 2       　　　　　　　　　　　　　　　　　　　　　　图 3

 ■ 图 4 演示了当 a = 6, b = 4 时的情况，一条路径无法遍历所有的状态点。当 a 与 b 不互素的时候就会有空隙，跨度等于 a 与 b 的最大公约数（后面证明）。

　　　

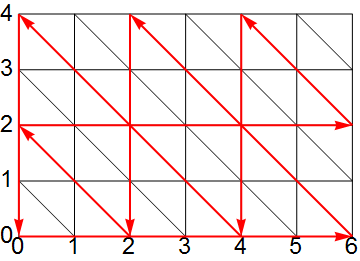
　　　　　　　　　　　　图 4

■ 如图 5 和图 6 所示，考虑从横轴上一点开始，做一个简单的变换：(x, 0) (x ＜ b) → (0, x) → (a, x) → (x + a  - b, 0)，(x, 0) (x ≥ b) → (x - b, b) → (x - b, 0)，即 x = (x + a - b) % a 。

① 若 a 与 b 互素，则 (a - b, a) = 1，对于任意的 x ∈ D₁^a，x 在该变换下生成的子群等于 D₁^a 本身，即 x 总能通过这种变化遍历所有的状态（同理能遍历所有D₁^b）。

② 若 a 与 b 不互素，则 x 在该变换下一共可以生成 (a, b) 个子群，分别为 G_i ={ i + (a, b) · k, k∈N* }（即商群 Z / ((a, b)Z)）。经过原点（初始状态）的只有 G₀，即我们只能遍历 G₀ 中的所有状态。

　　　　　　

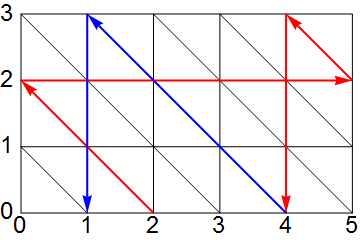
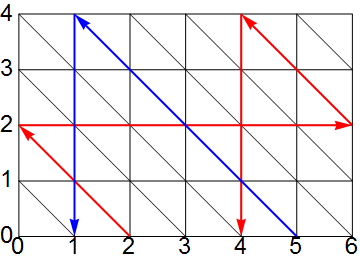
　　　　　　　　　　　　图 5　　　　　　　　　　　　　　　　　　　　　　　图 6

● 代码， 2 ms，本题的解答转化为求 a 与 b 的最大公约数，使用辗转相除法，这里只记一个比较骚的递归方法。一行求解法的代码没有找到，以后补充。

class Solution
{
public:
    bool canMeasureWater(int x, int y, int z)
    {
        if (x + y < z)
            return false;
        if (x == z || y == z || x + y == z) return true;
        return !(z % gcd(x, y));
    }
    int gcd(int a, int b)
    {
        return b ? gcd(b, a % b) : a;
    }
};