42. Trapping Rain Water

▶ 一个有趣的算法题。给定一个非负数数组，把数组中各元素看做是宽度为 1，高度为其值的砖块，求这些砖块最大能盛多少水。如给定数组 [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]，则水量为 6。参考原题答案 https://leetcode.com/problems/trapping-rain-water/solution/

　　

● 代码，598ms 。暴力枚举，对于每个格子，搜索其左右两侧最高的高度，两高度中的较小者与该格子自身高度的差即为该格子盛水量。

class Solution
{
public:
    int trap(vector<int>& height)
    {
        const int size = height.size();
        int ans, i, j, max_l, max_r; 
        for (ans = 0, i = 1; i < size - 1; i++)
        {
            max_l = max_r = 0;
            for (j = i; j >= 0; max_l = max(max_l, height[j--])); 
            for (j = i; j < size; max_r = max(max_r, height[j++]));
            ans += min(max_l, max_r) - height[i];
        }
        return ans;
    }
};

● 代码，12 ms，动态规划。从原数组中得到一个单调不减序列和一个单调不增序列，两序列的交集即为装水量。

　　

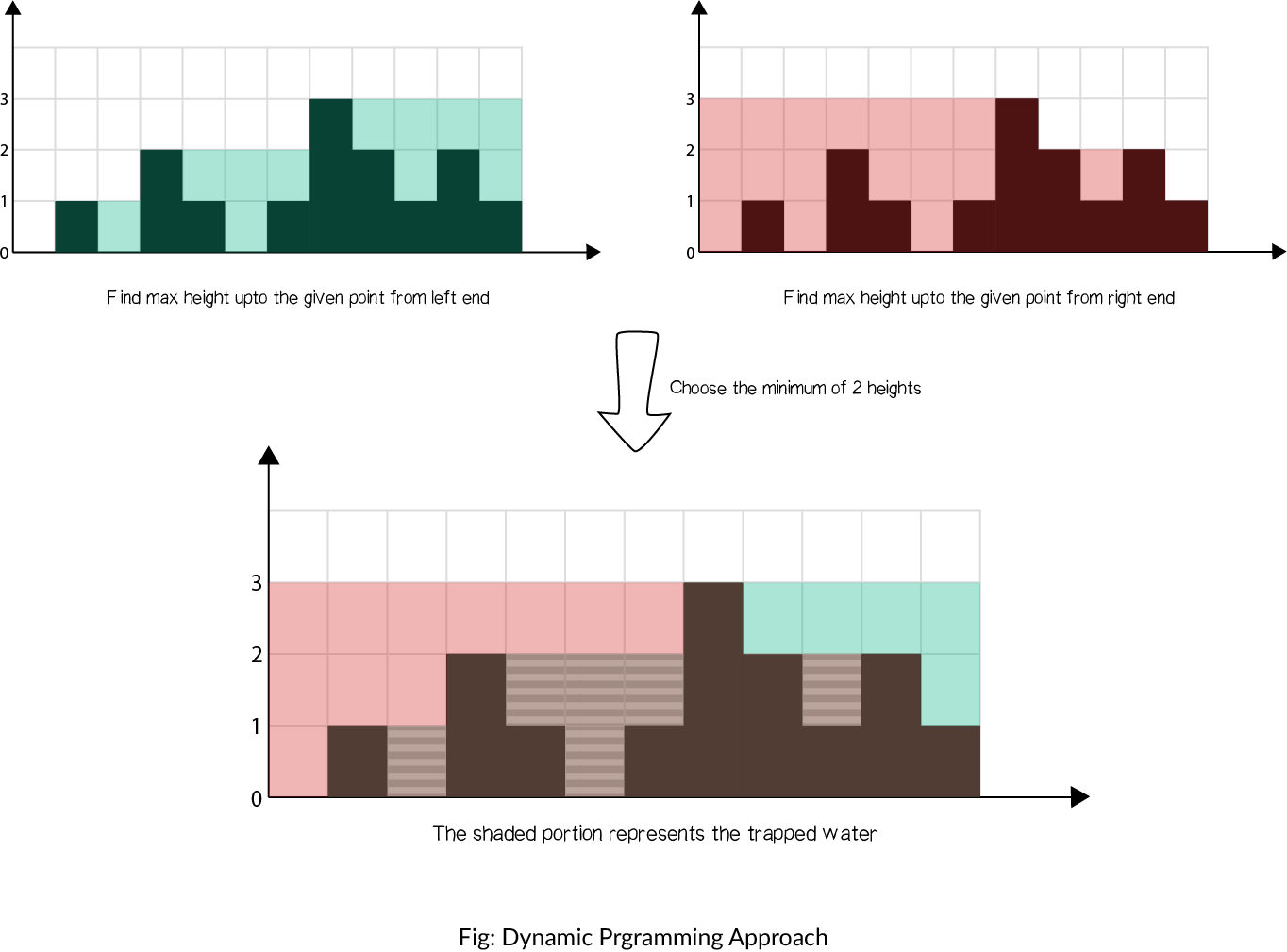
class Solution
{
public:
    int trap(vector<int>& height)
    {
        if (height.size() == 0)
            return 0;
        const int size = height.size();
        vector<int> left_max(size), right_max(size);
        int ans, i;
        for (ans = 0, left_max[0] = height[0], i = 1; i < size; i++)
            left_max[i] = max(height[i], left_max[i - 1]);
        for (right_max[size - 1] = height[size - 1], i = size - 2; i >= 0; i--)
            right_max[i] = max(height[i], right_max[i + 1]);
        for (i = 1; i < size - 1; i++)
            ans += min(left_max[i], right_max[i]) - height[i];
        return ans;
    }
};

● 代码，13 ms，神奇的双指针法。简单的说明：lp 从左向右扫描，并且不断记录目前为止最高坎的高度，当遇到高度降低时发生积水，向 ans 添加本格的积水量（本格积水量等于最高高度减去当前高度）；rp 从右向左扫描，工作方式类似。注意每次搜索下一格之前要先对 candidatex[ lp ] 和 candidatex[ rp ] 做一个比较，只在较低者那边进行上述维护和加值操作，这是为了使最后 lp 和 rp 相遇时汇合于整个数组的最高高度处，此时以该最高高度为分水岭，其左右两边的积水都已经算完，可以返回答案。

class Solution
{
public:
    int trap(vector<int>& height)
    {
        int lp, rp, ans, lpmax, rpmax;
        for (ans = lpmax = rpmax = lp = 0, rp = height.size() - 1; lp < rp;)
        {
            if (height[lp] < height[rp])
            {
                height[lp] >= lpmax ? (lpmax = height[lp]) : (ans += lpmax - height[lp]);
                lp++;
            }
            else 
            {
                height[rp] >= rpmax ? (rpmax = height[rp]) : (ans += rpmax - height[rp]);
                rp--;
            }
        }
        return ans;
    }
};