算法基础

一、时间复杂度

用来评估算法运行效率的一个东西

print('Hello World') 

 O(1)

for i in range(n):

    print('Hello World')     

O(n)

for i in range(n):
    for j in range(n):
        print('Hello World')

O(n²)

for i in range(n):
    for j in range(n):
         for k in range(n):
             print('Hello World')

O(n*3)

 

  

时间复杂度是用来估计算法运行时间的一个式子（单位）。
一般来说，时间复杂度高的算法比复杂度低的算法慢。
常见的时间复杂度（按效率排序）
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
不常见的时间复杂度（看看就好）
O(n!) O(2n) O(nn) …

如何一眼判断时间复杂度？
循环减半的过程O(logn)
几次循环就是n的几次方的复杂度

 

递归

递归的两个特点：

调用自身

结束条件

练习：

 

 

def test(n):
    if n == 0:
        print("我的小鲤鱼", end='')
    else:
        print("抱着", end='')
        test(n-1)
        print("的我", end='')

test(5)

递归实例：汉诺塔问题

def move(n, a, buffer, c):
    if(n == 1):
        print(a,"->",c)
        return
    move(n-1, a, c, buffer)
    move(1, a, buffer, c)
    move(n-1, buffer, a, c)
move(3, "a", "b", "c")

列表查找

列表查找：

从列表中查找指定元素

输入：列表、待查找元素

输出：元素下标或未查找到元素

顺序查找

从列表第一个元素开始，顺序进行搜索，直到找到为止。

二分查找

从有序列表的候选区data[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。

 

递归版本的二分查找

def bin_search_rec(data_set, value, low, high):
    if low <= high:
        mid = (low + high) // 2
        if data_set[mid] == value:
            return mid
        elif data_set[mid] > value:
            return bin_search_rec(data_set, value, low, mid - 1)
        else:
            return bin_search_rec(data_set, value, mid + 1, high)
    else:
        return

LowB三人组

 冒泡排序

首先，列表每两个相邻的数，如果前边的比后边的大，那么交换这两个数

import time


def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2-t1))
        return result
    return wrapper

import random
from .timewrap import *

@cal_time
def bubble_sort(li):
    for i in range(len(li) - 1):
        # i 表示趟数
        # 第 i 趟时： 无序区：(0，len(li) - i)
        for j in range(0, len(li) - i - 1):
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]

#冒泡排序优化
#如果冒泡排序中执行一趟而没有交换，则列表已经是有序状态，可以直接结束算法。
@cal_time
def bubble_sort_2(li):
    for i in range(len(li) - 1):
        # i 表示趟数
        # 第 i 趟时： 无序区：(0，len(li) - i)
        change = False
        for j in range(0, len(li) - i - 1):
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]
                change = True
        if not change:
            return

li = list(range(10000))
# random.shuffle(li)
# print(li)
bubble_sort_2(li)
print(li)

'''
列表每两个相邻的数，如果前边的比后边的大，那么交换这两个数
时间复杂度O(n2)
'''

选择排序

一趟遍历记录最小的数，放到第一个位置； 再一趟遍历记录剩余列表中最小的数，继续放置； ……

import random
from .timewrap import *

@cal_time
def select_sort(li):
    for i in range(len(li) - 1):
        # i 表示趟数，也表示无序区开始的位置
        min_loc = i   # 最小数的位置
        for j in range(i + 1, len(li) - 1):
            if li[j] < li[min_loc]:
                min_loc = j
        li[i], li[min_loc] = li[min_loc], li[i]


li = list(range(10000))
random.shuffle(li)
print(li)
select_sort(li)
print(li)


'''
一趟遍历记录最小的数，放到第一个位置；
再一趟遍历记录剩余列表中最小的数，继续放置；
时间复杂度：O(n2)
'''

插入排序

列表被分为有序区和无序区两个部分。最初有序区只有一个元素。

每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空。

import random
from .timewrap import *

@cal_time
def insert_sort(li):
    for i in range(1, len(li)):
        # i 表示无序区第一个数
        tmp = li[i] # 摸到的牌
        j = i - 1 # j 指向有序区最后位置
        while li[j] > tmp and j >= 0:
            #循环终止条件： 1. li[j] <= tmp; 2. j == -1
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp


li = list(range(10000))
random.shuffle(li)
print(li)
insert_sort(li)
print(li)

'''
列表被分为有序区和无序区两个部分。最初有序区只有一个元素。
每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空。
O(n2)

'''

冒泡排序 插入排序 选择排序

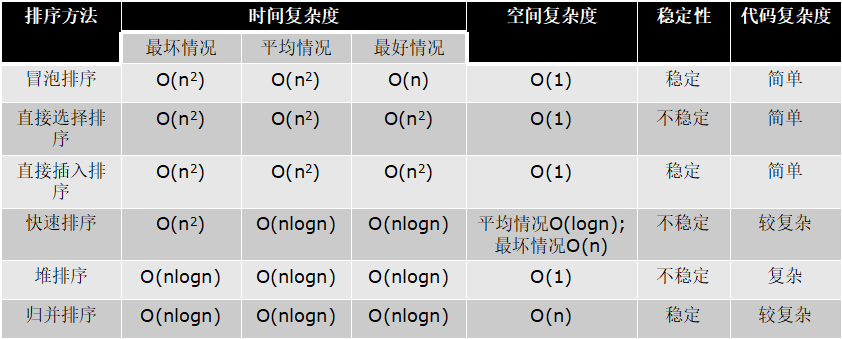
时间复杂度：O(n2)

空间复杂度：O(1)

NB三人组

快速排序

快速排序：快

快排思路：

取一个元素p（第一个元素），使元素p归位；

列表被p分成两部分，左边都比p小，右边都比p大；

递归完成排序。

import random
from .timewrap import *
import copy
import sys


sys.setrecursionlimit(100000)

def partition(li, left, right):
    # ri = random.randint(left, right)
    # li[left], li[ri] = li[ri], li[left]
    tmp = li[left]
    while left < right:
        while left < right and li[right] >= tmp:
            right -= 1
        li[left] = li[right]
        while left < right and li[left] <= tmp:
            left += 1
        li[right] = li[left]
    li[left] = tmp
    return left


def _quick_sort(li, left, right):
    if left < right:    # 至少有两个元素
        mid = partition(li, left, right)
        _quick_sort(li, left, mid-1)
        _quick_sort(li, mid+1, right)

@cal_time
def quick_sort(li):
    return _quick_sort(li, 0, len(li)-1)

@cal_time
def sys_sort(li):
    li.sort()

li = list(range(100000))
random.shuffle(li)


#sys_sort(li1)
quick_sort(li)


''''
快速排序：快
快排思路：
取一个元素p（第一个元素），使元素p归位；
列表被p分成两部分，左边都比p小，右边都比p大；
递归完成排序。
时间复杂度:一般为O(nlgn) 最坏情况为O(n2)
'''

效率

快速排序的时间复杂度

快速排序的问题

最坏情况

递归

堆排序

堆

大根堆：

一棵完全二叉树，满足任一节点都比其孩子节点大

小根堆：

一棵完全二叉树，满足任一节点都比其孩子节点小

堆排序过程

1.建立堆 得到

2.堆顶元素，为最大元素

3. 去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序。

4. 堆顶元素为第二大元素。

5.重复步骤3，直到堆变空。

from .timewrap import *
import random

def _sift(li, low, high):
    """
    :param li:
    :param low: 堆根节点的位置
    :param high: 堆最有一个节点的位置
    :return:
    """
    i = low  # 父亲的位置
    j = 2 * i + 1  # 孩子的位置
    tmp = li[low]  # 原省长
    while j <= high:
        if j + 1 <= high and li[j + 1] > li[j]:  # 如果右孩子存在并且右孩子更大
            j += 1
        if tmp < li[j]:  # 如果原省长比孩子小
            li[i] = li[j]  # 把孩子向上移动一层
            i = j
            j = 2 * i + 1
        else:
            li[i] = tmp  # 省长放到对应的位置上(干部)
            break
    else:
        li[i] = tmp  # 省长放到对应的位置上(村民/叶子节点)


def sift(li, low, high):
    """
    :param li:
    :param low: 堆根节点的位置
    :param high: 堆最有一个节点的位置
    :return:
    """
    i = low         # 父亲的位置
    j = 2 * i + 1   # 孩子的位置
    tmp = li[low]   # 原省长
    while j <= high:
        if j + 1 <= high and li[j+1] > li[j]: # 如果右孩子存在并且右孩子更大
            j += 1
        if tmp < li[j]: # 如果原省长比孩子小
            li[i] = li[j]  # 把孩子向上移动一层
            i = j
            j = 2 * i + 1
        else:
            break
    li[i] = tmp


@cal_time
def heap_sort(li):
    n = len(li)
    # 1. 建堆
    for i in range(n//2-1, -1, -1):
        sift(li, i, n-1)
    # 2. 挨个出数
    for j in range(n-1, -1, -1):    # j表示堆最后一个元素的位置
        li[0], li[j] = li[j], li[0]
        # 堆的大小少了一个元素 （j-1）
        sift(li, 0, j-1)


li = list(range(10000))
random.shuffle(li)
heap_sort(li)
print(li)

# li=[2,9,7,8,5,0,1,6,4,3]
# sift(li, 0, len(li)-1)
# print(li)

''''
建立堆
得到堆顶元素，为最大元素
去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序。
堆顶元素为第二大元素。
重复步骤3，直到堆变空。

时间复杂度O(nlgn)
'''

堆排序——内置模块

优先队列：

一些元素的集合，POP操作每次执行都会从优先队列中弹出最大（或最小）的元素。

堆——优先队列

Python内置模块——heapq h

heapify(x)

heappush(heap, item)

heappop(heap)

利用heapq模块实现堆排序

import heapq, random

li = [5,8,7,6,1,4,9,3,2]

heapq.heapify(li)
print(heapq.heappop(li))
print(heapq.heappop(li))

def heap_sort(li):
    heapq.heapify(li)
    n = len(li)
    new_li = []
    for i in range(n):
        new_li.append(heapq.heappop(li))
    return new_li

li = list(range(10000))
random.shuffle(li)
# li = heap_sort(li)
# print(li)

print(heapq.nlargest(100, li))

归并排序

import random
from timewrap import *
import copy
import sys


def merge(li, low, mid, high):
    i = low
    j = mid + 1
    ltmp = []
    while i <= mid and j <= high:
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1
    while i <= mid:
        ltmp.append(li[i])
        i += 1
    while j <= high:
        ltmp.append(li[j])
        j += 1
    li[low:high+1] = ltmp


def _merge_sort(li, low, high):
    if low < high:  # 至少两个元素
        mid = (low + high) // 2
        _merge_sort(li, low, mid)
        _merge_sort(li, mid+1, high)
        merge(li, low, mid, high)
        print(li[low:high+1])


def merge_sort(li):
    return _merge_sort(li, 0, len(li)-1)


li = list(range(16))
random.shuffle(li)
print(li)
merge_sort(li)

print(li)

nb三人组三种排序算法的时间复杂度都是O(nlogn)

一般情况下，就运行时间而言： 快速排序 < 归并排序 < 堆排序

三种排序算法的缺点：

快速排序：极端情况下排序效率低

归并排序：需要额外的内存开销

堆排序：在快的排序算法中相对较慢

 其他排序

希尔排序

希尔排序是一种分组插入排序算法。

首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1，在各组内进行直接插入排序；

取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内进行直接插入排序。

希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序。

def insert_sort(li):
    for i in range(1, len(li)):
        # i 表示无序区第一个数
        tmp = li[i] # 摸到的牌
        j = i - 1 # j 指向有序区最后位置
        while li[j] > tmp and j >= 0:
            #循环终止条件： 1. li[j] <= tmp; 2. j == -1
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp

def shell_sort(li):
    d = len(li) // 2
    while d > 0:
        for i in range(d, len(li)):
            tmp = li[i]
            j = i - d
            while li[j] > tmp and j >= 0:
                li[j+d] = li[j]
                j -= d
            li[j+d] = tmp
        d = d >> 1

计数排序

# 0 0 1 1 2 4 3 3 1 4 5 5
import random
import copy
from timewrap import *

@cal_time
def count_sort(li, max_num = 100):
    count = [0 for i in range(max_num+1)]
    for num in li:
        count[num]+=1
    li.clear()
    for i, val in enumerate(count):
        for _ in range(val):
            li.append(i)

@cal_time
def sys_sort(li):
    li.sort()

li = [random.randint(0,100) for i in range(100000)]
li1 = copy.deepcopy(li)
count_sort(li)
sys_sort(li1)

基数排序

import random
from .timewrap import *

def list_to_buckets(li, iteration):
    """
    :param li: 列表
    :param iteration: 装桶是第几次迭代
    :return:
    """
    buckets = [[] for _ in range(10)]
    for num in li:
        digit = (num // (10 ** iteration)) % 10
        buckets[digit].append(num)
    return buckets

def buckets_to_list(buckets):
    return [num for bucket in buckets for num in bucket]
    # li = []
    # for bucket in buckets:
    #     for num in bucket:
    #         li.append(num)

@cal_time
def radix_sort(li):
    maxval = max(li) # 10000
    it = 0
    while 10 ** it <= maxval:
        li = buckets_to_list(list_to_buckets(li, it))
        it += 1
    return li

li = [random.randint(0,1000) for _ in range(100000)]
radix_sort(li)

给定一个升序列表和一个整数，返回该整数在列表中的下标范围

def twoSum(nums, target):
    """
    :type nums: List[int]
    :type target: int
    :rtype: List[int]
    """
    for i in range(len(nums)):
        for j in range(i+1,len(nums)):
            if nums[i]+nums[j] == target:
                return [i,j]

def twoSum(nums, target):

    d = {}
    for i in range(len(nums)):
        if target - nums[i] in d:
                return i, d[target-nums[i]]
        else:
            d[nums[i]] = i

找出第k大的数

def partition(array, left, right):
    well = left
    for i in range(left, right):
        if array[i] > array[right]:
            array[i], array[well] = array[well], array[i]
            well += 1
    array[well], array[right] = array[right], array[well]
    return well

def findk(l,low,high,k):
    if low<=high:
        mid=partition(l, low, high)
        if mid==len(l)-k:
            res=l[mid]
            return res
        elif mid>len(l)-k:
            return findk(l,low,mid-1,k)
        else:
            return findk(l,mid+1,high,k)



l=[1,23,4,5,64,68,12,45,666,999,69]
res=findk(l,0,len(l)-1,6)
print("res:",res,l)

def kp(data, left, right):
    tem = data[left]
    while left < right:
        while left < right and data[right] >= tem:
            right -= 1
        data[left] = data[right]
        while left < right and data[left] <= tem:
            left += 1
        data[right] = data[left]

    data[right] = tem
    return left

def qk(data, left, right):
    if left <right:
        mid = kp(data, left,right)
        qk(data,left, mid-1)
        qk(data,mid+1, right)




k=5
data = [1, 23, 4, 5, 64, 68, 12, 45, 666, 999, 69]
qk(data, 0, len(data)-1)
data.reverse()
print(data)
print(data[len(data) -1-k-1])