数据结构

一、数据结构分类

数组、串、栈、队列、链表、树、散列、堆、图

 

二、数组

顺序储存结构

 

三、链表

单链表、静态链表、循环链表、双向链表

单链表操作

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
    ListNode resultHead = new ListNode(0);
    ListNode p = l1, q = l2, curr = resultHead;
    int carry = 0;
    while(p != null || q != null) {
        int a = p != null ? p.val : 0;
        int b = q != null ? q.val : 0;
        int sum = a + b + carry;
        carry = sum / 10;
        curr.next = new ListNode(sum % 10);
        curr = curr.next;
        if(p != null) p = p.next;
        if(q != null) q = q.next;
    }
    if(carry != 0) {
        curr.next = new ListNode(1);
    }
    return resultHead.next;
}

用链表模拟两数相加

 

四、串 

KMP（字符串匹配）

 

五、栈

顺序栈、链栈

 

六、队列

顺序队列、循环队列、链队列

 

七、树

1、二叉树

 

 

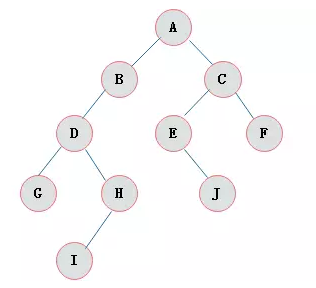
1、每个结点最多有两颗子树

2、左子树和右子树是有顺序的，次序不能任意颠倒

3、即使树中某结点只有一棵子树，也要区分它是左子树还是右子树

 

2、满二叉树

 

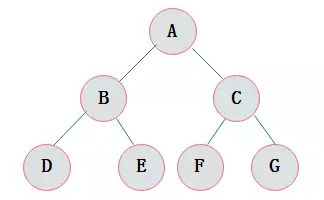
1、叶子只能出现在最下一层。出现在其它层就不可能达成平衡

2、非叶子结点的度一定是2

3、在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多

 

3、完全二叉树

 

1、叶子结点只能出现在最下层和次下层

2、最下层的叶子结点集中在树的左部

3、倒数第二层若存在叶子结点，一定在右部连续位置

4、如果结点度为1，则该结点只有左孩子，即没有右子树

5、同样结点数目的二叉树，完全二叉树深度最小

 

4、二叉搜索树

 

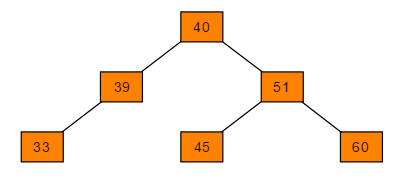
1、若左子树不空，则左子树上所有节点的值均小于它的根节点的值

2、若右子树不空，则右子树上所有节点的值均大于它的根节点的值

3、左、右子树也分别为二叉搜索树

 

5、平衡二叉树、AVL树

 

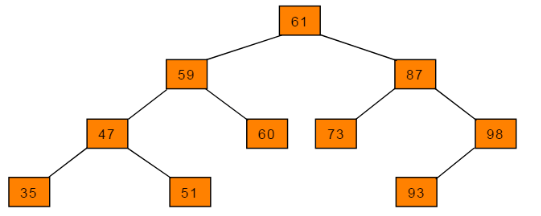
1、必须是二叉查找树

2、每个节点的左子树和右子树的高度差至多为1

 

6、红黑树

 

1、节点是要么红色或要么是黑色
2、根一定是黑色节点
3、每个叶子节点都带有两个空的黑色节点（称之为NIL节点，它又被称为黑哨兵）
4、每个红色节点的两个子节点都是黑色（或者说从每个叶子到根的所有路径上不能有两个连续的红色节点）
5、从任一节点到它所能到达得叶子节点的所有简单路径都包含相同数目的黑色节点

 

7、霍夫曼树、最优二叉树

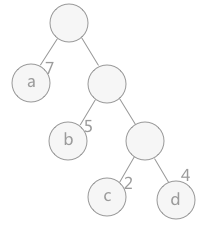
1、每个叶子结点且都有各自的权值

2、构建的这棵树的带权路径长度最小

 

8、B树

 

 

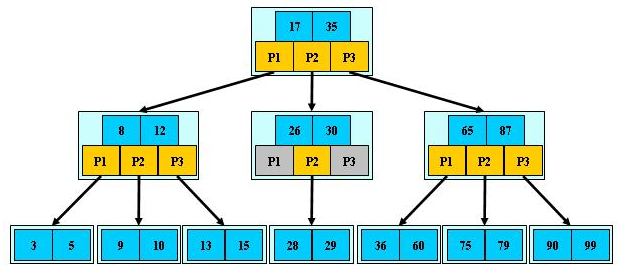
1、每个结点最多有m-1个关键字
2、根结点最少可以只有1个关键字
3、非根结点至少有Math.ceil(m/2)-1个关键字。Math.ceil(m/2)含义是向上取整。例如Math.ceil(4.5) = 5
4、每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它
5、所有叶子结点都位于同一层，或者说根结点到每个叶子结点的长度都相同

 

9、B+树

 

 

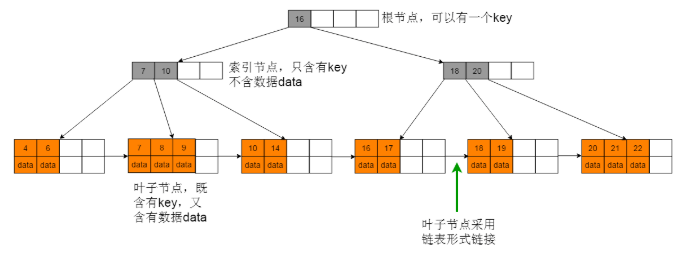
1、B+树与B树最大的不同是内部结点不保存数据，只用于索引，所有数据（或者说记录）都保存在叶子结点中

2、每个叶子结点都存有相邻叶子结点的指针，叶子结点本身依关键字的大小自小而大顺序链接

 

八、堆

同完全二叉树

 

九、散列

散列冲突、拉链法

 

十、图

先略