MPC特点原理以及各项参数的选择--引用别人的博客网址
参见:MATLAB techtalk 中关于MPC的讲解视频:
https://www.mathworks.com/videos/series/understanding-model-predictive-control.html
或者: Understanding Model Predictive Control(B站 )
下面是转载别人参照视频所作的笔记记录:https://zhkmxx9302013.github.io/post/10696.html
参见网址:https://zhuanlan.zhihu.com/p/139833089
https://blog.csdn.net/u013414501/article/details/82657583
https://blog.csdn.net/u013414501/article/details/51772672
MPC的三大要素:
预测模型——对未来一段时间内的输出进行预测;
滚动优化——滚动进行有限时域在线优化(最优控制);
反馈校正——通过预测误差反馈,修正预测模型,提高预测精度。

Mo(measured output): 当前可测量的输出信号
Ref(Reference signa): 参考信号
Md(optional measured disturbance signa): 可选的测量干扰信号
Mv(optimal manipulated variables ):最优操纵变量
MPC一般通过求解一个二次规划来计算最优操纵变量
MPC作用机理为:
在每一个采用时刻,根据获得的当前测量信息,在线求解一个有限时间开环优化问题,并将得到的控制序列的第一个元素作用于被控对象。在下一个采样时刻,重复上述过程:用新的测量值作为此时预测系统未来动态的初始条件,刷新优化问题并重新求解 。即MPC算法包括三个步骤:
(1)预测系统未来动态;
(2)(数值)求解开环优化问题;
(3)将优化解的第一个元素(或者说第一部分)作用于系统
这三步是在每个采样时刻重复进行的,且无论采用什么样的模型,每个采样时刻得到的测量值都作为当前时刻预测系统未来动态的初始条件
在线求解开环优化问题获得开环优化序列是MPC和传统控制方法的主要区别,因为后者通常是离线求解一个反馈控制律,并将得到的反馈控制律一直作用于系统。
在这里给出两点说明:
1.MPC是一个反馈控制策略,但是之前不是说将得到的控制序列中的第一个元素作用于被控对象,求解开环问题。那么哪来的反馈呢?
实际上在下一个采样周期,下一时刻的测量值又被使用上了,用下一时刻的测量值求解下一时刻的控制值。故这是一个反馈控制策略
2.传统的控制方法为什么被称为离线控制?
设计变阻器应有的级数来达到控制并励直流电动机启动的例子,那么如何看的出来是离线控制呢?其实很简单,在起始的时候就已经把每级电阻值就给定出来了,
但是实际上是否能如理论计算的这样呢?比如我电压突然受到了扰动了怎么办?那么这个计算的每级电阻值肯定不对了啦,但是传统的控制方法对此确是无能为力的,因为每级启动电阻在最早的时候已经计算好了的。
MPC的基本特点
不管是何种算法,他们的基本特点都是:基于模型的预测、滚动优化和前馈-反馈的控制结构。
1.基于模型的预测
在MPC算法中,需要一个描述对象动态行为的模型,这个模型的作用是预测系统未来的动态。即能够根据系统k时刻的状态和k时刻的控制输入,
预测到k+1时刻的输出。在这里k时刻的输入正是用来控制系统k+1时间的输出,使其最大限度的接近k+1时刻的期望值。故我们强调的是该模型的预测作用,而不是模型的形式。
在这里我重点讲解一下状态空间模型。那么什么是状态?输出是不是也是状态的一种?对的,输出也是一种状态,只不过我们赋予了这个状态特殊的意义。
举个例子来说,舞龙,假设是只能通过龙尾的人A指挥前面一个人B动作,然后B指挥他前面的一个人C动作….依次如此,达到控制龙头的人F叼住绣球的动作。
如果只关注龙头的人(输出)和龙尾的人(输入),而忽略龙身子的动态,那就是所谓的输入—输出系统。经典控制理论就是建立在输入—输出系统的基础上面的。
但是我如果不管要管龙尾和龙头的人,我连龙身子上面的人也要要求在固定的位置,那么这就是状态空间的概念,即我对系统中的每一个状态都要控制到。
龙头位置的人也是一个状态,故输出本身就是一个状态,或者说是状态的一个组合。
2.滚动优化
因为外部干扰和模型失配的影响,系统的预测输出和实际输出存在着偏差,如果测量值能测到这个偏差,那么在下一时刻能根据这个测量到偏差的测量值在线求解下一时刻的控制输入,
即优化掉了这个偏差值。若将求解的控制输出的全部序列作用于系统,那么k+1时刻的测量值不能影响控制动作,也就是说测量值所包括的外部干扰或模型误差信息得不到有效利用。
故我们将每个采样时刻的优化解的第一个分量作用于系统,在下一个采用时刻,根据新得到的测量值为初始条件重新预测系统的未来输出并求解优化解,继续讲这个时刻的优化解
的第一个分量作用于系统,这样重复至无穷。故预测控制不是采用一个不变的全局优化目标,而是采用时间向前滚动式的有限时域优化策略。
这也就是意味着优化过程不是一次离线进行,而是反复在线进行的。
下面是转载别人参照视频所作的笔记记录:https://zhkmxx9302013.github.io/post/10696.html
一、什么是MPC模型预测控制
MPC(Model Predict Control)是一种反馈控制(feedback control)算法, 使用模型来预测过程的未来输出。
举例:
[场景] 车道保持
[已知模型] 车辆模型,比如速度控制, 转向控制对应的偏航量
[预测] 根据已知模型和所选的控制策略(action),进行轨迹预测
[优化] 通过优化控制策略,来尽可能的拟合预测的轨迹。
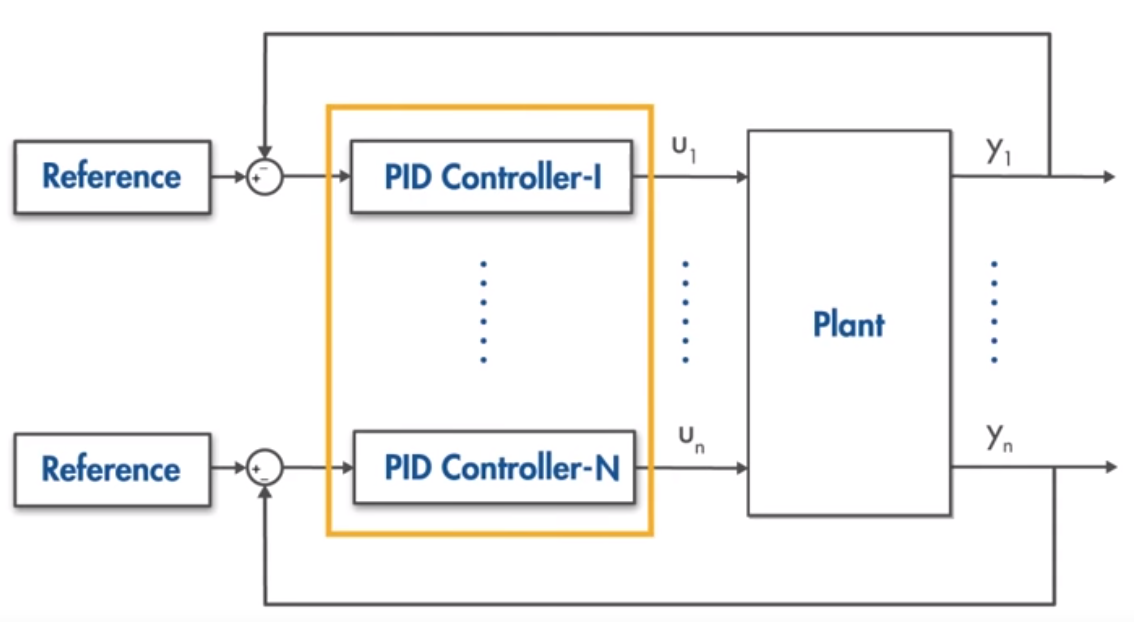
如下图所示为一个MIMO系统u1,u2输入与y1,y2输出相互影响。如果使用PID控制的话,每一个子系统单独设计一个PID控制器,
两个相互影响的子系统没有任何的交联,使得系统难以设计,如果像图二一样设计一个较大的系统,则参数较多难以实现,
而使用MPC控制器的话可以较好的解决两种问题,综合相互间的影响来设计参数。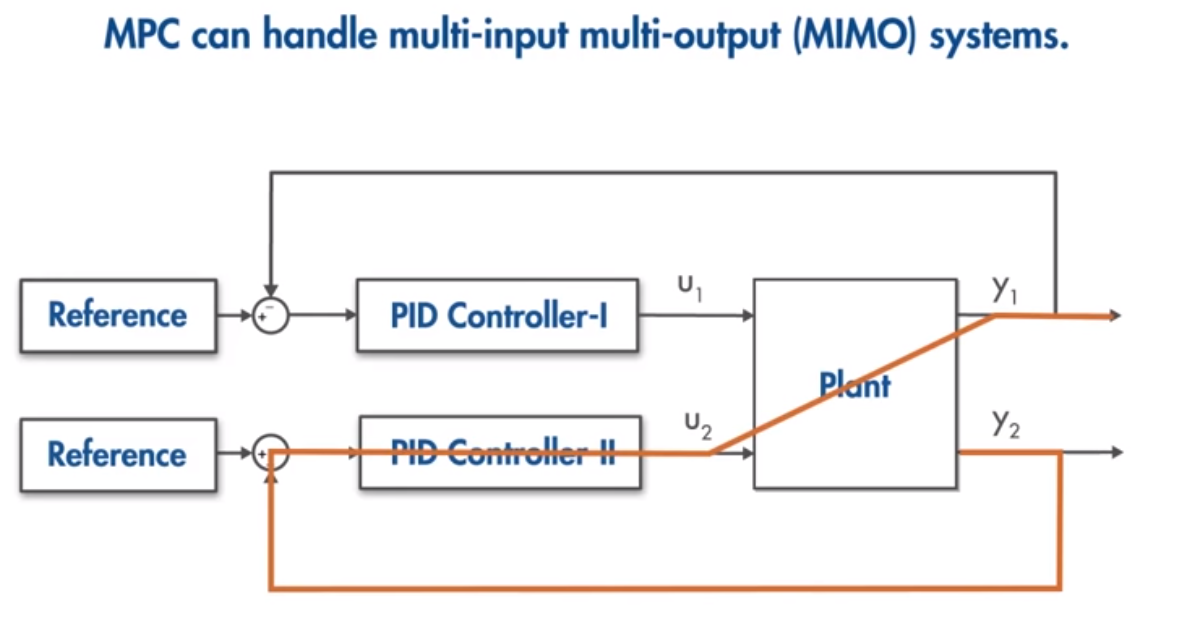
MPC控制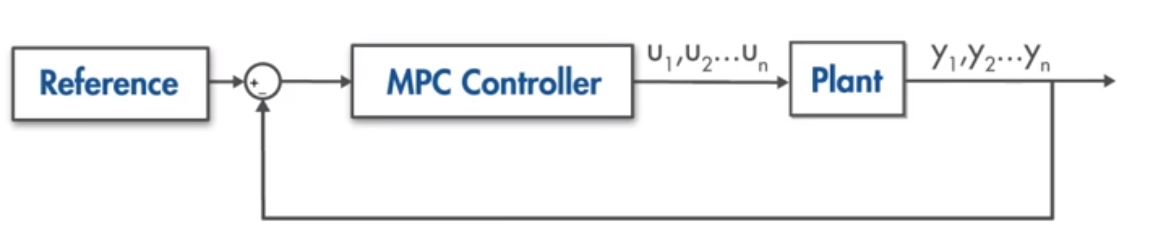
此外MPC控制还可以方便的支持各种约束条件,具备一定的预测能力(有点像前馈feedforward控制)。
二、MPC的特点
综合上述,总结一下MPC的特点:
- 支持MIMO系统,便于构建输入输出间的相互影响参数
- 支持方便添加约束条件
- 具有预测能力、
- 需要较好的处理器和较大的内存,因为需要大量的在线优化,存储大量的变量
-
MPC相对于LQR控制而言,MPC可以考虑空间状态变量的各种约束,而LQR,PID等控制只能够考虑输入输出变量的各种约束。
MPC可应用于线性和非线性系统。

三、MPC参数选择
选择一个好的参数不仅影响MPC控制的性能,而且还会影响到MPC每一个timestep内进行在线优化的计算复杂度。
这里将会给出关于控制器采样周期、预测及控制范围(prediction and control)、约束及权重。
采样周期的选择
采样周期过大,则系统反应过慢导致难以及时进行修正控制,而采样周期过小,则会导致系统产生大量的在线优化计算,给系统带来较大的开销。
因而建议采样周期设计采用开环响应时间(10~90%上升时间)的十分之一或二十分之一:
预测范围(prediction horizon)的选择
预测范围指的是一次优化后预测未来输出的时间步的个数。建议范围:在开环响应时间内采样20-30个样本的范围
控制范围(control horizon)的选择
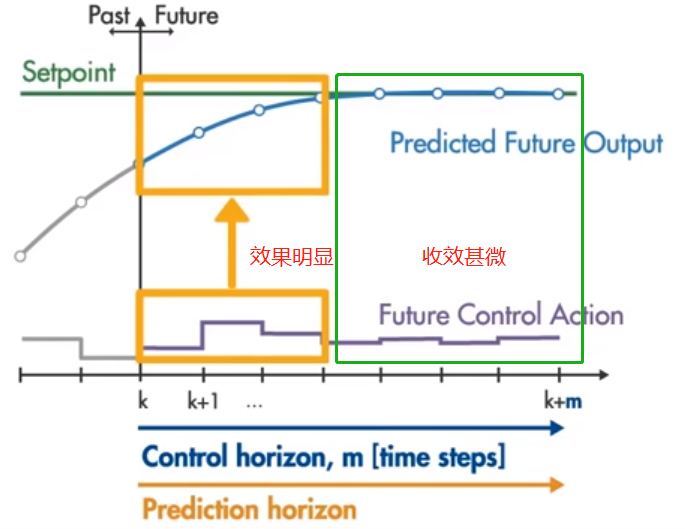
如下图 [k, k+m]范围为控制范围,之后的红色部分称为 held constant,其中控制范围是要通过优化器来进行优化的参数动作。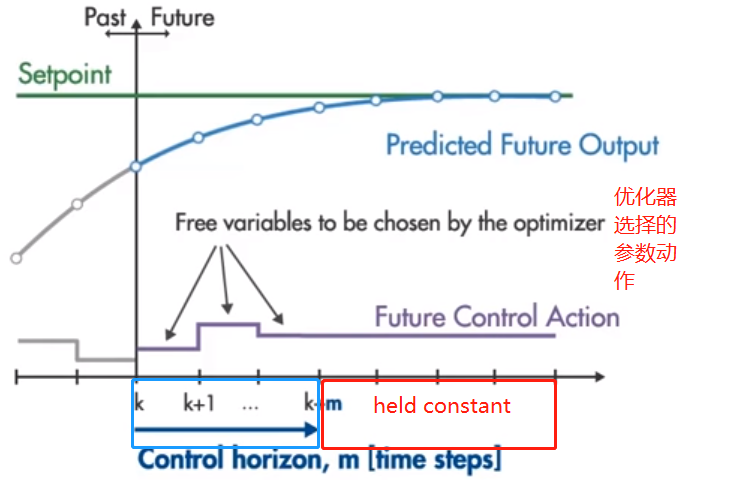
过小的控制范围,可能无法做到较好的控制,而较大的控制范围,比如与预测范围相等,则会导致只有前一部分的控制范围才会有较好的效果,
建议控制范围应该在预测范围的10~20%之间,最小值为2~3个timestep时间步
约束
对于约束,一般分为Hard约束和Soft约束,Hard约束是不可违背必须遵守的,在控制系统中,输入输出都可能会有约束限制,
但是在设计时不建议将输入输出都给予Hard约束,因为这两部的约束有可能是有重叠的,导致优化器会产生不可行解。
建议输出采用较小容忍度的Soft约束,而输入的话建议输入和输入参数变化率二者之间不要同时为Hard约束,可以一个Hard一个Soft。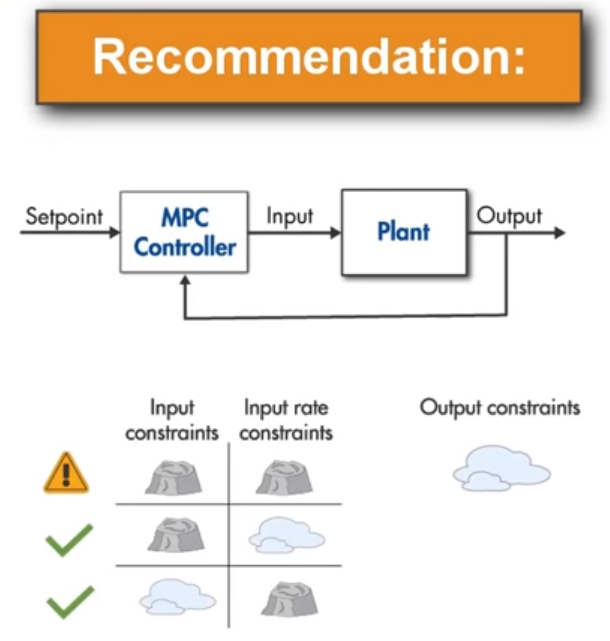
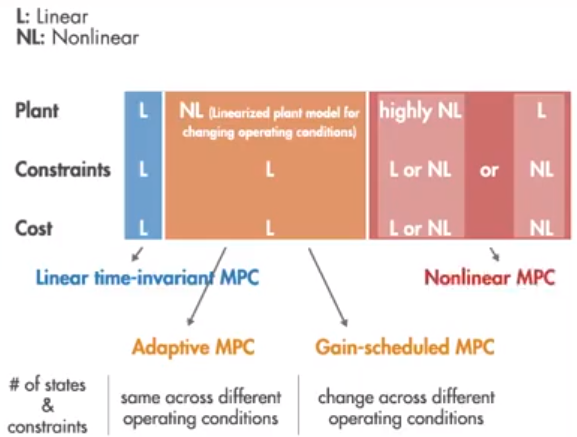
四、Linear MPC (Adaptive MPC 与 Gain-Scheduled MPC)
Linear MPC适用于: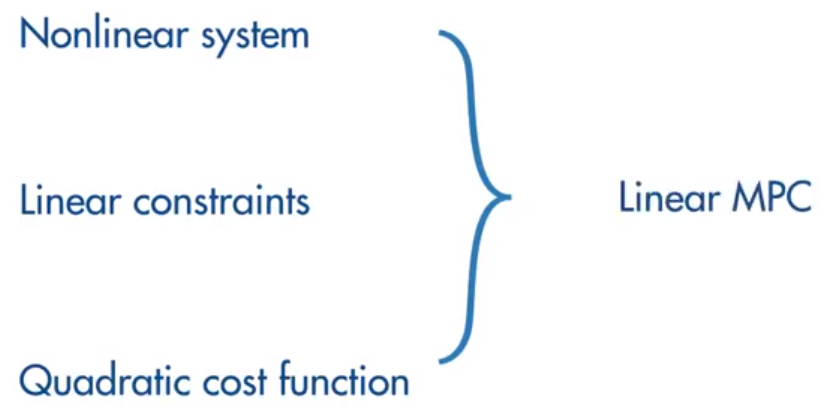
对于非线性系统而言,需要在不同的operating point处进行线性化处理如下图。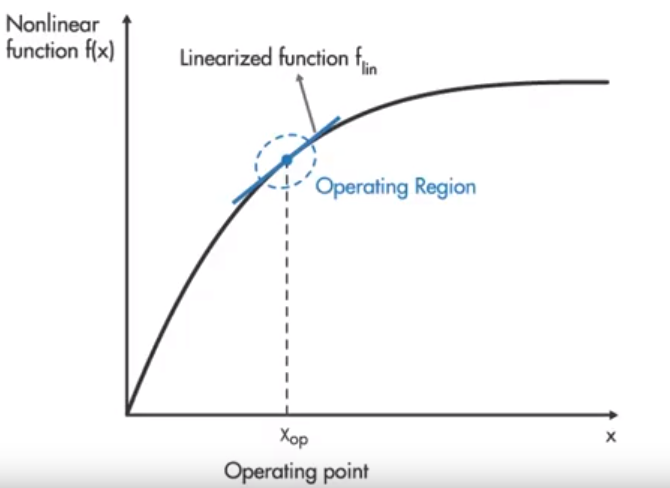
Adaptive MPC
在 Adaptive MPC中,当operating condition发生变化的时候,需要进行一次近似线性化计算,在每个时间步中,
使用其近似线性模型来更新内部的平台模型(plant model,比如飞控模型,自行车模型等)。
在 Adaptive MPC中,在不同的operating point条件下,其优化问题的结构保持不变,即状态数量,约束数量不会随着operating condition而改变。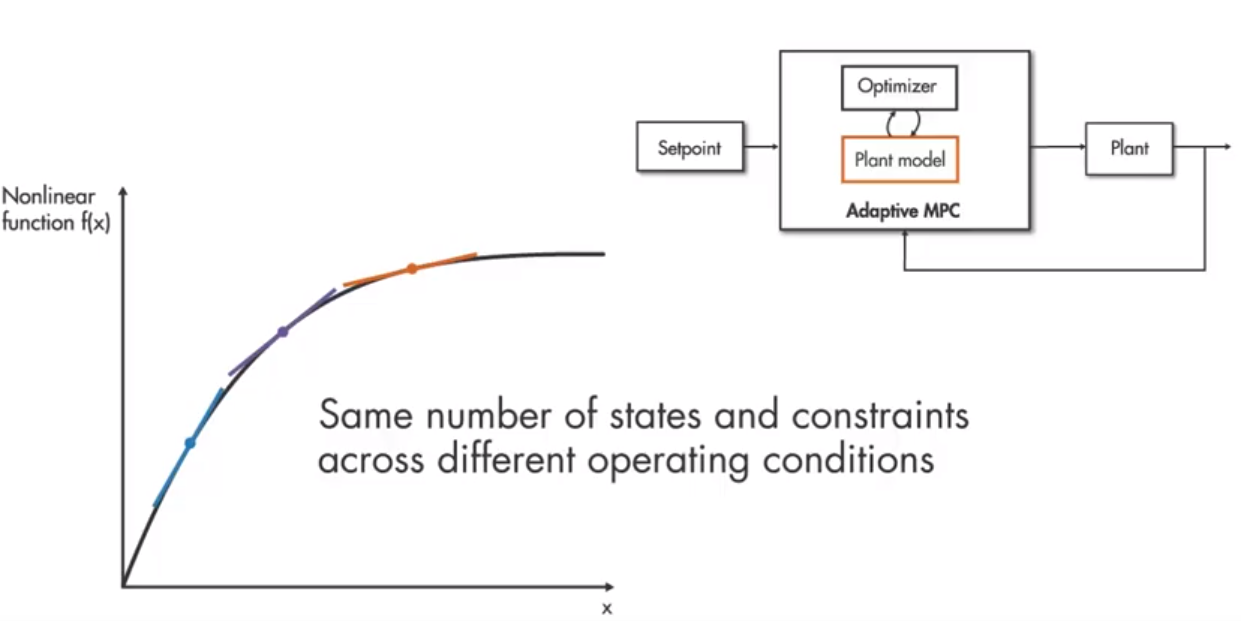
Gain-Scheduled MPC
在 Gain-Scheduled MPC中,在不同的operating point条件下,其优化问题的结构会发生变化,需要为每一个operating point构建一个MPC控制器,且相互之间独立,其状态数量约束数量也可能不同。
在 Gain-Scheduled MPC模式下,需要设计调度算法来切换不同的MPC模型。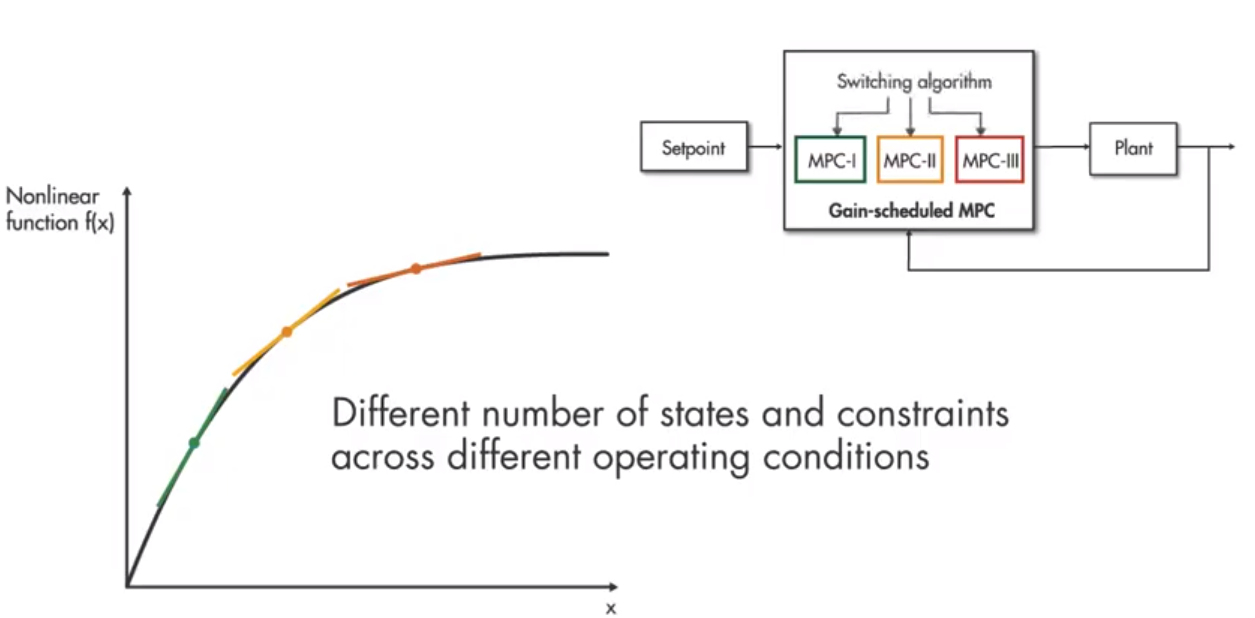
二者选型
[Adaptive MPC] 当能够构建平台(如飞行器,自动车等)的runtime线性模型,且在不同的operating point下优化问题的结构不变。
[Gain-Scheduled MPC] 当能够构建平台(如飞行器,自动车等)的runtime线性模型,且在不同的operating point下优化问题的结构发生变化。
五、Non-Linear MPC (Adaptive MPC 与 Gain-Scheduled MPC)
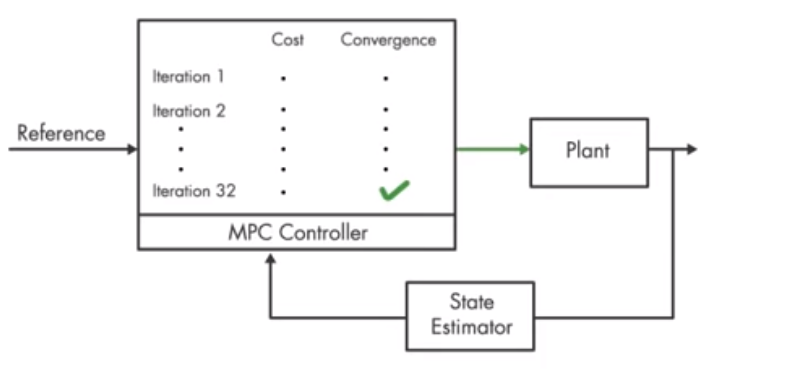
Non-Linear MPC适用于(相对强大,能够提供更准确的预测能力,与决策支持,但是非线性优化的计算开销较大)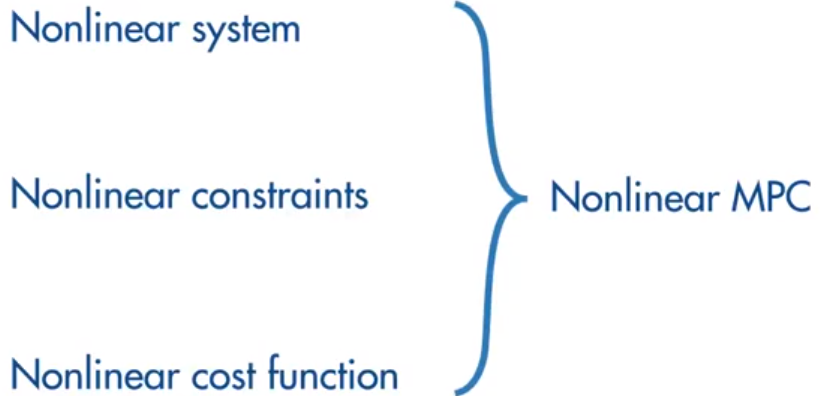





 浙公网安备 33010602011771号
浙公网安备 33010602011771号