凸包算法详解
Graham扫描法
时间复杂度:O(n㏒n)
思路:Graham扫描的思想是先找到凸包上的一个点,然后从那个点开始按逆时针方向逐个找凸包上的点,实际上就是进行极角排序,然后对其查询使用。 
步骤:
- 把所有点放在二维坐标系中,则纵坐标最小的点一定是凸包上的点,如图中的P0。
- 把所有点的坐标平移一下,使 P0 作为原点,如上图。
- 计算各个点相对于 P0 的幅角 α ,按从小到大的顺序对各个点排序。当 α 相同时,距离 P0 比较近的排在前面。例如上图得到的结果为 P1,P2,P3,P4,P5,P6,P7,P8。我们由几何知识可以知道,结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
(以上是准备步骤,以下开始求凸包)
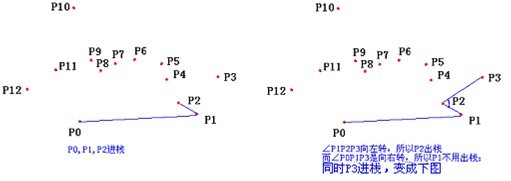
以上,我们已经知道了凸包上的第一个点 P0 和第二个点 P1,我们把它们放在栈里面。现在从步骤3求得的那个结果里,把 P1 后面的那个点拿出来做当前点,即 P2 。接下来开始找第三个点: - 连接P0和栈顶的那个点,得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5;如果在直线上,或者在直线的左边就执行步骤6。
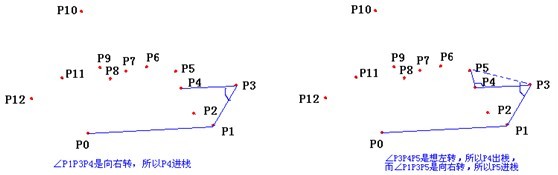
- 如果在右边,则栈顶的那个元素不是凸包上的点,把栈顶元素出栈。执行步骤4。
- 当前点是凸包上的点,把它压入栈,执行步骤7。
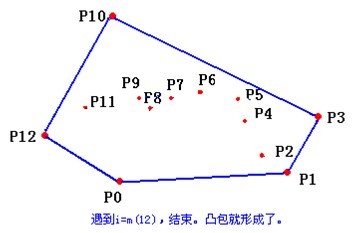
- 检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点,返回步骤4。
最后,栈中的元素就是凸包上的点了。
以下为用Graham扫描法动态求解的过程:
下面静态求解过程



1 #include<iostream> 2 #include<string.h> 3 #include<algorithm> 4 #include<cstdio> 5 #include<cmath> 6 using namespace std; 7 const int maxn=105; 8 const double PI=acos(-1.0); 9 struct node{int x,y;}; 10 node vex[maxn];//存入所有坐标点 11 node stackk[maxn];//凸包中所有的点 12 bool cmp1(node a,node b){//按点的坐标排序 13 if(a.y==b.y)return a.x<b.x;//如果纵坐标相同,则按横坐标升序排 14 else return a.y<b.y;//否则按纵坐标升序排 15 } 16 bool cmp2(node a,node b){//以基点为坐标原点,极角按升序排,这里可用atan2函数或者叉积来进行极角排序,但是用atan2函数来排序效率高时间快,不过精度比叉积低 17 double A=atan2(a.y-stackk[0].y,a.x-stackk[0].x);//返回的是原点至点(x,y)的方位角,即与x轴的夹角 18 double B=atan2(b.y-stackk[0].y,b.x-stackk[0].x); 19 if(A!=B)return A<B;//逆时针方向为正值,极角小的排在前面 20 else return a.x<b.x;//如果极角相同,则横坐标在前面的靠前排列 21 } 22 int cross(node p0,node p1,node p2){//计算两个向量a、b(a=(x1,y1),b=(x2,y2))的叉积公式:a×b=x1y2-x2y1 ===> p0p1=(x1-x0,y1-y0),p0p2=(x2-x0,y2-y0) 23 return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y); 24 } 25 double dis(node a,node b){//计算两点之间的距离 26 return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y)); 27 } 28 int main(){ 29 int t; 30 while(~scanf("%d",&t)&&t){ 31 for(int i=0;i<t;++i)//输入t个点 32 scanf("%d%d",&vex[i].x,&vex[i].y); 33 if(t==1)printf("%.2f\n",0.00);//如果只有一个点,则周长为0.00 34 else if(t==2)printf("%.2f\n",dis(vex[0],vex[1]));//如果只有两个点,则周长为两个点的距离 35 else{ 36 memset(stackk,0,sizeof(stackk));//清0 37 sort(vex,vex+t,cmp1);//先按坐标点的位置进行排序 38 stackk[0]=vex[0];//取出基点 39 sort(vex+1,vex+t,cmp2);//将剩下的坐标点按极角进行排序,以基点为坐标原点 40 stackk[1]=vex[1];//将凸包中的第二个点存入凸集中 41 int top=1;//当前凸包中拥有点的个数为top+1 42 for(int i=2;i<t;++i){//不断地找外围的坐标点 43 while(top>0&&cross(stackk[top-1],stackk[top],vex[i])<=0)top--;//如果叉积为负数或0(0表示两向量共线),则弹出栈顶元素 44 //虽然第2个凸点显然是最外围的一点,但加上top>0保证了栈中至少有2个凸点 45 stackk[++top]=vex[i]; 46 } 47 double s=0; 48 for(int i=1;i<=top;++i)//计算凸包的周长 49 s+=dis(stackk[i-1],stackk[i]); 50 s+=dis(stackk[top],vex[0]);//最后一个点和第一个点之间的距离 51 printf("%.2f\n",s); 52 /* 53 int s=0;//计算凸包的面积 54 for(int i=1;i<=top;i++) 55 s+=cross(st[i-1],st[i],e[0])/2; 56 */ 57 } 58 } 59 return 0; 60 }




