KMP算法详解
让我们来看一组例子:
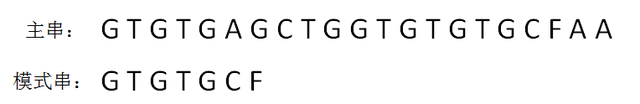
模式串和主串的第一个等长子串比较,发现前5个字符都是匹配的,第6个字符不匹配,是一个“坏字符”:

我们可以发现,在前缀“GTGTG”当中,后三个字符“GTG”和前三位字符“GTG”是相同的:

在下一轮的比较时,只有把这两个相同的片段对齐,才有可能出现匹配。这两个字符串片段,分别叫做最长可匹配后缀子串和最长可匹配前缀子串。
第二轮,我们直接把模式串向后移动两位,让两个“GTG”对齐,继续从刚才主串的坏字符A开始进行比较:
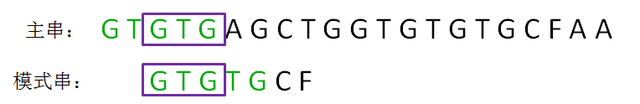
按照第一轮的思路,我们来重新确定最长可匹配后缀子串和最长可匹配前缀子串:

我们再次把模式串向后移动两位,让两个“G”对齐,继续从刚才主串的坏字符A开始进行比较:
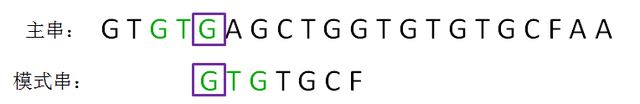
那么,我们如何找到一个字符串最长可匹配后缀子串和最长可匹配前缀子串,难道在每一轮都重新遍历吗?
我们可以事先缓存到一个集合中,用到的时候再去集合中里面取 即next 数组;
**next 数组:
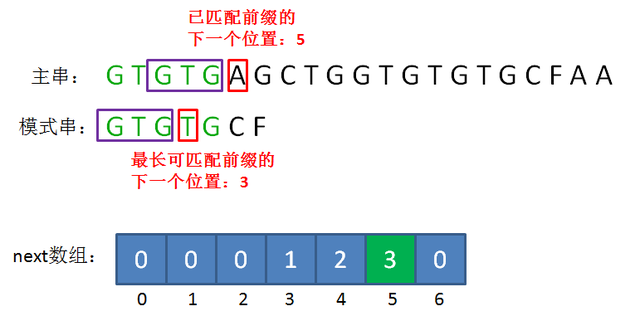
这是一个一维整型数组,数组的下标代表了“已匹配前缀的下一个位置”,元素的值则是“最长可匹配前缀子串的下一个位置”。
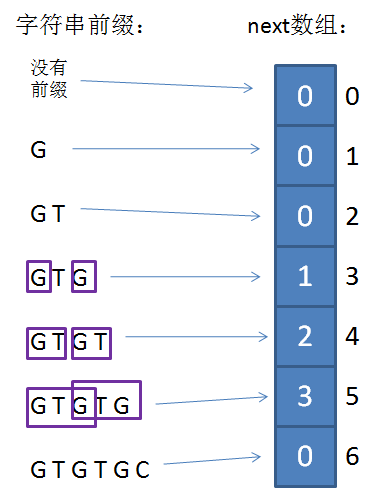
当模式串的第一个字符就和主串不匹配时,并不存在已匹配前缀子串,更不存在最长可匹配前缀子串。这种情况对应的next数组下标是0,next[0]的元素值也是0。
如果已匹配前缀是G、GT、GTGTGC,并不存在最长可匹配前缀子串,所以对应的next数组元素值(next[1],next[2],next[6])同样是0。
GTG的最长可匹配前缀是G,对应数组中的next[3],元素值是1。
以此类推,
GTGT 对应 next[4],元素值是2。
GTGTG 对应 next[5],元素值是3。
有了next数组,我们就可以通过已匹配前缀的下一个位置(坏字符位置),快速寻找到最长可匹配前缀的下一个位置,然后把这两个位置对齐。
比如下面的场景,我们通过坏字符下标5,可以找到next[5]=3,即最长可匹配前缀的下一个位置:
如何事先生成这个next数组呢?
我们可以采用类似“动态规划”的方法。首先next[0]和next[1]的值肯定是0,因为这时候不存在前缀子串;从next[2]开始,next数组的每一个元素都可以由上一个元素推导而来。
已知next[i]的值,如何推导出next[i+1]呢?让我们来演示一下上述next数组的填充过程:

如图所示,我们设置两个变量i和j,其中i表示“已匹配前缀的下一个位置”,也就是待填充的数组下标,j表示“最长可匹配前缀子串的下一个位置”,也就是待填充的数组元素值。
当已匹配前缀不存在的时候,最长可匹配前缀子串当然也不存在,所以i=0,j=0,此时next[0] = 0。
接下来,我们让已匹配前缀子串的长度加1:
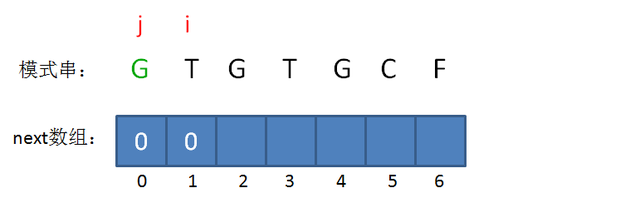
此时的已匹配前缀是G,由于只有一个字符,同样不存在最长可匹配前缀子串,所以i=1,j=0,next[1] = 0。
我们让已匹配前缀子串的长度继续加1:

此时的已匹配前缀是GT,我们需要开始做判断了:由于模式串当中 pattern[j] != pattern[i-1],即G!=T,最长可匹配前缀子串仍然不存在。
所以当i=2时,j仍然是0,next[2] = 0.
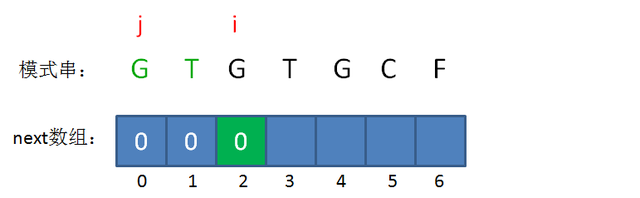
接下来,我们让已匹配前缀子串的长度继续加1.
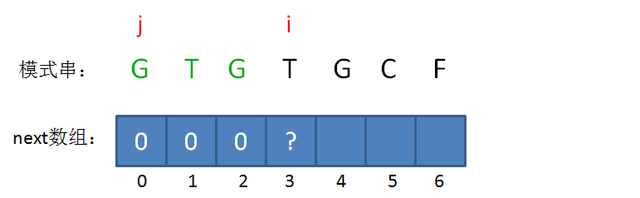
此时的已匹配前缀是GTG,由于模式串当中 pattern[j] = pattern[i-1],即G=G,最长可匹配前缀子串出现了,是G。
所以当i=3时,j=1,next[3] = next[2]+1 = 1。
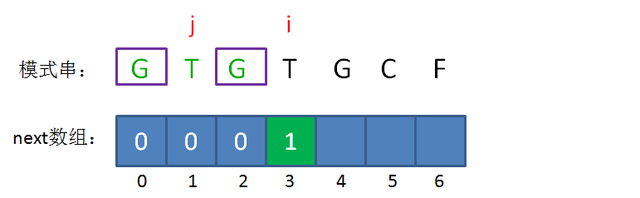
接下来,我们让已匹配前缀子串的长度继续加1
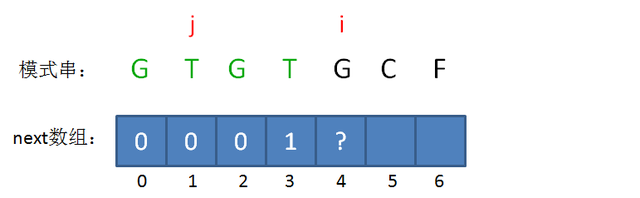
此时的已匹配前缀是GTGT,由于模式串当中 pattern[j] = pattern[i-1],即T=T,最长可匹配前缀子串又增加了一位,是GT。
所以当i=4时,j=2,next[4] = next[3]+1 = 2。

接下来,我们让已匹配前缀子串的长度继续加1:
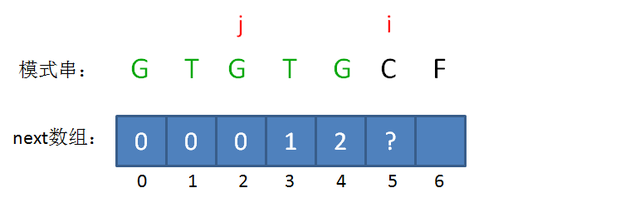
此时的已匹配前缀是GTGTG,由于模式串当中 pattern[j] = pattern[i-1],即G=G,最长可匹配前缀子串又增加了一位,是GTG。
所以当i=5时,j=3,next[5] = next[4]+1 = 3。
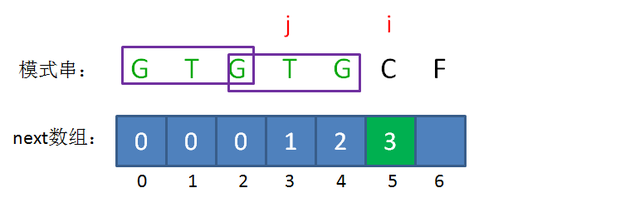
接下来,我们让已匹配前缀子串的长度继续加1
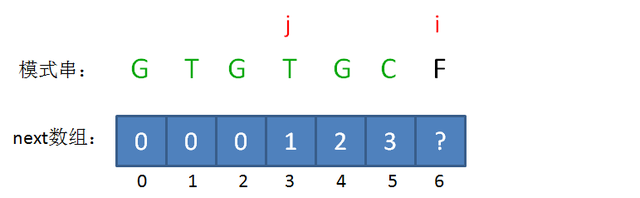
此时的已匹配前缀是GTGTGC,这时候需要注意了,模式串当中 pattern[j] != pattern[i-1],即T != C,这时候该怎么办呢?
这时候,我们已经无法从next[5]的值来推导出next[6],而字符C的前面又有两段重复的子串“GTG”。那么,我们能不能把问题转化一下?
我们可以把计算“GTGTGC”最长可匹配前缀子串的问题,转化成计算“GTGC”最长可匹配前缀子串的问题。
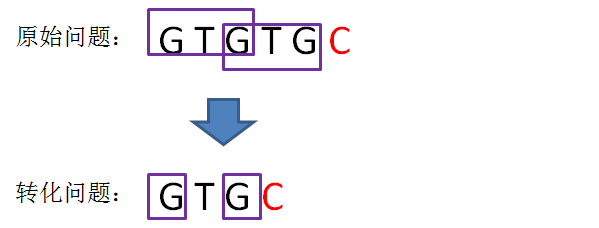
这样的问题转化,也就相当于把变量j回溯到了next[j],也就是j=1的局面(i值不变):
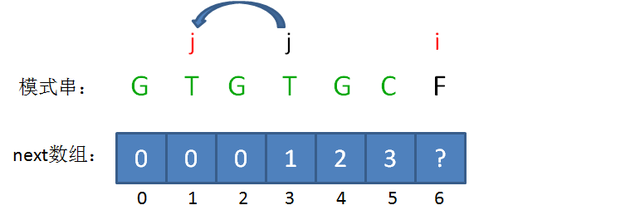
回溯后,情况仍然是 pattern[j] != pattern[i-1],即T!=C。那么我们可以把问题继续进行转化:
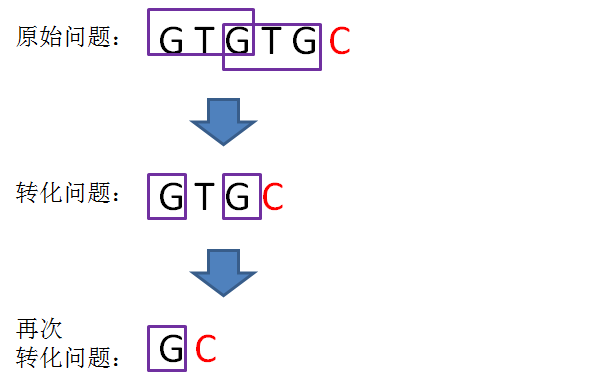
问题再次的转化,相当于再一次把变量j回溯到了next[j],也就是j=0的局面:
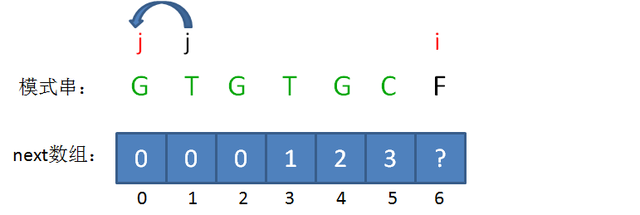
回溯后,情况仍然是 pattern[j] != pattern[i-1],即G!=C。j已经不能再次回溯了,所以我们得出结论:i=6时,j=0,next[6] = 0。


