强化学习七 - Policy Gradient Methods

一.前言

　　之前我们讨论的所有问题都是先学习action value,再根据action value 来选择action(无论是根据greedy policy选择使得action value 最大的action,还是根据ε-greedy policy以1-ε的概率选择使得action value 最大的action,action 的选择都离不开action value 的计算)。即没有action value的估计值就无法进行action选择，也就没有Policy,这类方法被称为 value-based methods.其实我们可以直接产生不依赖于action value 的polcy ,这类直接生成action的方法就叫policy-based methods.他们关系如下：

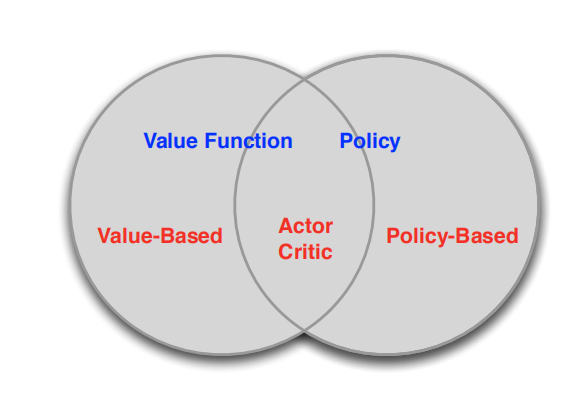
　　value-based方法，需要计算价值函数（value function），根据自己认为的高价值选择行（action）的方法，如Q Learning。
　　policy-based方法，不需要根据value function选择action，可以直接得出policy的方法。
　　图中第三类方法(Actor critic)结合了上述两者，即计算value function，但不直接根据value function选择action，action 由policy-based方法得到。

二. Advantages of Policy-Based RL　　

Policy-Based RL 的优势：

　　1）有着更好的收敛性质。Value_Based 方法需要对值函数进行更新，然后才能反映到策略中，而值函数中的一些小小改变可能会使得策略发生较大改变，从而收敛性较差。当然，我们在模型无关的控制(model free)当中说过，如果将探索因子epsilon设定位1/k,则得到的Monte-carlo Contorl是符合GLIE条件的，此时该方法对应的致函数将收敛于最优值函数。Value-Based方法收敛性较差指得是较容易震荡而难以收敛，而后面说的将收敛于最优值函数是指“最终”将收敛于最优值函数。我们并不知道“最终”是多久，所以，Policy-Based在这个问题上更具有优势。

　　2）在高纬度和连续动作空间上有着逢高的效率。毕竟Value-Based 方法需要计算

如果动作集很大，那么这个max操作的计算量就很大，而Policy-Based RL方法就不存在这种问题。

　　3）可以学习随机性策略。Value-Based 方法是隐式地对策略进行表示，需要用greedy 方法得到策略，所以学习单的是确定性策略。

　　Policy-Based 的缺点：

　　1）通常是收敛到极限；

　　2）评估策略是低效，高差异的；

　　举个例子1，在我们所熟知的“石头剪刀布”游戏中，需要寻求纳什均衡，所以并不能弄一个确定性策略，这种情况下，一个均匀的随机策略就是最优的。

　　举例2：

　　

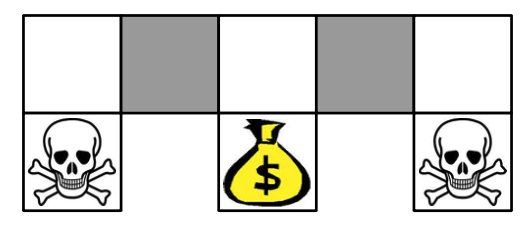
在上面的这个格子世界中，两个灰色方格对于智能体而言并没有什么区别。如果使用一个确定性策略，那么在灰色方格处的决策要么都向左，要么都向右，不管是向左还是向右，都有可能卡住，如下图：

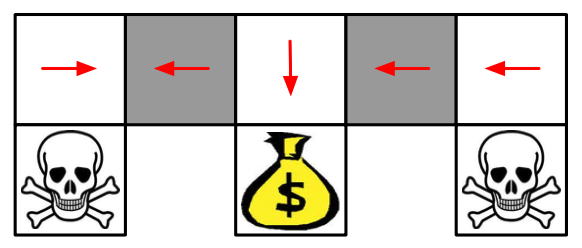
当然，Value-Based方法也可以学习一个near-deterministic(近似确定性)策略，比如说epsilon-greedy，这样的方法虽然不会一直卡住，但是一般需要较长时间才能结束这一episode。课程中有这么一句话：Whenever stochastic policy occurs, a stochastic policy can do better than a deterministic policy。也就是说，一般而言，只要出现随机性策略的时候，一般都会比确定性策略要好。

下面来看一下常用的几个目标函数：

        1）episodic环境中，我们使用start value：

2）continuing环境中，我们使用average value：

 

 3）continuing环境中，也可以使用average reward per time-step：

其中d为利用对应策略生成的马尔可夫链的稳态分布。1）中为从某个状态开始，看一下后面将得到的奖励；2）中为continuing环境，所以并没有一个所谓的初始状态，也没有一个结束状态；3）中表示平稳状态分布下单步的奖励。这三种策略殊途同归，最后都运用到了策略下降方面；

 三. Score Function

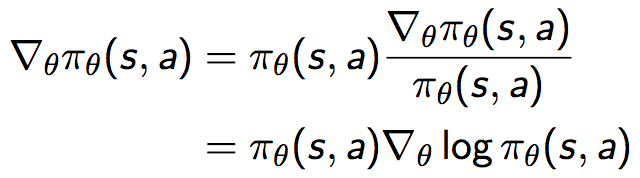
也即策略梯度可以等价地表示为策略乘以一个似然函数的倒数，这个与极大似然操作形式一致的式子叫做Score Function ,表示为：

 

下面通过两个例子说明score function:

　　1)softmax policy

首先假设使用线性特征组合对动作进行加权：

此时，score function为：

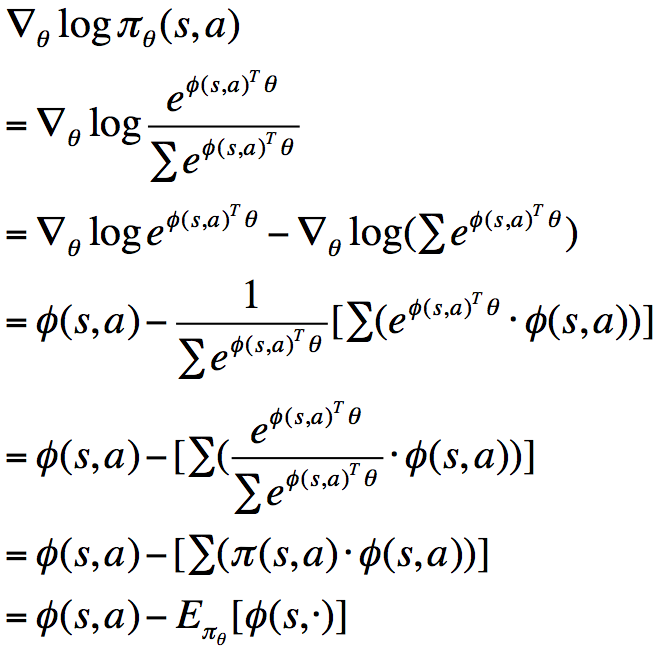
2）同理，我们可以得到服从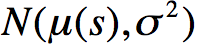的高斯分布的score function：

 

四.one-step MDP

考虑完策略的导数之后，接着我们讨论奖励函数的导数。首先考虑一个简单的one-step MDP：

 推导奖励函数的梯度：

 通过选取一个动作来使奖励最大化，选取的正确方法可能取决于状态和动作；

我们通过这个简单的one-step MDP可知，奖励函数的导数等于socre function乘以reward在策略下的期望，也即：

 　　要找到策略梯度，我们要掌握怎样调整策略参数的方法才可以在无论何种状态的情况下，选取优质的动作，我们可以调整选取动作的方法来得到更多的奖励。要这样首先就要从选取的目标函数开始，在one step案例中我们讨论过的三个目标函数本质上是相同的，我们的目标就是要应用策略所得到的预期奖励，所以我们要能够找到让我们获得最佳预期的参数。我们身处任意一个状态时，根据策略选取动作，我们的期望就是获得的最大奖励；策略梯度定理正是这一简单情形的拓展：

与上面的one-step MDP的情形相比，这里将其拓展到了multi-step MDP，并且将即时奖励r替换为了long-term值函数，这一定理非常重要。我们知道，我们对于策略参数的更新都是沿着极大化奖励函数的方向进行的，所以由上式我们可以对参数进行更新。

接下来将将该定理结合model-free情形进行使用，得到REINFORCE算法：

五.Monte-Carlo Policy Gradient (REINFORCE)

其想法非常简单，就是将奖励函数的梯度中的期望换为采样，在一个episode结束之后，利用该episode中的每一个step对参数进行更新。不过这个算法中对于的估计使用的是回报（return），这是一个无偏估计，但是却有着较大的方差，所以，我们考虑换成其他方法对值函数进行逼近，比如说利用神经网络或其他参数化方法，记参数为w（此处可回想DDPG算法形式）：

 

　　我们称之为Critic，并将上面的参数化策略称为Actor，将这二者结合起来，叫做Actor-Critic算法：

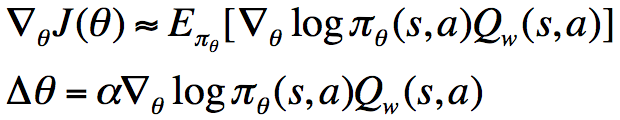
对于参数w的更新，我们可以将回报（return）或者TD target作为目标，最小化当前值函数与目标的平方。此外，在Actor-Critic算法中，我们可以在每个step对策略进行更新，而不用像REINFORCE一样，只能在每个episode运行完成之后进行更新。因为这里每个step我们可以使用对奖励进行估计，然后代入上面的式子，对策略进行更新，而REINFORCE使用回报（return）决定了它不能实时更新。

        Actor-Critic算法虽然降低了方差，但是一般来说是有偏的，因为在approximating(逼近)的时候引入了bias(误差)。那是否能够通过恰当地选择值函数估计器来避免引入bias呢？这是可以的。由此我们引出兼容函数估计（Compatible Function Approximation）

 考虑条件1中提到的式子，用语言表述为：“score function = the gradient of Critic”，将其代入到中，可得：

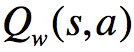
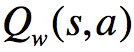
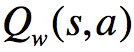
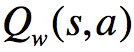
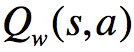
 比方说，在某个状态s和动作a下，假设为正，则沿着的梯度方向进行更新，且越大，越大，如果为负，则朝着与的梯度相反的方向更新。换句话说，我们这里的朝着大的方向更新，

 

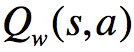
        前面我们说过，为了降低REINFORCE算法的方差，我们引入了Critic，现在，我们进一步使用Baseline来降低RL中的方差。首先我们可以推导出如下式子：

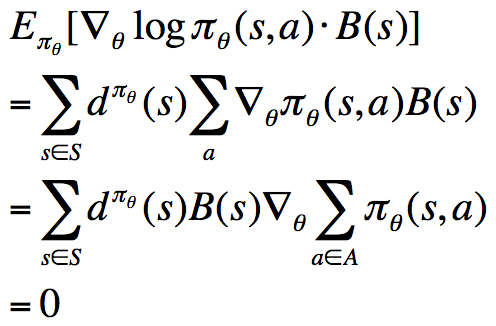
该式表明，对于某一个与动作a无关的基准函数B(s)，它乘以score function之后，计算在策略下的期望，结果为0。换句话说，我们可以在奖励函数的梯度的基础上任意的增减一个这样的式子，而保持梯度不变。一个不错的Baseline函数就是值函数，在原奖励函数梯度的计算式上减去该值，得到：

我们称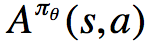为优势函数，用其表示奖励函数的梯度为：

  优势函数的意义是，在动作值函数的基础上减去了对应状态拥有的基准值，使之变为动作带来的增益，因而降低了方差（降低了由于状态基准值的抖动引起的方差）。

        现在我们给出的计算优势函数的公式是理论上的，或者说是策略对应的真实优势函数，但实际上，我们并不知道该函数，因而只能对其进行估计，就像我们前面估计状态值函数和动作值函数一样：

我们可以不断地更新以及，比方说利用TD方法进行更新，然后通过计算得到。不过令人感到不开心的是，这里我们需要维持两个逼近器，有没有方法能够让我们用一个逼近器就能够给出优势函数的估计呢？有的，具体见下面的PPT：

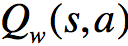
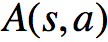
 δπθ=reward+下一个状态真实价值折扣-现在所处的状态；

其中最为重要的结论是：“如果我们使用真实的状态值函数来计算TD error，则TD error为优势函数的一个无偏估计”。并且，在这种方法中，我们仅需一组参数就能够对优势函数进行估计。

        最后我们介绍一下自然策略梯度：

 

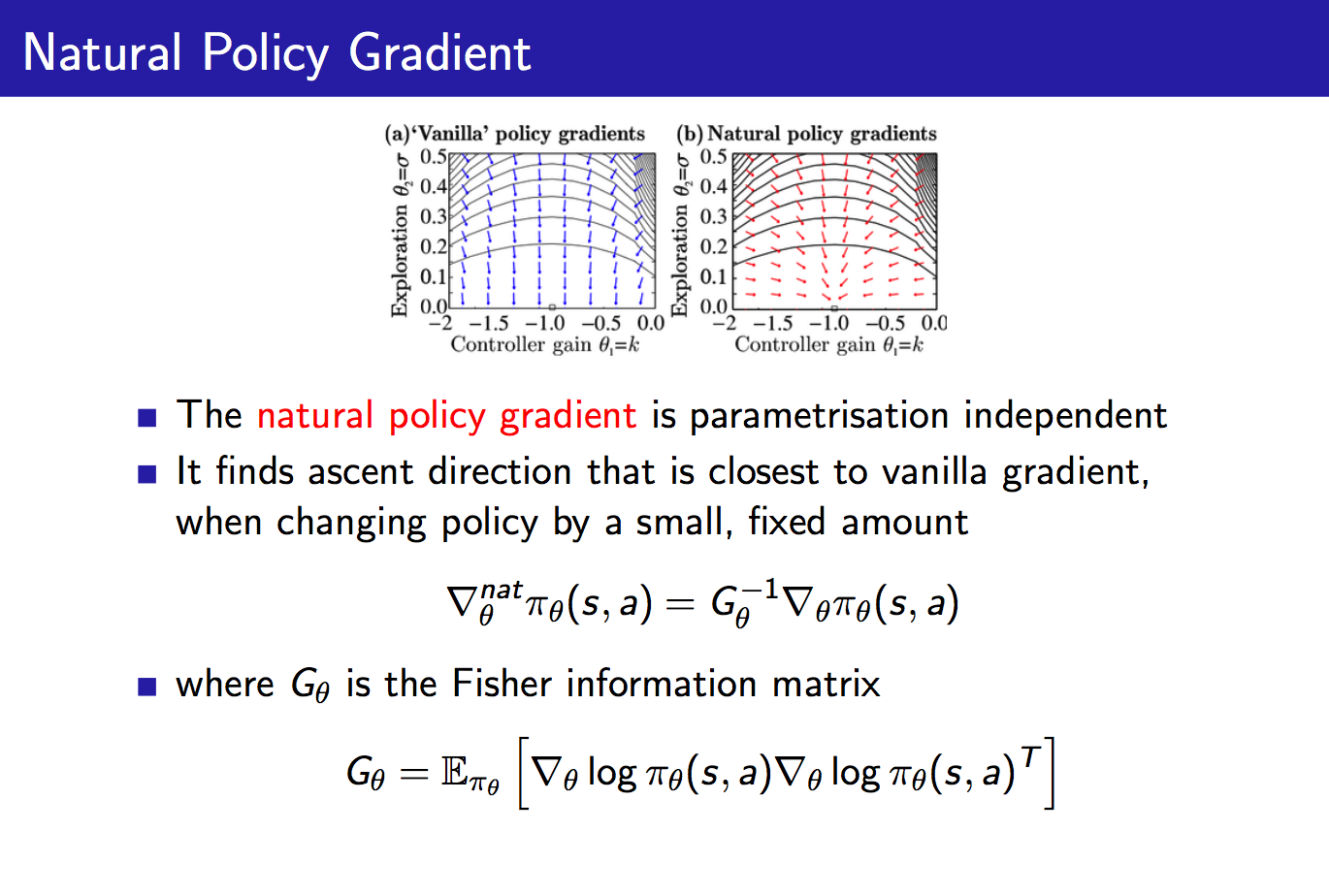
自然策略梯度也即直接对原始策略梯度进行修正，乘以一个Fisher信息阵。这样做有什么用处呢？它使得策略梯度变成参数化无关的了。举个例子，对于一个softmax策略，我们增大其中所有动作的score，此时各个动作的概率并不会发生改变，这可以通过其score function来考虑。

        比方说，我们反过来想，成比例的增大策略中各个动作对应的分子，因为softmax策略中的分母也会成比例的增大，所以最终各个动作的概率并没有发生改变。如果这里我们是通过增加来增加分子的值的，所以上面的score function也可能会随之增大，这样的话，虽然该策略各个动作对应的概率没有变，但是下一步对于策略的改进却发生了改变（想想对于策略参数的更新公式），这并不是我们想看到的。而自然策略梯度可以很好地解决这一问题，对于刚刚提及的这种情形，Fisher信息阵也将增大，从而使得下一步对于策略的改进与重新参数化无关，就很开心了。

 将自然策略梯度与Actor-Critic结合，得到Natural Actor-Critic如下：

在上面的推导中，我们可以将compatible function approximation积分代入对于奖励函数的求导中，得到最终的奖励函数的自然梯度，发现它就等于Critic的参数w，这并不是巧合，当我们结合natural policy gradient + compatible function approximation（自然策略梯度+相容函数逼近）之后，就可以得到这一结论：对Actor参数的更新就等于Critic的参数。

总结：　

本章阐述了value-based methods和policy-based methods的优缺点，引入了性能函数J(θ) ，介绍了PG定理，并详细介绍了episode case下的PG方法：REINFORCE 、REINFORCE-with-baseline(减小偏差，但方差较大)。介绍了结合PG 和value-based methods的Actor-Critic Methods，以及 continuing case下的PG。