BZOJ 3091 城市旅行 (LCT)
3091: 城市旅行
Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 2251 Solved: 761
[Submit][Status][Discuss]
Description
.jpg)
Input
.jpg)
Output
![]()
Sample Input
1 3 2 5
1 2
1 3
2 4
4 2 4
1 2 4
2 3 4
3 1 4 1
4 1 4
Sample Output
6/1
HINT
对于所有数据满足 1<=N<=50,000 1<=M<=50,000 1<=Ai<=10^6 1<=D<=100 1<=U,V<=N
Source
题解:
给出一个无根树,维护四个操作,link,cut,路径加法,路径期望查询,前三个都是LCT的基本操作(LCT见前面的随笔),主要说第四个;
对于路径期望,如果两点之间的点数为n,那么很明显是C(n+1,2)=n*(n+1)/2;考虑维护分子:
如图所示,考虑求每个点的贡献,然后求和;第一个点对答案的贡献为a1*1*n(左端点只能选a1,右端点可以选a1~an),
第二个点对答案的贡献为a2*2*(n-1)(左端点可以选a1或a2,右端点可以选a2~an)
于是答案就是a1*1*n+a2*2*(n-1)+...+an*n*1 这个东西显然不能暴力求 需要在LCT上维护 但是直接维护根本维护不了 怎么办呢?
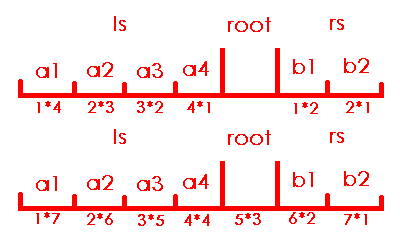
观察左子树 将左子树合并前后的贡献值作差可得
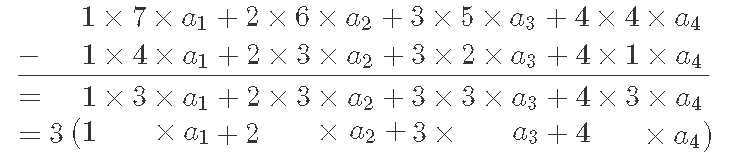
我们发现这个3其实就是右子树的size+1
于是我们们令lsum=1*a1+2*a2+3*a3...+n*an; rsum=n*a1+(n-1)*a2+...+1*an;
则:root.ans=lson.ans+lson.lsum*(rson.size+1) + rson.ans+rson.rsum*(lson.size+1) + root.sum*(lson.size+1)*(rson.size+1) (左子树贡献+右子树的贡献+根节点的贡献);
考虑对于lsum和rsum的维护,lsum的维护为root.lsum = lson.lsum+root.val*(lson.size+1) + rson.lsum + rson.sum*(lson.size+1);
对于rsum 的维护类似: root.rsum = rson.rsum + root.val*(son.size+1) + lson.rsum + lson.sum*(rson.size+1);
当对于root为根的整棵树更新的时候root.ans的维护为:加 val*(1*n+2*(n-1)+3*(n-2)+...+n*1)=val*n*(n+1)*(n+2)/6(这里的n=root.size)。
1$*$n+2$*$(n-1)+3$*$(n-2)+...+n$*$1
=(1+2+3+...+n)$*$n-(1$*$2+2$*$3+3$*$4+...+(n-1)$*$n)
=${n^2*(n+1)\over 2}$-(1$^2$+2$^2$+3$^2$+...+(n-1)$^2$+1+2+3+...+(n-1))
=$n^2*(n+1)\over 2$-$n*(n-1)*(2*n-1)\over 6$ -$n*(n-1)\over 2$
=$(3*n(n+1)-n*(n-1)*(2*n-1)-3*n*(n-1))\over 6$
=$n*(n^2+3*n+2)\over 6$
=$n*(n+1)*(n+2)\over 6$
参考代码:

1 /************************************************************** 2 Problem: 3091 3 User: SongHL 4 Language: C++ 5 Result: Accepted 6 Time:1764 ms 7 Memory:6464 kb 8 ****************************************************************/ 9 10 //BZOJ 3091 11 //给出一棵无根树,维护四个操作:link,cut,路径加法,路径期望查询 12 #include<bits/stdc++.h> 13 #define LL long long 14 #define inf 2147483640 15 #define Pi acos(-1.0) 16 using namespace std; 17 const int maxn=50010; 18 int n,m,fa[maxn]; 19 struct node{ 20 int son[2]; 21 LL sum,tag,rev,ans,val,lsum,rsum,size; 22 int& operator [] (int x) {return son[x];} 23 }tree[maxn]; 24 LL gcd(LL a,LL b) {return b==0 ? a : gcd(b,a%b);} 25 namespace LCT{ 26 void reverse(int k) 27 { 28 swap(tree[k][0],tree[k][1]); 29 swap(tree[k].lsum,tree[k].rsum); 30 tree[k].rev^=1; 31 } 32 33 void add(int k,LL val) 34 { 35 tree[k].val+=val; 36 tree[k].sum+=tree[k].size*val; 37 tree[k].tag+=val; 38 tree[k].ans+=tree[k].size*(tree[k].size+1)*(tree[k].size+2)/6*val; 39 tree[k].lsum+=tree[k].size*(tree[k].size+1)/2*val; 40 tree[k].rsum+=tree[k].size*(tree[k].size+1)/2*val; 41 } 42 int find(int x) {return fa[x] ? find(fa[x]):x;} 43 44 void pushdown(int k) 45 { 46 if(tree[fa[k]][0]==k || tree[fa[k]][1]==k) pushdown(fa[k]); 47 int l=tree[k][0],r=tree[k][1]; 48 if(tree[k].rev) 49 { 50 if(l) reverse(l); 51 if(r) reverse(r); 52 tree[k].rev^=1; 53 } 54 if(tree[k].tag) 55 { 56 if(l) add(l,tree[k].tag); 57 if(r) add(r,tree[k].tag); 58 tree[k].tag=0; 59 } 60 } 61 void pushup(int k) 62 { 63 int l=tree[k][0],r=tree[k][1]; 64 tree[k].size=tree[l].size+tree[r].size+1; 65 tree[k].lsum=tree[l].lsum+(tree[l].size+1)*tree[k].val+tree[r].lsum+tree[r].sum*(tree[l].size+1); 66 tree[k].rsum=tree[r].rsum+(tree[r].size+1)*tree[k].val+tree[l].rsum+tree[l].sum*(tree[r].size+1); 67 tree[k].sum=tree[l].sum+tree[r].sum+tree[k].val; 68 tree[k].ans=tree[l].ans+tree[r].ans+tree[l].lsum*(tree[r].size+1)+tree[r].rsum*(tree[l].size+1)+tree[k].val*(tree[l].size+1)*(tree[r].size+1); 69 } 70 void rotate(int x) 71 { 72 int y=fa[x],z=fa[y],l,r; 73 l=tree[y][1]==x;r=l^1; 74 if(tree[z][0]==y || tree[z][1]==y) tree[z][tree[z][1]==y]=x; 75 fa[tree[x][r]]=y;fa[x]=z;fa[y]=x; 76 tree[y][l]=tree[x][r];tree[x][r]=y; 77 pushup(y);pushup(x); 78 } 79 void splay(int x) 80 { 81 pushdown(x); 82 while(tree[fa[x]][0]==x || tree[fa[x]][1]==x) 83 { 84 int y=fa[x],z=fa[y]; 85 if(tree[z][0]==y || tree[z][1]==y) 86 { 87 if(tree[z][0]==y^tree[y][0]==x) rotate(x); 88 else rotate(y); 89 } 90 rotate(x); 91 } 92 } 93 void access(int x) //访问 94 { 95 for(int y=0;x;y=x,x=fa[x]) splay(x),tree[x][1]=y,pushup(x); 96 } 97 int findroot(int x)//找根(在真实的树中的) 98 { 99 access(x);splay(x); 100 while(tree[x][0]) pushdown(x),x=tree[x][0]; 101 return x; 102 } 103 void makeroot(int x) //换根 104 { 105 access(x);splay(x);reverse(x); 106 } 107 void split(int x,int y)//提取路径 108 { 109 makeroot(x); 110 access(y);splay(y); 111 } 112 void link(int x,int y) 113 { 114 makeroot(x);fa[x]=y; 115 } 116 void cut(int x,int y) 117 { 118 makeroot(x);access(y);splay(y); 119 if(tree[y][0]==x && tree[x][1]==0) 120 tree[y][0]=0,fa[x]=0,pushup(y); 121 } 122 void modify(int x,int y,LL val)//对x~y这段路径操作 123 { 124 makeroot(x);access(y); 125 splay(y);add(y,val); 126 } 127 void query(int x,int y) 128 { 129 split(x,y); 130 LL A=tree[y].ans,B=tree[y].size*(tree[y].size+1)/2; 131 LL D=gcd(A,B); 132 printf("%lld/%lld\n",A/D,B/D); 133 } 134 } 135 using namespace LCT; 136 137 int main() 138 { 139 scanf("%d%d",&n,&m); 140 for(int i=1;i<=n;i++) scanf("%lld",&tree[i].val); 141 for(int u,v,i=1;i<n;i++) 142 { 143 scanf("%d%d",&u,&v); 144 link(u,v); 145 } 146 for(int op,x,y,d,i=1;i<=m;i++) 147 { 148 scanf("%d%d%d",&op,&x,&y); 149 if(op==1) if(find(x)==find(y)) cut(x,y); 150 if(op==2) if(find(x)!=find(y)) link(x,y); 151 if(op==3){ scanf("%d",&d); if(find(x)==find(y)) modify(x,y,d); } 152 if(op==4) if(find(x)==find(y)) query(x,y); else puts("-1"); 153 } 154 return 0; 155 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号