LCT（Link Cut Tree）总结

概念、性质简述

首先介绍一下链剖分的概念
链剖分，是指一类对树的边进行轻重划分的操作，这样做的目的是为了减少某些链上的修改、查询等操作的复杂度。
目前总共有三类：重链剖分，实链剖分和并不常见的长链剖分。

重链剖分

实际上我们经常讲的树剖，就是重链剖分的常用称呼。
对于每个点，选择最大的子树，将这条连边划分为重边，而连向其他子树的边划分为轻边。
若干重边连接在一起构成重链，用树状数组或线段树等静态数据结构维护。
这里就不赘述；

实链剖分

同样将某一个儿子的连边划分为实边，而连向其他子树的边划分为虚边。
区别在于虚实是可以动态变化的，因此要使用更高级、更灵活的Splay来维护每一条由若干实边连接而成的实链。
基于性质更加优秀的实链剖分，LCT(Link-Cut Tree)应运而生。
LCT维护的对象其实是一个森林。
在实链剖分的基础下，LCT资磁更多的操作

同样将某一个儿子的连边划分为实边，而连向其他子树的边划分为虚边。
区别在于虚实是可以动态变化的，因此要使用更高级、更灵活的Splay来维护每一条由若干实边连接而成的实链。
基于性质更加优秀的实链剖分，LCT(Link-Cut Tree)应运而生。
LCT维护的对象其实是一个森林。
在实链剖分的基础下，LCT资磁更多的操作

  • 查询、修改链上的信息（最值，总和等）
  • 随意指定原树的根（即换根）
  • 动态连边、删边
  • 合并两棵树、分离一棵树
  • 动态维护连通性
  • 更多意想不到的操作（可以往下滑一滑）

LCT的主要性质如下：

    1. 每一个Splay维护的是一条从上到下按在原树中深度严格递增的路径，且中序遍历Splay得到的每个点的深度序列严格递增。
      比如有一棵树，根节点为1（深度1），有两个儿子2,3（深度2），那么Splay有3种构成方式：
      {1−2},{3}
      {1−3},{2}
      {1},{2},{3}（每个集合表示一个Splay）
      而不能把1,2,3同放在一个Splay中（存在深度相同的点）

    2. 每个节点包含且仅包含于一个Splay中

                      边分为实边和虚边，实边包含在Splay中，而虚边总是由一棵Splay指向另一个节点（指向该Splay中中序遍历最靠前的点在原树中的父亲）。
                      因为性质2，当某点在原树中有多个儿子时，只能向其中一个儿子拉一条实链（只认一个儿子），而其它儿子是不能在这个Splay中的。
                      那么为了保持树的形状，我们要让到其它儿子的边变为虚边，由对应儿子所属的Splay的根节点的父亲指向该点，而从该点并不能直接访问该儿子（认父不认子）。

各种操作

access(x)

LCT核心操作，也是最难理解的操作。其它所有的操作都是在此基础上完成的。
因为性质3，我们不能总是保证两个点之间的路径是直接连通的（在一个Splay上）。
access即定义为打通根节点到指定节点的实链，使得一条中序遍历以根开始、以指定点结束的Splay出现。
所以还是来几张图吧。
下面的图片参考YangZhe的论文
有一棵树，假设一开始实边和虚边是这样划分的（虚线为虚边）

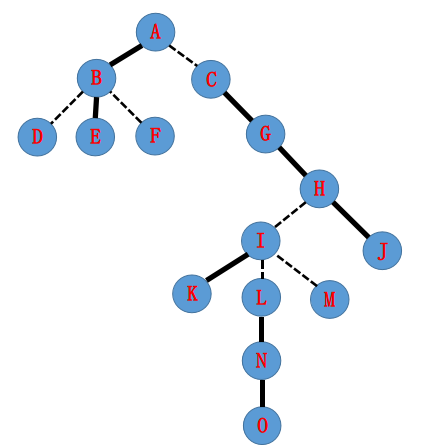
那么所构成的LCT可能会长这样（绿框中为一个Splay，可能不会长这样，但只要满足中序遍历按深度递增（性质1）就对结果无影响）

 

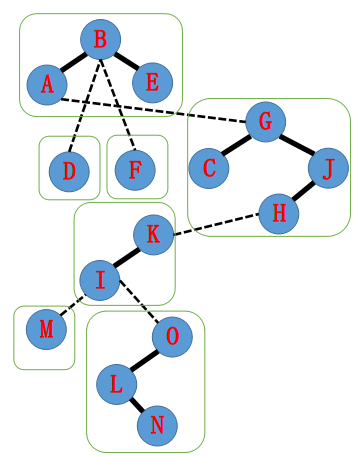
现在我们要access(N)，把A−N的路径拉起来变成一条Splay。
因为性质2，该路径上其它链都要给这条链让路，也就是把每个点到该路径以外的实边变虚。
所以我们希望虚实边重新划分成这样。

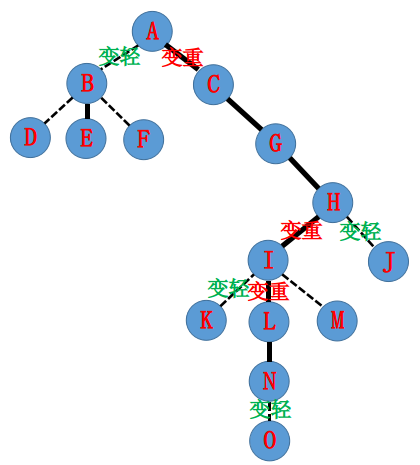
然后怎么实现呢？
我们要一步步往上拉。
首先把splay(N)，使之成为当前Splay中的根。
为了满足性质2，原来N−O的重边要变轻。
因为按深度O在N的下面，在Splay中O在N的右子树中，所以直接单方面将N的右儿子置为0（认父不认子）
然后就变成了这样——

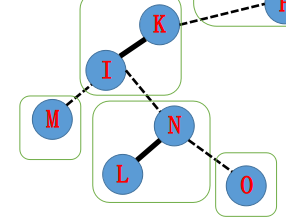
我们接着把N所属Splay的虚边指向的I（在原树上是L的父亲）也转到它所属Splay的根，splay(I)。
原来在II下方的重边I−K要变轻（同样是将右儿子去掉）。
这时候I−L就可以变重了。因为L肯定是在I下方的（刚才L所属Splay指向了I），所以I的右儿子置为N，满足性质1。
然后就变成了这样——

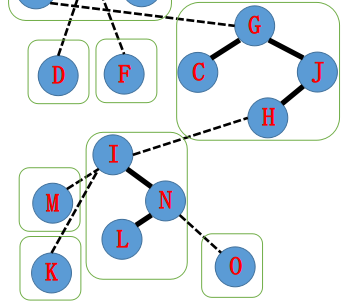
I指向H，接着splay(H)，H的右儿子置为I。

 

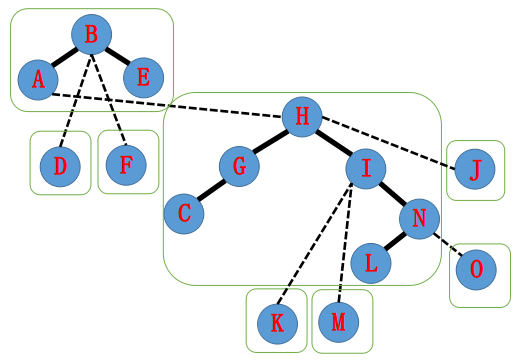
H指向A，接着splay(A)，A的右儿子置为H。

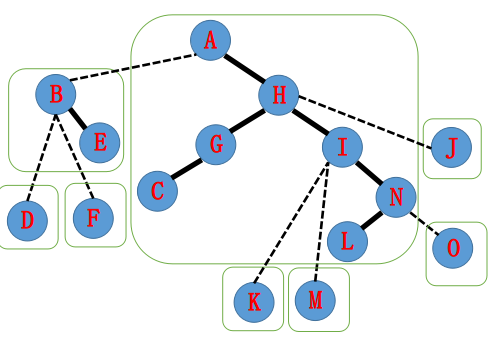
A−N的路径已经在一个Splay中了，大功告成！
代码其实很简单。。。。。。循环处理，只有四步——

    1. 转到根；
    2. 换儿子；
    3. 更新信息；
    4. 当前操作点切换为轻边所指的父亲，转1
1 inline void access(int x){
2     for(int y=0;x;y=x,x=f[x])
3         splay(x),c[x][1]=y,pushup(x);//儿子变了，需要及时上传信息
4 }
View Code

makeroot(x)

只是把根到某个节点的路径拉起来并不能满足我们的需要。更多时候，我们要获取指定两个节点之间的路径信息。
然而一定会出现路径不能满足按深度严格递增的要求的情况。根据性质1，这样的路径不能在一个Splay中。
Then what can we do?
makeroot定义为换根，让指定点成为原树的根。
这时候就利用到access(x)和Splay的翻转操作。
access(x)后xx在Splay中一定是深度最大的点对吧。
splay(x)后，x在Splay中将没有右子树（性质1）。于是翻转整个Splay，使得所有点的深度都倒过来了，x没了左子树，反倒成了深度最小的点（根节点），达到了我们的目的。
代码

1 inline void makeroot(RI x){//换根
2     access(x);splay(x);
3     pushr(x);
4 }
View Code

 

关于pushdown和makeroot的一个相关的小问题详见下方update（关于pushdown的说明）

findroot(x)

找x所在原树的树根，主要用来判断两点之间的连通性（findroot(x)==findroot(y)表明x,y在同一棵树中）
代码：

1 inline int findroot(RI x){//找根（在真实的树中的）
2     access(x);splay(x);
3     while(c[x][0]) pushdown(x),x=c[x][0];
4     return x;
5 }
View Code

同样利用性质1，不停找左儿子，因为其深度一定比当前点深度小。

split(x,y)

神奇的makeroot已经出现，我们终于可以访问指定的一条在原树中的链啦！
split(x,y)定义为拉出x−y的路径成为一个Splay（窝以y作为该Splay的根）
代码

1 inline void split(int x,int y){
2     makeroot(x);
3     access(y);splay(y);
4 }
View Code

　　

x成为了根，那么x到y的路径就可以用access(y)直接拉出来了，将y转到Splay根后，我们就可以直接通过访问y来获取该路径的有关信息

link(x,y)

连一条x−y的边（窝使x的父亲指向y，连一条轻边）
代码

1 inline bool link(int x,int y){
2     makeroot(x);
3     if(findroot(y)==x)return 0;//两点已经在同一子树中，再连边不合法
4     f[x]=y;
5     return 1;
6 }
View Code

 

　如果题目保证连边合法，代码就可以更简单

1 inline void link(int x,int y){
2     makeroot(x);
3     f[x]=y;
4 }
View Code

　　

cut(x,y)

将x−y的边断开。
如果题目保证断边合法，倒是很方便。
使xx为根后，y的父亲一定指向x，深度相差一定是1。当access(y),splay(y)以后，x一定是y的左儿子，直接双向断开连接

1 inline void cut(int x,int y){
2     split(x,y);
3     f[x]=c[y][0]=0;
4     pushup(y);//少了个儿子，也要上传一下
5 }
View Code

 

　那如果不一定存在该边呢？
充分利用好Splay和LCT的各种基本性质吧！
正确姿势——先判一下连通性，再看看x,yx,y是否有父子关系，还要看xx是否有右儿子。
因为access(y)以后，假如y与x在同一Splay中而没有直接连边，那么这条路径上就一定会有其它点，在中序遍历序列中的位置会介于x与y之间。
那么可能x的父亲就不是y了。
也可能x的父亲还是y，那么其它的点就在x的右子树中，就像这样

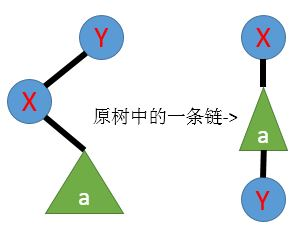
只有三个条件都满足，才可以断掉。

1 inline bool cut(int x,int y){
2     makeroot(x);
3     if(findroot(y)!=x||f[x]!=y||c[x][1])return 0;
4     f[x]=c[y][0]=0;
5     pushup(y);
6     return 1;
7 }
View Code

 

　　如果维护了size，还可以换一种判断

1 inline bool cut(int x,int y){
2     makeroot(x);
3     if(findroot(y)!=x||sz[y]>2)return 0;
4     f[x]=c[y][0]=0;
5     pushup(y);
6 }
View Code

 

　　解释一下，如果他们有直接连边的话，access(y)以后，为了满足性质1，该Splay只会剩下x,y两个点了。
反过来说，如果有其它的点，size不就大于2了么？

其实，还有一些LCT中的Splay的操作，跟我们以往学习的纯Splay的某些操作细节不甚相同。
包括splay(x),rotate(x),nroot(x)（看到许多版本LCT写的是isroot(x)，但我觉得反过来会方便些）
这些区别之处详见下面的模板题注释。

update（关于findroot中pushdown的说明）

找根的时候，当然不能保证Splay中到根的路径上的翻转标记全放掉。
所以最好把pushdown写上。
Candy巨佬的总结对pushdown问题有详细的分析

1 makeroot(x);
2 if(findroot(y)==x)//后续省略
View Code

 

　　这样好像没出过问题，那应该可以证明是没问题的（makeroot保证了x在LCT的顶端，access(y)+splay(y)以后，假如x,y在一个Splay里，那x到y的路径一定全部放完了标记）
导致很久没有发现错误。。。。。。
另外提一下，假如LCT题目在维护连通性的情况中只可能出现合并而不会出现分离的话，其实可以用并查集哦！（实践证明findroot很慢）
这样的例子有不少，比如下面“维护链上的边权信息”部分的两道题都是的。
甚至听到Julao们说有少量题目还专门卡这个细节。。。。。。XZY巨佬的博客就提到了

update（关于pushdown的说明）

pushdown和makeroot有时候会这样写，常数小一点

 1 void pushdown(int x){
 2     if(r[x]){
 3         r[x]=0;
 4         int t=c[x][0];
 5         r[c[x][0]=c[x][1]]^=1;
 6         r[c[x][1]=t]^=1;
 7     }
 8 }
 9 void makeroot(int x){
10     access(x);splay(x);
11     r[x]^=1;
12 }
View Code

这种写法等于说当x有懒标记时，x的左右儿子还是反的

再次update，发现这种问题还是可以避免的，若用这种pushdown，findroot可以写，这样写就好啦

1 inline int findroot(int x){
2     access(x);splay(x);
3     pushdown(x);
4     while(lc)pushdown(x=lc);
5     splay(x);
6     return x;
7 }
View Code

　　所以此总结以及下面模板里的pushdown，常数大了一点点，却是更稳妥、严谨的写法

 1 //pushr同上方makeroot部分
 2 void pushdown(int x){
 3     if(r[x]){
 4         if(c[x][0])pushr(c[x][0]);//copy自模板，然后发现if可以不写
 5         if(c[x][1])pushr(c[x][1]);
 6         r[x]=0;
 7     }
 8 }
 9 void makeroot(int x){
10     access(x);splay(x);
11     pushr(x);//可以看到两种写法造成makeroot都是不一样的
12 }
View Code

　　

这种写法等于说当x有懒标记时，x的左右儿子已经放到正确的位置了，只是儿子的儿子还是反的
那么这样就不会出问题啦
两种写法差别还确实有点大呢
当题目中维护的信息与左右儿子顺序有关的时候，pushdown如果用这种不严谨写法会是错的
比如[NOI2005]维护数列（这是Splay题）和洛谷P3613 睡觉困难综合征

update（关于findroot中splay(x)的说明）

某位Julao指出findroot中在找到原树根后（此时x跳到了原树根）应splay(x)，伸展一下，Splay的特性，保证复杂度(好像牵涉到玄学的势能分析，什么也不会啊QvQ)
非常正确的做法。于是进行了更正，却忘记了进行验证。
后来Destinies巨佬指出第8个点WA。
经过验证之后发现，加上splay(x)以后，点的相对位置发生了变化，导致cut需要更改，更改如下：

1 inline void cut(register int x,register int y){//断边
2     makeroot(x);
3     if(findroot(y)==x&&f[y]==x&&!c[y][0]){
4         f[y]=c[x][1]=0;//x在findroot(y)后被转到了根
5         pushup(x);
6     }
7 }
View Code

　　

为了避免频繁讨论、修改带来的繁琐，此总结不建议在此模板题里加上splay(x)
因为确实很难找到卡掉不写splay(x)的代码的数据，而且可能带来一点常数。
或许我大多数时候把splay写成单旋（没错就是HNOI2017那种）会比Zig、Zag双旋要快个十几分之一也是这样的道理吧。。。。。。
但这不意味着就不用写了
在比较关键的时候（比如比赛时）该写的总要写。
不管是单旋，还是不splay(x)，都是很容易卡掉的。。。。。。
相信Dalao们都能熟练地在很多种不同的写法中切换的

模板

最基本的LCT操作都在这里，也没有更多额外的复杂操作了.

要求：

给定n个点以及每个点的权值，要你处理接下来的m个操作。操作有4种。操作从0到3编号。点从1到n编号。

0：后接两个整数(x，y)，代表询问从x到y的路径上的点的权值的xor和。保证x到y是联通的。

1：后接两个整数(x，y)，代表连接x到y，若x到y已经联通则无需连接。

2：后接两个整数(x，y)，代表删除边(x，y)，不保证边(x，y)存在。

3：后接两个整数(x，y)，代表将点x上的权值变成y。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define RI register int
 4 inline int read()
 5 {
 6     int f=1,x=0;char ch=getchar();
 7     while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
 8     while(ch>='0'&&ch<='9'){ x=x*10+ch-'0'; ch=getchar(); }
 9     return f*x;
10 }
11 const int N=300009;
12 int f[N],c[N][2],v[N],s[N],st[N];
13 bool r[N];
14 //判断节点是否为一个Splay的根(与普通Splay的区别1) 
15 //原理很简单，如果连的是轻边，他的父亲的儿子里没有它
16 inline bool nroot(RI x){ return c[f[x]][0]==x || c[f[x]][1]==x; }
17 inline void pushup(RI x){ s[x]=s[c[x][0]]^s[c[x][1]]^v[x]; }//上传信息
18 inline void pushr(RI x){ RI t=c[x][0];c[x][0]=c[x][1];c[x][1]=t;r[x]^=1; }//翻转操作
19 inline void pushdown(RI x)//判断并释放懒标记
20 {
21     if(r[x])
22     {
23         if(c[x][0]) pushr(c[x][0]);
24         if(c[x][1]) pushr(c[x][1]);
25         r[x]=0;
26     }
27 }
28 inline void rotate(RI x)//一次旋转
29 {
30     RI y=f[x],z=f[y],k = c[y][1]==x,w=c[x][!k];
31     if(nroot(y)) c[z][c[z][1]==y]=x; c[x][!k]=y;c[y][k]=w;
32     //额外注意if(nroot(y))语句此处不判断会引起致命错误(与普通Splay的区别2)
33     if(w) f[w]=y; f[y]=x;f[x]=z;
34     pushup(y);
35 }
36 inline void splay(RI x)//只传了一个参数因为所有操作的目标都是该Splay的根(与普通Splay的区别3)
37 {
38     RI y=x,z=0;
39     st[++z]=y;//st为栈，暂存当前点到根的整条路径，pushdown时一定要从上往下放标记（与普通Splay的区别4）
40     while(nroot(y)) st[++z]=y=f[y];
41     while(z) pushdown(st[z--]);
42     while(nroot(x))
43     {
44         y=f[x];z=f[y];
45         if(nroot(y)) rotate( (c[y][0]==x)^(c[z][0]==y) ? x:y );
46         rotate(x);
47     }
48     pushup(x);
49 }
50 inline void access(RI x){//访问
51     for(RI y=0;x;x=f[y=x])
52         splay(x),c[x][1]=y,pushup(x);
53 }
54 inline void makeroot(RI x){//换根
55     access(x);splay(x);
56     pushr(x);
57 }
58 inline int findroot(RI x){//找根（在真实的树中的）
59     access(x);splay(x);
60     while(c[x][0]) pushdown(x),x=c[x][0];
61     return x;
62 }
63 inline void split(RI x,RI y){//提取路径
64     makeroot(x);
65     access(y);splay(y);
66 }
67 inline void link(RI x,RI y){//连边
68     makeroot(x);
69     if(findroot(y)!=x)f[x]=y;
70 }
71 inline void cut(RI x,RI y)//断边
72 {
73     makeroot(x);
74     if(findroot(y)==x&&f[x]==y&&!c[x][1])
75     {
76         f[x]=c[y][0]=0;
77         pushup(y);
78     }
79 }
80 int main()
81 {
82     register char ch;
83     RI n,m,i,type,x,y;
84     n=read();m=read();
85     for(i=1;i<=n;++i){ v[i]=read(); }
86     while(m--)
87     {
88         type=read();x=read();y=read();
89         switch(type)
90         {
91         case 0:split(x,y);printf("%d\n",s[y]);break;
92         case 1:link(x,y);break;
93         case 2:cut(x,y);break;
94         case 3:splay(x);v[x]=y;//先把x转上去再改，不然会影响Splay信息的正确性
95         }
96     }
97     return 0;
98 }
View Code

 

　　

 
posted @ 2018-11-02 00:41  StarHai  阅读(528)  评论(0)  编辑  收藏  举报