HDU 5120 Intersection

Intersection

Time Limit: 4000/4000 MS (Java/Others)    Memory Limit: 512000/512000 K (Java/Others)
Total Submission(s): 4238    Accepted Submission(s): 1623

Problem Description

Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.


A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.


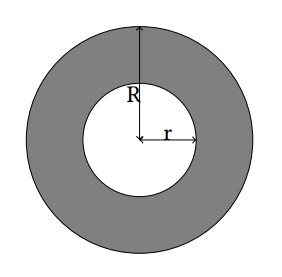
Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

 

 

Input

The first line contains only one integer T (T ≤ 10⁵), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).

Each of the following two lines contains two integers x_i, y_i (0 ≤ x_i, y_i ≤ 20) indicating the coordinates of the center of each ring.

 

 

Output

For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.

 

 

Sample Input

2 2 3 0 0 0 0 2 3 0 0 5 0

 

 

Sample Output

Case #1: 15.707963 Case #2: 2.250778

 

 

Source

2014ACM/ICPC亚洲区北京站-重现赛（感谢北师和上交）

 

 

Recommend

liuyiding

参考代码：

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define rep(i,a,n) for(int i=a;i<n;++i)
#define per(i,a,n) for(int i=n-1;i>=a;--i)
using namespace std;
typedef long long ll;
const double eps = 1e-10;
const double PI = acos(-1.0);
const int maxn = 2500; //注意修改
int n;
//有的命名为sgn函数，高精度符号判断
int dcmp(double x)
{
    //相等函数判断，减少精度问题
    if(fabs(x) < eps) return 0;
    else return x < 0 ? -1 : 1;
}
//点的定义
class Point
{
public:
    double x, y;
    Point(double x = 0, double y = 0): x(x), y(y) {} //构造函数，方便代码的编写
} point[maxn], pafter[maxn];

typedef Point Vector;// 从程序实现上，Vector只是Point的别名

//运算符重载
Vector operator + (const Vector &A, const Vector &B)
{
    return Vector(A.x + B.x, A.y + B.y);    //向量+向量=向量，点+向量=点
}
Vector operator - (const Vector &A, const Vector &B)
{
    return Vector(A.x - B.x, A.y - B.y);    //向量-向量=向量，点-向量-点
}
Vector operator * (const Vector &A, double p)
{
    return Vector(A.x * p, A.y * p);    //向量*数=向量 （数乘）
}
Vector operator / (const Vector &A, double p)
{
    return Vector(A.x / p, A.y / p);    //向量/数=向量 （数除）
}
double operator * (const Vector &A, const Vector &B)
{
    return A.x * B.x + A.y * B.y;    //向量（点乘）向量=数  （点乘）
}
bool operator < (const Point &A, const Point &B)
{
    return A.x == B.x ? A.y < B.y : A.x < B.x;    //按x值递增排序
}
bool operator == (const Point &A, const Point &B)
{
    return dcmp(A.x - B.x) == 0 && dcmp(A.y - B.y) == 0;    //判定两个点是否相同，用到dcmp精度判定
}

//点乘叉乘
double dot(const Vector &A, const Vector &B)
{
    return A.x * B.x + A.y * B.y;    //向量（叉乘）向量=向量 （叉乘）
}
double operator ^ (const Vector &A, const Vector &B)
{
    return A.x * B.y - A.y * B.x;
}
double cross(const Vector &A, const Vector &B)
{
    return A.x * B.y - A.y * B.x;
}

//模长面积
double abs(const Vector &A)
{
    return sqrt(dot(A, A));   //计算向量模长
}
double area2(const Point &A, const Point &B, const Point &C)
{
    return cross(B - A, C - A) ;   //计算平行四边形方向面积
}
double PolygonArea(Point *p, int n)
{
    double area = 0;    //计算多边形的有向面积
    rep(i, 1, n - 1)
    {
        area += cross(p[i] - p[0], p[i + 1] - p[0]);
    }
    return area / 2.0;
}

//旋转
Vector rotate(Vector A, double rad)
{
    return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad));   //旋转rad弧度
}
Vector normal(Vector A)
{
    double l = abs(A);    //计算单位法线，左转90
    return Vector(-A.y / l, A.x / l);
}
double torad(double deg)
{
    return deg / 180 * acos(-1);    //角度转弧度
}

//线段定义
class Line
{
public:
    Point s, e;
    Line() {}
    Line(Point _s, Point _e)
    {
        s = _s;
        e = _e;
    }

} line[maxn];
bool inter(Line l1, Line l2)
{
    return (
               max(l1.s.x, l1.e.x) >= min(l2.s.x, l2.e.x) &&
               max(l2.s.x, l2.e.x) >= min(l1.s.x, l1.e.x) &&
               max(l1.s.y, l1.e.y) >= min(l2.s.y, l2.e.y) &&
               max(l2.s.y, l2.e.y) >= min(l1.s.y, l1.e.y) &&
               dcmp((l2.s - l1.s) ^ (l1.s - l1.e)) * dcmp((l2.e-l1.s) ^ (l1.s - l1.e)) < 0 &&
               dcmp((l1.s - l2.s) ^ (l2.s - l2.e)) * dcmp((l1.e-l2.s) ^ (l2.s - l2.e)) < 0
           ) ;
}

bool inter(Point a1, Point a2, Point b1, Point b2)
{
    Line l1(a1, a2), l2(b1, b2);
    return inter(l1, l2);
}

bool cmp(Point a, Point b)
{
    if(a.x == b.x) return a.y < b.y;
    else return a.x < b.x;
}

double dist(Point a, Point b)
{
    return sqrt((a - b) * (a - b));
}

//求两直线交点
Point getinter(Line l1, Line l2)
{
    Vector v = l1.s - l1.e;
    Vector w = l2.s - l2.e;
    Vector u = l1.e-l2.e;
    double t = cross(w, u) / cross(v, w);
    return l1.e+v * t;
}
Point getinter(Point a1, Point a2, Point b1, Point b2)
{
    Line l1(a1, a2);
    Line l2(b1, b2);
    return getinter(l1, l2);
}
//判定点和线段的关系，
//0:不在线段所在直线上
//1:在线段内（不含端点）
//2:在线段端点
//3:在线段两侧的射线上
int  online(Point a, Line l)
{
    if(dcmp(cross(l.s - a, l.e-a)) != 0) return 0;
    double pans = dcmp(dot(l.s - a, l.e-a));
    if(pans < 0) return 1;
    else if(pans == 0) return 2;
    else if(pans > 0) return 3;
}

int online(Point a, Point b1, Point b2)
{
    Line l(b1, b2);
    return online(a, l);
}

int sgn(double x)
{
    if(fabs(x) < eps) return 0;
    if(x < 0) return -1;
    else return 1;
}

double Area_of_overlap(Point c1, double r1, Point c2, double r2)
{
    double d = dist(c1, c2);
    if(r1 + r2 < d + eps) return 0;
    if(d < fabs(r1 - r2) + eps)
    {
        double r = min(r1, r2);
        return PI * r * r;
    }
    double x = (d * d + r1 * r1 - r2 * r2) / (2 * d);
    double t1 = acos(x / r1);
    double t2 = acos((d - x) / r2);
    return r1 * r1 * t1 + r2 * r2 * t2 - d * r1 * sin(t1);
}

int t;
double RR, rr;
double xx1, yy1, xx2, yy2;
int main()
{
    ios::sync_with_stdio(false);
    cin >> t;
    rep(tt, 1, t + 1)
    {
        cin >> rr >> RR >> xx1 >> yy1 >> xx2 >> yy2;
        double ans1, ans2, ans3, ans4;
        ans1 = Area_of_overlap(Point(xx1, yy1), RR, Point(xx2, yy2), RR);
        ans2 = Area_of_overlap(Point(xx1, yy1), RR, Point(xx2, yy2), rr);
        ans3 = Area_of_overlap(Point(xx1, yy1), rr, Point(xx2, yy2), RR);
        ans4 = Area_of_overlap(Point(xx1, yy1), rr, Point(xx2, yy2), rr);
        cout << "Case #" << tt << ": ";
        cout << fixed << setprecision(6) << ans1 - ans2 - ans3 + ans4 << endl;
    }
    return 0;
}