最短路 & 差分约束 总结
一、引例
1、一类不等式组的解
二、最短路
1、Dijkstra
2、图的存储
3、链式前向星
4、Dijkstra + 优先队列
5、Bellman-Ford
6、SPFA
7、Floyd-Warshall
三、差分约束
1、数形结合
2、三角不等式
3、解的存在性
4、最大值 => 最小值
5、不等式标准化
四、差分约束的经典应用
1、线性约束
2、区间约束
3、未知条件约束
五、最短路的代码模版
1.Dijkstra a.邻接矩阵实现,b.优先队列优化实现
2.Bellman-Ford
3.SPFA(FIFO队列优化)
4.Folyd
一、引例
1、一类不等式组的解
给定n个变量和m个不等式,每个不等式形如 x[i] - x[j] <= a[k] (0 <= i, j < n, 0 <= k < m, a[k]已知),求 x[n-1] - x[0] 的最大值。例如当n = 4,m = 5,不等式组如图一-1-1所示的情况,求x3 - x0的最大值。
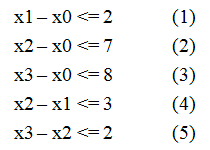
图一-1-1
观察x3 - x0的性质,我们如果可以通过不等式的两两加和得到c个形如 x3 - x0 <= Ti 的不等式,那么 min{ Ti | 0 <= i < c } 就是我们要求的x3 - x0的最大值。于是开始人肉,费尽千辛万苦,终于整理出以下三个不等式:
1. (3) x3 - x0 <= 8
2. (2) + (5) x3 - x0 <= 9
3. (1) + (4) + (5) x3 - x0 <= 7
这里的T等于{8, 9, 7},所以min{ T } = 7,答案就是7。的确是7吗?我们再仔细看看,发现的确没有其它情况了。那么问题就是这种方法即使做出来了还是带有问号的,不能确定正确与否,如何系统地解决这类问题呢?
让我们来看另一个问题,这个问题描述相对简单,给定四个小岛以及小岛之间的有向距离,问从第0个岛到第3个岛的最短距离。如图一-1-2所示,箭头指向的线段代表两个小岛之间的有向边,蓝色数字代表距离权值。
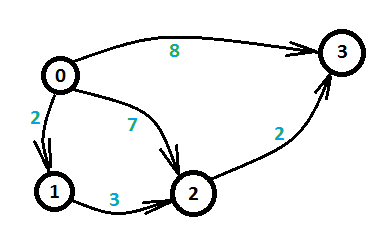
图一-1-2
这个问题就是经典的最短路问题。由于这个图比较简单,我们可以枚举所有的路线,发现总共三条路线,如下:
1. 0 -> 3 长度为8
2. 0 -> 2 -> 3 长度为7+2 = 9
3. 0 -> 1 -> 2 -> 3 长度为2 + 3 + 2 = 7
最短路为三条线路中的长度的最小值即7,所以最短路的长度就是7。这和上面的不等式有什么关系呢?还是先来看看最短路求解的原理,看懂原理自然就能想到两者的联系了。
二、最短路
1、Dijkstra
对于一个有向图或无向图,所有边权为正(边用邻接矩阵的形式给出),给定a和b,求a到b的最短路,保证a一定能够到达b。这条最短路是否一定存在呢?答案是肯定的。相反,最长路就不一定了,由于边权为正,如果遇到有环的时候,可以一直在这个环上走,因为要找最长的,这样就使得路径越变越长,永无止境,所以对于正权图,在可达的情况下最短路一定存在,最长路则不一定存在。这里先讨论正权图的最短路问题。
最短路满足最优子结构性质,所以是一个动态规划问题。最短路的最优子结构可以描述为:
D(s, t) = {Vs ... Vi ... Vj ... Vt}表示s到t的最短路,其中i和j是这条路径上的两个中间结点,那么D(i, j)必定是i到j的最短路,这个性质是显然的,可以用反证法证明。
基于上面的最优子结构性质,如果存在这样一条最短路D(s, t) = {Vs ... Vi Vt},其中i和t是最短路上相邻的点,那么D(s, i) = {Vs ... Vi} 必定是s到i的最短路。Dijkstra算法就是基于这样一个性质,通过最短路径长度递增,逐渐生成最短路。
Dijkstra算法是最经典的最短路算法,用于计算正权图的单源最短路(Single Source Shortest Path,源点给定,通过该算法可以求出起点到所有点的最短路),它是基于这样一个事实:如果源点到x点的最短路已经求出,并且保存在d[x] ( 可以将它理解为D(s, x) )上,那么可以利用x去更新 x能够直接到达的点 的最短路。即:
d[y] = min{ d[y], d[x] + w(x, y) } y为x能够直接到达的点,w(x, y) 则表示x->y这条有向边的边权
具体算法描述如下:对于图G = <V, E>,源点为s,d[i]表示s到i的最短路,visit[i]表示d[i]是否已经确定(布尔值)。
1) 初始化 所有顶点 d[i] = INF, visit[i] = false,令d[s] = 0;
2) 从所有visit[i]为false的顶点中找到一个d[i]值最小的,令x = i; 如果找不到,算法结束;
3) 标记visit[x] = true, 更新和x直接相邻的所有顶点y的最短路: d[y] = min{ d[y], d[x] + w(x, y) }
(第三步中如果y和x并不是直接相邻,则令w(x, y) = INF)
2、图的存储
以上算法的时间复杂度为O(n^2),n为结点个数,即每次找一个d[i]值最小的,总共n次,每次找到后对其它所有顶点进行更新,更新n次。由于算法复杂度是和点有关,并且平方级别的,所以还是需要考虑一下点数较多而边数较少的情况,接下来以图一-2-1为例讨论一下边的存储方式。
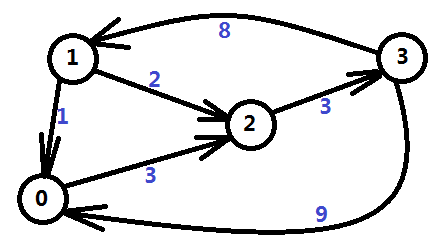
图一-2-1
邻接矩阵是直接利用一个二维数组对边的关系进行存储,矩阵的第i行第j列的值 表示 i -> j 这条边的权值;特殊的,如果不存在这条边,用一个特殊标记来表示;如果i == j,则权值为0。它的优点是实现非常简单,而且很容易理解;缺点也很明显,如果这个图是一个非常稀疏的图,图中边很少,但是点很多,就会造成非常大的内存浪费,点数过大的时候根本就无法存储。图一-2-2展示了图一-2-1的邻接矩阵表示法。
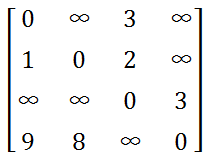
图一-2-2
邻接表是图中常用的存储结构之一,每个顶点都有一个链表,这个链表的数据表示和当前顶点直接相邻的顶点(如果边有权值,还需要保存边权信息)。邻接表的优点是对于稀疏图不会有数据浪费,缺点就是实现相对麻烦,需要自己实现链表,动态分配内存。图一-2-3展示了图一-2-1的邻接表表示法。

图一-2-3
前向星是以存储边的方式来存储图,先将边读入并存储在连续的数组中,然后按照边的起点进行排序,这样数组中起点相等的边就能够在数组中进行连续访问了。它的优点是实现简单,容易理解,缺点是需要在所有边都读入完毕的情况下对所有边进行一次排序,带来了时间开销,实用性也较差,只适合离线算法。图一-2-4展示了图一-2-1的前向星表示法。
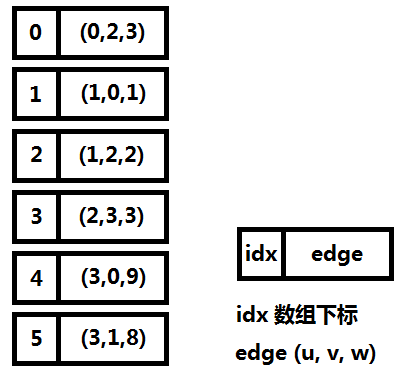
图二-2-4
那么用哪种数据结构才能满足所有图的需求呢?这里介绍一种新的数据结构一一链式前向星。
3、链式前向星
链式前向星和邻接表类似,也是链式结构和线性结构的结合,每个结点i都有一个链表,链表的所有数据是从i出发的所有边的集合(对比邻接表存的是顶点集合),边的表示为一个四元组(u, v, w, next),其中(u, v)代表该条边的有向顶点对,w代表边上的权值,next指向下一条边。
具体的,我们需要一个边的结构体数组 edge[MAXM],MAXM表示边的总数,所有边都存储在这个结构体数组中,并且用head[i]来指向 i 结点的第一条边。
边的结构体声明如下:
struct EDGE {
int u, v, w, next;
EDGE() {}
EDGE(int _u, int _v, int _w, int _next) {
u = _u, v = _v, w = _w, next = _next;
}
}edge[MAXM];
初始化所有的head[i] = INF,当前边总数 edgeCount = 0
每读入一条边,调用addEdge(u, v, w),具体函数的实现如下:
void addEdge(int u, int v, int w) {
edge[ edgeCount ] = EDGE(u, v, w, head[u]);
head[u] = edgeCount ++;
}
这个函数的含义是每加入一条边(u, v),就在原有的链表结构的首部插入这条边,使得每次插入的时间复杂度为O(1),所以链表的边的顺序和读入顺序正好是逆序的。这种结构在无论是稠密的还是稀疏的图上都有非常好的表现,空间上没有浪费,时间上也是最小开销。
调用的时候只要通过head[i]就能访问到由 i 出发的第一条边的编号,通过编号到edge数组进行索引可以得到边的具体信息,然后根据这条边的next域可以得到第二条边的编号,以此类推,直到next域为INF(这里的INF即head数组初始化的那个值,一般取-1即可)。
4、Dijkstra + 优先队列(小顶堆)
有了链式前向星,再来看Dijkstra算法,我们关注算法的第3)步,对和x直接相邻的点进行更新的时候,不再需要遍历所有的点,而是只更新和x直接相邻的点,这样总的更新次数就和顶点数n无关了,总更新次数就是总边数m,算法的复杂度变成了O(n^2 + m),之前的复杂度是O(n^2),但是有两个n^2的操作,而这里是一个,原因在于找d值最小的顶点的时候还是一个O(n)的轮询,总共n次查找。那么查找d值最小有什么好办法呢?
数据结构中有一种树,它能够在O( log(n) )的时间内插入和删除数据,并且在O(1)的时间内得到当前数据的最小值,这个和我们的需求不谋而合,它就是最小二叉堆(小顶堆),具体实现不讲了,比较简单,可以自行百度。
在C++中,可以利用STL的优先队列( priority_queue )来实现获取最小值的操作,这里直接给出利用优先队列优化的Dijkstra算法的类C++伪代码(请勿直接复制粘贴到C++编译器中编译执行),然后再进行讨论:
void Dijkstra_Heap(s) {
for(i = 0; i < n; i++) {
d[i] = (i == s) ? 0 : INF; // 注释1
}
q.push( (d[s], s) ); // 注释2
while( !q.empty() ) {
(dist, u) = q.top(); // 注释3
q.pop(); // 注释4
for (e = head[u]; e != INF; e = edge[e].next) {
v = edge[e].v;
w = edge[e].w;
if(d[u] + w < d[v]) {
d[v] = d[u] + w;
path[v] = u;
q.push( (d[v], v) );
}
}
}
}
注释1:初始化s到i的初始最短距离,d[s] = 0
注释2:q即优先队列,这里略去声明是为了将代码简化,让读者能够关注算法本身而不是关注具体实现, push是执行优先队列的插入操作,插入的数据为一个二元组(d[u], u)
注释3:执行优先队列的获取操作,获取的二元组为当前队列中d值最小的
注释4:执行优先队列的删除操作,删除队列顶部的元素(即注释3中d值最小的那个二元组)
以上伪代码中的主体部分竟然没有任何注释,这是因为我要用黑色的字来描述它的重要性,而注释只是注释一些和语法相关的内容。
主体代码只有一个循环,这个循环就是遍历了u这个结点的边链表,其中e为边编号,edge[e].w即上文提到的w(u, v),即u ->v 这条边的权值,而d[u] + w(u, v) < d[v]表示从起点s到u,再经过(u, v)这条边到达v的最短路比之前其它方式到达v的最短路还短,如图二-4-1所示,如果满足这个条件,那么就更新这条最短路,并且利用path数组来记录最短路中每个结点的前驱结点,path[v] = u,表示到达v的最短路的前驱结点为u。
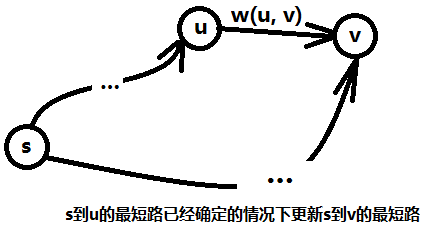
图二-4-1
补充一点,这个算法求出的是一棵最短路径树,其中s为根结点,结点之间的关系是通过path数组来建立的,path[v] = u,表明u为v的父结点(树的存储不一定要存儿子结点,也可以用存父结点的方式表示)。
考虑这个算法的复杂度,如果用n表示点数,m表示边数,那么优先队列中最多可能存在的点数有多少?因为我们在把顶点插入队列的时候并没有判断队列中有没有这个点,而且也不能进行这样的判断,因为新插入的点一定会取代之前的点(距离更短才会执行插入),所以同一时间队列中的点有可能重复,插入操作的上限是m次,所以最多有m个点,那么一次插入和删除的操作的平摊复杂度就是O(logm),但是每次取距离最小的点,对于有多个相同点的情况,如果那个点已经出过一次队列了,下次同一个点出队列的时候它对应的距离一定比之前的大,不需要用它去更新其它点,因为一定不可能更新成功,所以真正执行更新操作的点的个数其实只有n个,所以总体下来的平均复杂度为O( (m+n)log m),而这个只是理论上界,一般问题中都是很快就能找到最短路的,所以实际复杂度会比这个小很多,相比O(n^2)的算法已经优化了很多了。
Dijkstra算法求的是正权图的单源最短路问题,对于权值有负数的情况就不能用Dijkstra求解了,因为如果图中存在负环,Dijkstra带优先队列优化的算法就会进入一个死循环,因为可以从起点走到负环处一直将权值变小 。对于带负权的图的最短路问题就需要用到Bellman-Ford算法了。
5、Bellman-Ford
Bellman-Ford算法可以在最短路存在的情况下求出最短路,并且在存在负权圈的情况下告诉你最短路不存在,前提是起点能够到达这个负权圈,因为即使图中有负权圈,但是起点到不了负权圈,最短路还是有可能存在的。它是基于这样一个事实:一个图的最短路如果存在,那么最短路中必定不存在圈,所以最短路的顶点数除了起点外最多只有n-1个。
Bellman-Ford同样也是利用了最短路的最优子结构性质,用d[i]表示起点s到i的最短路,那么边数上限为 j 的最短路可以通过边数上限为 j-1 的最短路 加入一条边 得到,通过n-1次迭代,最后求得s到所有点的最短路。
具体算法描述如下:对于图G = <V, E>,源点为s,d[i]表示s到i的最短路。
1) 初始化 所有顶点 d[i] = INF, 令d[s] = 0,计数器 j = 0;
2) 枚举每条边(u, v),如果d[u]不等于INF并且 d[u] + w(u, v) < d[v],则令d[v] = d[u] + w(u, v);
3) 计数器j + +,当j = n - 1时算法结束,否则继续重复2)的步骤;
第2)步的一次更新称为边的“松弛”操作。
以上算法并没有考虑到负权圈的问题,如果存在负圈权,那么第2)步操作的更新会永无止境,所以判定负权圈的算法也就出来了,只需要在第n次继续进行第2)步的松弛操作,如果有至少一条边能够被更新,那么必定存在负权圈。
这个算法的时间复杂度为O(nm),n为点数,m为边数。
这里有一个小优化,我们可以注意到第2)步操作,每次迭代第2)步操作都是做同一件事情,也就是说如果第k(k <= n-1)次迭代的时候没有任何的最短路发生更新,即所有的d[i]值都未发生变化,那么第k+1次必定也不会发生变化了,也就是说这个算法提前结束了。所以可以在第2)操作开始的时候记录一个标志,标志初始为false,如果有一条边发生了松弛,那么标志置为true,所有边枚举完毕如果标志还是false则提前结束算法。
这个优化在一般情况下很有效,因为往往最短路在前几次迭代就已经找到最优解了,但是也不排除上文提到的负权圈的情况,会一直更新,使得整个算法的时间复杂度达到上限O(nm),那么如何改善这个算法的效率呢?接下来介绍改进版的Bellman-Ford 一一 SPFA。
6、SPFA
SPFA( Shortest Path Faster Algorithm )是基于Bellman-Ford的思想,采用先进先出(FIFO)队列进行优化的一个计算单源最短路的快速算法。
类似Bellman-Ford的做法,我们用数组d记录每个结点的最短路径估计值,并用链式前向星来存储图G。利用一个先进先出的队列用来保存待松弛的结点,每次取出队首结点u,并且枚举从u出发的所有边(u, v),如果d[u] + w(u, v) < d[v],则更新d[v] = d[u] + w(u, v),然后判断v点在不在队列中,如果不在就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
只要最短路径存在,SPFA算法必定能求出最小值。因为每次将点放入队尾,都是经过松弛操作达到的。即每次入队的点v对应的最短路径估计值d[v]都在变小。所以算法的执行会使d越来越小。由于我们假定最短路一定存在,即图中没有负权圈,所以每个结点都有最短路径值。因此,算法不会无限执行下去,随着d值的逐渐变小,直到到达最短路径值时,算法结束,这时的最短路径估计值就是对应结点的最短路径值。
那么最短路径不存在呢?如果存在负权圈,并且起点可以通过一些顶点到达负权圈,那么利用SPFA算法会进入一个死循环,因为d值会越来越小,并且没有下限,使得最短路不存在。那么我们假设不存在负权圈,则任何最短路上的点必定小于等于n个(没有圈),换言之,用一个数组c[i]来记录i这个点入队的次数,所有的c[i]必定都小于等于n,所以一旦有一个c[i] > n,则表明这个图中存在负权圈。
接下来给出SPFA更加直观的理解,假设图中所有边的边权都为1,那么SPFA其实就是一个BFS(Breadth First Search,广度优先搜索),对于BFS的介绍可以参阅搜索入门。BFS首先到达的顶点所经历的路径一定是最短路(也就是经过的最少顶点数),所以此时利用数组记录节点访问可以使每个顶点只进队一次,但在至少有一条边的边权不为1的带权图中,最先到达的顶点的路径不一定是最短路,这就是为什么要用d数组来记录当前最短路估计值的原因了。
最后给出SPFA的类C++伪代码(请勿直接复制粘贴到C++编译器中编译执行):
bool spfa(s) {
for(i = 0; i < n; i++) {
d[i] = (i == s) ? 0 : INF;
inq[i] = (i == s); // 注释1
visitCount[i] = 0;
}
q.push( (d[s], s) );
while( !q.empty() ) {
(dist, u) = q.front(); // 注释2
q.pop();
inq[u] = false;
if( visitCount[u]++ > n ) { // 注释3
return true;
}
for (e = head[u]; e != INF; e = edge[e].next) {
v = edge[e].v;
w = edge[e].w;
if(d[u] + w < d[v]) { // 注释4
d[v] = d[u] + w;
if ( !inq[v] ) {
inq[v] = true;
q.push( (d[v], v) );
}
}
}
}
return false;
}
注释1:inq[i]表示结点i是否在队列中,初始时只有s在队列中;
注释2:q.front()为FIFO队列的队列首元素;
注释3:判断是否存在负权圈,如果存在,函数返回true;
注释4:和Dijkstra优先队列优化的算法很相似的松弛操作;
以上伪代码实现的SPFA算法的最坏时间复杂度为O(nm),其中n为点数,m为边数,但是一般不会达到这个上界,一般的期望时间复杂度为O(km), k为常数,m为边数(这个时间复杂度只是估计值,具体和图的结构有很大关系,而且很难证明,不过可以肯定的是至少比传统的Bellman-Ford高效很多,所以一般采用SPFA来求解带负权圈的最短路问题)。
7、Floyd-Warshall
最后介绍一个求任意两点最短路的算法,很显然,我们可以求n次单源最短路(枚举起点),但是下面这种方法更加容易编码,而且很巧妙,它也是基于动态规划的思想。
令d[i][j][k]为只允许经过结点[0, k]的情况下,i 到 j的最短路。那么利用最优子结构性质,有两种情况:
a. 如果最短路经过k点,则d[i][j][k] = d[i][k][k-1] + d[k][j][k-1];
b. 如果最短路不经过k点,则d[i][j][k] = d[i][j][k-1];
于是有状态转移方程: d[i][j][k] = min{ d[i][j][k-1], d[i][k][k-1] + d[k][j][k-1] } (0 <= i, j, k < n)
这是一个3D/0D问题,只需要按照k递增的顺序进行枚举,就能在O(n^3)的时间内求解,又第三维的状态可以采用滚动数组进行优化,所以空间复杂度为O(n^2)。
三、差分约束
1、数形结合
介绍完最短路,回到之前提到的那个不等式组的问题上来,我们将它更加系统化。
如若一个系统由n个变量和m个不等式组成,并且这m个不等式对应的系数矩阵中每一行有且仅有一个1和-1,其它的都为0,这样的系统称为差分约束( difference constraints )系统。引例中的不等式组可以表示成如图三-1-1的系数矩阵。
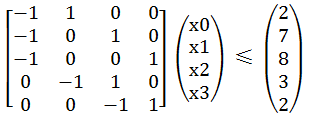
图三-1-1
然后继续回到单个不等式上来,观察 x[i] - x[j] <= a[k], 将这个不等式稍稍变形,将x[j]移到不等式右边,则有x[i] <= x[j] + a[k],然后我们令a[k] = w(j, i),再将不等式中的i和j变量替换掉,i = v, j = u,将x数组的名字改成d(以上都是等价变换,不会改变原有不等式的性质),则原先的不等式变成了以下形式:d[u] + w(u, v) >= d[v]。
这时候联想到SPFA中的一个松弛操作:
if(d[u] + w(u, v) < d[v]) {
d[v] = d[u] + w(u, v);
}
对比上面的不等式,两个不等式的不等号正好相反,但是再仔细一想,其实它们的逻辑是一致的,因为SPFA的松弛操作是在满足小于的情况下进行松弛,力求达到d[u] + w(u, v) >= d[v],而我们之前令a[k] = w(j, i),所以我们可以将每个不等式转化成图上的有向边:
对于每个不等式 x[i] - x[j] <= a[k],对结点 j 和 i 建立一条 j -> i的有向边,边权为a[k],求x[n-1] - x[0] 的最大值就是求 0 到n-1的最短路。
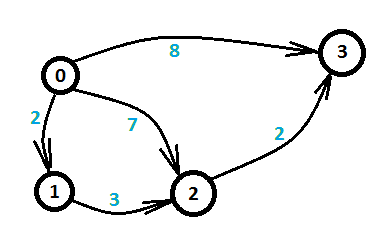
图三-1-2
图三-1-2 展示了 图三-1-1的不等式组转化后的图。
2、三角不等式
如果还没有完全理解,我们可以先来看一个简单的情况,如下三个不等式:
B - A <= c (1)
C - B <= a (2)
C - A <= b (3)
我们想要知道C - A的最大值,通过(1) + (2),可以得到 C - A <= a + c,所以这个问题其实就是求min{b, a+c}。将上面的三个不等式按照 三-1 数形结合 中提到的方式建图,如图三-2-1所示。
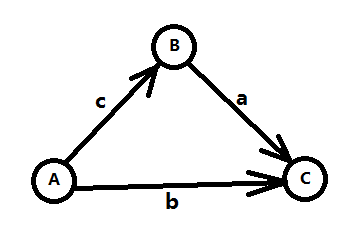
图三-2-1
我们发现min{b, a+c}正好对应了A到C的最短路,而这三个不等式就是著名的三角不等式。将三个不等式推广到m个,变量推广到n个,就变成了n个点m条边的最短路问题了。
3、解的存在性
上文提到最短路的时候,会出现负权圈或者根本就不可达的情况,所以在不等式组转化的图上也有可能出现上述情况,先来看负权圈的情况,如图三-3-1,下图为5个变量5个不等式转化后的图,需要求得是X[t] - X[s]的最大值,可以转化成求s到t的最短路,但是路径中出现负权圈,则表示最短路无限小,即不存在最短路,那么在不等式上的表现即X[t] - X[s] <= T中的T无限小,得出的结论就是 X[t] - X[s]的最大值 不存在。
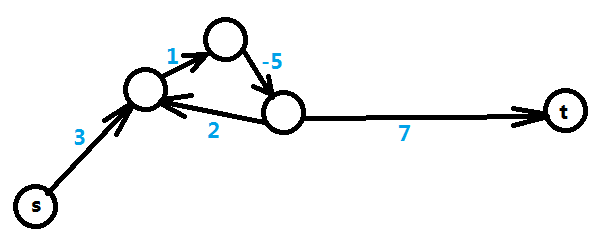
图三-3-1
再来看另一种情况,即从起点s无法到达t的情况,如图三-3-2,表明X[t]和X[s]之间并没有约束关系,这种情况下X[t] - X[s]的最大值是无限大,这就表明了X[t]和X[s]的取值有无限多种。
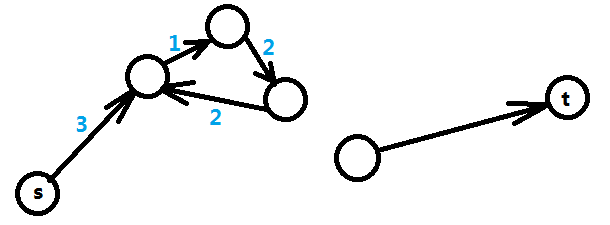
图三-3-2
在实际问题中这两种情况会让你给出不同的输出。综上所述,差分约束系统的解有三种情况:1、有解;2、无解;3、无限多解;
4、最大值 => 最小值
然后,我们将问题进行一个简单的转化,将原先的"<="变成">=",转化后的不等式如下:
B - A >= c (1)
C - B >= a (2)
C - A >= b (3)
然后求C - A的最小值,类比之前的方法,需要求的其实是max{b, c+a},于是对应的是图三-2-1从A到C的最长路。同样可以推广到n个变量m个不等式的情况。
5、不等式标准化
如果给出的不等式有"<="也有">=",又该如何解决呢?很明显,首先需要关注最后的问题是什么,如果需要求的是两个变量差的最大值,那么需要将所有不等式转变成"<="的形式,建图后求最短路;相反,如果需要求的是两个变量差的最小值,那么需要将所有不等式转化成">=",建图后求最长路。
如果有形如:A - B = c 这样的等式呢?我们可以将它转化成以下两个不等式:
A - B >= c (1)
A - B <= c (2)
再通过上面的方法将其中一种不等号反向,建图即可。
最后,如果这些变量都是整数域上的,那么遇到A - B < c这样的不带等号的不等式,我们需要将它转化成"<="或者">="的形式,即 A - B <= c - 1。
四、差分约束的经典应用
1、线性约束
线性约束一般是在一维空间中给出一些变量(一般定义位置),然后告诉你某两个变量的约束关系,求两个变量a和b的差值的最大值或最小值。
【例题1】N个人编号为1-N,并且按照编号顺序排成一条直线,任何两个人的位置不重合,然后给定一些约束条件。
X(X <= 100000)组约束Ax Bx Cx(1 <= Ax < Bx <= N),表示Ax和Bx的距离不能大于Cx。
Y(X <= 100000)组约束Ay By Cy(1 <= Ay < By <= N),表示Ay和By的距离不能小于Cy。
如果这样的排列存在,输出1-N这两个人的最长可能距离,如果不存在,输出-1,如果无限长输出-2。
像这类问题,N个人的位置在一条直线上呈线性排列,某两个人的位置满足某些约束条件,最后要求第一个人和最后一个人的最长可能距离,这种是最直白的差分约束问题,因为可以用距离作为变量列出不等式组,然后再转化成图求最短路。
令第x个人的位置为d[x](不妨设d[x]为x的递增函数,即随着x的增大,d[x]的位置朝着x正方向延伸)。
那么我们可以列出一些约束条件如下:
1、对于所有的Ax Bx Cx,有 d[Bx] - d[Ax] <= Cx;
2、对于所有的Ay By Cy,有 d[By] - d[Ay] >= Cy;
3、然后根据我们的设定,有 d[x] >= d[x-1] + 1 (1 < x <= N) (这个条件是表示任何两个人的位置不重合)
而我们需要求的是d[N] - d[1]的最大值,即表示成d[N] - d[1] <= T,要求的就是这个T。
于是我们将所有的不等式都转化成d[x] - d[y] <= z的形式,如下:
1、d[Bx] - d[Ax] <= Cx
2、d[Ay] - d[By] <= -Cy
3、d[x-1] - d[x] <= -1
对于d[x] - d[y] <= z,令z = w(y, x),那么有 d[x] <= d[y] + w(y, x),所以当d[x] > d[y] + w(y, x),我们需要更新d[x]的值,这对应了最短路的松弛操作,于是问题转化成了求1到N的最短路。
对于所有满足d[x] - d[y] <= z的不等式,从y向x建立一条权值为z的有向边。
然后从起点1出发,利用SPFA求到各个点的最短路,如果1到N不可达,说明最短路(即上文中的T)无限长,输出-2。如果某个点进入队列大于等于N次,则必定存在一条负环,即没有最短路,输出-1。否则T就等于1到N的最短路。
2、区间约束
【例题2】给定n(n <= 50000)个整点闭区间和这个区间中至少有多少整点需要被选中,每个区间的范围为[ai, bi],并且至少有ci个点需要被选中,其中0 <= ai <= bi <= 50000,问[0, 50000]至少需要有多少点被选中。
例如3 6 2 表示[3, 6]这个区间至少需要选择2个点,可以是3,4也可以是4,6(总情况有 C(4, 2)种 )。
这类问题就没有线性约束那么明显,需要将问题进行一下转化,考虑到最后需要求的是一个完整区间内至少有多少点被选中,试着用d[i]表示[0, i]这个区间至少有多少点能被选中,根据定义,可以抽象出 d[-1] = 0,对于每个区间描述,可以表示成d[ bi ] - d[ ai - 1 ] >= ci,而我们的目标要求的是 d[ 50000 ] - d[ -1 ] >= T 这个不等式中的T,将所有区间描述转化成图后求-1到50000的最长路。
这里忽略了一些要素,因为d[i]描述了一个求和函数,所以对于d[i]和d[i-1]其实是有自身限制的,考虑到每个点有选和不选两种状态,所以d[i]和d[i-1]需要满足以下不等式: 0 <= d[i] - d[i-1] <= 1 (即第i个数选还是不选)
这样一来,还需要加入 50000*2 = 100000 条边,由于边数和点数都是万级别的,所以不能采用单纯的Bellman-Ford ,需要利用SPFA进行优化,由于-1不能映射到小标,所以可以将所有点都向x轴正方向偏移1个单位(即所有数+1)。
3、未知条件约束
未知条件约束是指在不等式的右边不一定是个常数,可能是个未知数,可以通过枚举这个未知数,然后对不等式转化成差分约束进行求解。
【例题3】
在一家超市里,每个时刻都需要有营业员看管,R(i) (0 <= i < 24)表示从i时刻开始到i+1时刻结束需要的营业员的数目,现在有N(N <= 1000)个申请人申请这项工作,并且每个申请者都有一个起始工作时间 ti,如果第i个申请者被录用,那么他会连续工作8小时。
现在要求选择一些申请者进行录用,使得任何一个时刻i,营业员数目都能大于等于R(i)。
i = 0 1 2 3 4 5 6 ... 20 21 22 23 23,分别对应时刻 [i, i+1),特殊的,23表示的是[23, 0),并且有些申请者的工作时间可能会“跨天”。
a[i] 表示在第i时刻开始工作的人数,是个未知量
b[i] 表示在第i时刻能够开始工作人数的上限, 是个已知量
R[i] 表示在第i时刻必须值班的人数,也是已知量
那么第i时刻到第i+1时刻还在工作的人满足下面两个不等式(利用每人工作时间8小时这个条件):
当 i >= 7, a[i-7] + a[i-6] + ... + a[i] >= R[i] (1)
当 0 <= i < 7, (a[0] + ... + a[i]) + (a[i+17] + ... + a[23]) >= R[i] (2)
对于从第i时刻开始工作的人,满足以下不等式:
0 <= i < 24, 0 <= a[i] <= b[i] (3)
令 s[i] = a[0] + ... + a[i],特殊地,s[-1] = 0
上面三个式子用s[i]来表示,如下:
s[i] - s[i-8] >= R[i] (i >= 7) (1)
s[i] + s[23] - s[i+16] >= R[i] (0 <= i < 7) (2)
0 <= s[i] - s[i-1] <= b[i] (0 <= i < 24) (3)
仔细观察不等式(2),有三个未知数,这里的s[23]就是未知条件,所以还无法转化成差分约束求解,但是和i相关的变量只有两个,对于s[23]的值我们可以进行枚举,令s[23] = T, 则有以下几个不等式:
s[i] - s[i-8] >= R[i]
s[i] - s[i+16] >= R[i] - T
s[i] - s[i-1] >= 0
s[i-1] - s[i] >= -b[i]
对于所有的不等式 s[y] - s[x] >= c,建立一条权值为c的边 x->y,于是问题转化成了求从原点-1到终点23的最长路。
但是这个问题比较特殊,我们还少了一个条件,即:s[23] = T,它并不是一个不等式,我们需要将它也转化成不等式,由于设定s[-1] = 0,所以 s[23] - s[-1] = T,它可以转化成两个不等式:
s[23] - s[-1] >= T
s[-1] - s[23] >= -T
将这两条边补到原图中,求出的最长路s[23]等于T,表示T就是满足条件的一个解,由于T的值时从小到大枚举的(T的范围为0到N),所以第一个满足条件的解就是答案。
最后,观察申请者的数量,当i个申请者能够满足条件的时候,i+1个申请者必定可以满足条件,所以申请者的数量是满足单调性的,可以对T进行二分枚举,将枚举复杂度从O(N)降为O(logN)。
五、最短路的代码模版
1.Dijkstra
a.邻接矩阵实现(核心代码)
//dis存贮权值 vis是否执行过 mpa用邻接矩阵存贮
void dijkstra(int s)
{
int min_dis,u; //初始化dis为v行的权值,vis为0
memset(dis,MAX,sizeof(dis));
for(int i=1;i<=n;i++)
{
dis[i]=mpa[s][i];
vis[i]=0;
}
vis[s]=1; //标记第一个v走过
for(int i=1;i<n;i++)//一共需要执行n-1轮
{
min_dis=MAX;
u=-1;
for(int j=1;j<=n;j++)
{
if(!vis[j] && dis[j]<min_dis)
{
u=j;
min_dis=dis[j];
}
}//寻找当前没有走过dis值最小的标号 if(u==-1) break;没有与之相连的点
vis[u]=1;//标记u走过
for(int j=1; j<=n; j++)
if(!vis[j]) dis[j]=min(dis[u]+mpa[u][j],dis[j]);
//比较当前dis[u]+mpa[u][j]是否小于dis[j],取每次的最小
}
}
b.优先队列优化实现(核心代码)
struct Edge{
int u,v,w;
Edge(int uu,int vv,int ww):u(uu),v(vv),w(ww){ }
};
vector<Edge> edge[maxn];
struct Node{
int Id,W;
bool operator < (const Node &b) const { W>b.W;}
};
void addedge(int u,int v,int w)
{
edge[u].push_back(Edge(u,v,w));
}
void Dijkstra(int s)
{
memset(vis,0,sizeof vis); memset(dis,INF,sizeof dis);
priority_queue<Node> q;
q.push(Node{s,0}),dis[s]=0;
while(!q.empty())
{
Node u=q.top();q.pop();
int id=u.Id;
if(vis[id]) continue;
vis[id]=1;
for(int i=0;i<edge[id].size();i++)
{
if(!vis[edge[id][i].v] && dis[edge[id][i].v]>dis[id]+edge[id][i].w)
{
dis[edge[id][i].v]=dis[id]+edge[id][i].w;
q.push(Node{edge[id][i].v,dis[edge[id][i].v]});
}
}
}
}
2.Bellman-Ford (核心代码)
const int maxn=10010;
const int INF=0x3f3f3f3f;
int n,m,dis[1010];
struct Edge{
int u,v,w;
} edge[maxn<<1];
int main()
{
while(cin>>n>>m,n+m)
{
for(int i=1;i<=2*m;i+=2)
{
cin>>edge[i].u>>edge[i].v>>edge[i].w;
edge[i+1].u=edge[i].v,edge[i+1].v=edge[i].u,edge[i+1].w=edge[i].w;//无向图
}
for(int i=1;i<=n;i++) dis[i]=INF;dis[1]=0;
for(int k=1;k<n;k++)
{
for(int i=1;i<=2*m;i++)
{
if(dis[edge[i].u]<INF)
dis[edge[i].v]=min(dis[edge[i].v],dis[edge[i].u]+edge[i].w);
}
}
/* //判断是否含有负权回路
bool flag=false;
for(int i=1;i<=2*m;i++)
{
if(dis[edge[i].v]>dis[edge[i].u]+edge[i].w)
{
flag=true; break;
}
}
if(flag) cout<<"Orz,此图含有负权回路"<<endl;
*/
cout<<dis[n]<<endl;
}
return 0;
}3.SPFA(FIFO队列优化)(核心代码)
const int maxn=10010;
const int INF=0x3f3f3f3f;
struct Edge{
int u,v,w;
Edge(int from,int to,int ww) : u(from),v(to),w(ww) { }
};
vector<Edge> edges;
vector<int> G[1010];
int n,m,u,v,w,vis[maxn<<1],dis[1010],cnt[maxn<<1];
void Init()
{
memset(dis,INF,sizeof dis);dis[1]=0;
memset(vis,0,sizeof vis);
memset(cnt,0,sizeof cnt);
for(int i=0;i<1010;i++) G[i].clear();
edges.clear();
}
void addedge(int u,int v,int w)
{
edges.push_back(Edge(u,v,w));
G[u].push_back(edges.size()-1);
}
bool SPFA(int s)
{
queue<int> q;
q.push(s);
vis[s]=1;
while(!q.empty())
{
int u=q.front();q.pop();
vis[u]=0;
for(int i=0;i<G[u].size();i++)
{
if(dis[u]<INF && dis[edges[G[u][i]].v]>dis[u]+edges[G[u][i]].w)
{
dis[edges[G[u][i]].v]=dis[u]+edges[G[u][i]].w;
if(!vis[edges[G[u][i]].v]){
q.push(edges[G[u][i]].v);vis[edges[G[u][i]].v]=1;
if(++cnt[edges[G[u][i]].v]>n) return false;//Orz有负权回路
}
}
}
}
return true;
}4.Folyd(核心代码)
int n,m,u,v,w;
cin>>n>>m;
vector<vector<int> > dis[n];
for(int i=0;i<n;i++) dis[i].resize(n,INF),dis[i][i]=0;
for(int i=0;i<m;i++)
{
cin>>u>>v>>w;
dis[u][v]=w;
//dis[v][u]=w;无向图
}
//核心
for(int k=0;k<n;k++)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
dis[i][j]=min(dis[i][k],dis[k][j]);
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号