leetcode字节跳动专题（35题）

挑战字符串

 无重复字符的最长子串

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

题解：

利用set的无重复性。我们记录两个指针l和r,分别表示左右边界，移动r指针，如果在set集合里面出现了s[r],则移动左指针，直到set里面没有s[r],重复上诉步骤；

参考代码:

 1 class Solution {
 2 public:
 3     int lengthOfLongestSubstring(string s) {
 4         set<char> st;
 5         int l=0,r=0,ans=0;
 6         while(r<s.size())
 7         {
 8             if(!st.count(s[r]))
 9             {
10                 st.insert(s[r]);
11                 ans=max(ans,(int)st.size());
12                 r++;
13             }
14             else st.erase(s[l++]);
15         }
16         return ans;  
17     }
18 };
C++

最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1:

输入: ["flower","flow","flight"]
输出: "fl"

示例 2:

输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。

说明:

所有输入只包含小写字母 a-z 。

题解：就是按照题意匹配就行了.(O(n^2))

参考代码：

 1 class Solution {
 2 public:
 3     string longestCommonPrefix(vector<string>& strs) {
 4         string ans;
 5         if(strs.empty())
 6             return ans;
 7         for(int i=0;i<strs[0].size();i++)
 8         {
 9             char c=strs[0][i];
10             for(int j=1;j<strs.size();j++)
11             {
12                 if(i>=strs[j].size() || strs[j][i]!=c)
13                     return ans;
14             }
15             ans+=c;
16         }
17         return ans;
18     }
19 };
C++

 

字符串的排列

 

给定两个字符串 s1 和 s2，写一个函数来判断 s2 是否包含 s1 的排列。

换句话说，第一个字符串的排列之一是第二个字符串的子串。

示例1:

输入: s1 = "ab" s2 = "eidbaooo"
输出: True
解释: s2 包含 s1 的排列之一 ("ba").

 

示例2:

输入: s1= "ab" s2 = "eidboaoo"
输出: False

 

注意：

  1. 输入的字符串只包含小写字母
  2. 两个字符串的长度都在 [1, 10,000] 之间

 题解：考虑是全排列，那么只要在一段长为s1.length()的区间内s2的每个字符的数量和s1的每个字符的数量相同，那么返回true,否则，没有出现过，返回false;

参考代码：

class Solution {
public:
    bool judge(int a[])
    {
        for(int i=0;i<26;++i)
        {
            if(a[i]!=0) return false;
        }
        return true;
    }
    
    bool checkInclusion(string s1, string s2) 
    {
        if(!s1.length() || !s2.length() || s1.length()>s2.length())
            return false;
        int a[30]={0},flag=0;
        
        for(int i=0;i<s1.length();++i)
            a[s1[i]-'a']--,a[s2[i]-'a']++;
        
        for(int i=s1.length();i<s2.length();++i)
        {
            if(judge(a))
            {
                flag=1;
                break;
            }
            a[s2[i-s1.length()]-'a']--;
            a[s2[i]-'a']++;
        }
        if(judge(a)) flag=1;
        
        if(flag) return true;
        else return false;
    }
};
C++

 

 字符串相乘

 

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

示例 1:

输入: num1 = "2", num2 = "3"
输出: "6"

示例 2:

输入: num1 = "123", num2 = "456"
输出: "56088"

说明：

  1. num1 和 num2 的长度小于110。
  2. num1 和 num2 只包含数字 0-9。
  3. num1 和 num2 均不以零开头，除非是数字 0 本身。
  4. 不能使用任何标准库的大数类型（比如 BigInteger）或直接将输入转换为整数来处理。

 题解：考虑两个数相乘得到的数最后的位数一定 最长是len1+len2长度。

对于s[i]*s[j] 的一定是 ans[i+j+1]的，对于第一个数的每一个i位，我们只要记录一个add就行了

 

参考代码：

class Solution {
public:
    string multiply(string num1, string num2) {
        int l1=num1.size(),l2=num2.size();
        string res(l1+l2,'0');
        if(l1==0||l2==0) return "";
        
        for(int i=l1-1;i>=0;--i)
        {
            int add=0;
            for(int j=l2-1;j>=0;--j)
            {
                int mul=(num1[i]-'0')*(num2[j]-'0');
                int num=res[i+j+1]+add+mul%10-'0';
                res[i+j+1]=num%10+'0';
                add=mul/10+num/10;
            }
            res[i]+=add;
        }
        for(int i=0;i<l1+l2;++i)
            if(res[i]!='0') return res.substr(i);
        return "0";
    }
};
C++

翻转字符串里的单词

 

给定一个字符串，逐个翻转字符串中的每个单词。

 

示例 1：

输入: "the sky is blue"
输出: "blue is sky the"

示例 2：

输入: "  hello world!  "
输出: "world! hello"
解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。

示例 3：

输入: "a good   example"
输出: "example good a"
解释: 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

 

说明：

  • 无空格字符构成一个单词。
  • 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。
  • 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

 

进阶：

请选用 C 语言的用户尝试使用 O(1) 额外空间复杂度的原地解法。

题解：用栈的性质，先存进去（注意把首尾的空格去掉和判断原串是否为空）即可。

 

参考代码：

class Solution {
public:
    string reverseWords(string s) {
        stack<string> str;
        string s0 = "";
        if(s.empty())
        {
            s = "";
            return s;
        }
        for(int i=0;i<s.length();i++)
        {
            if(s[i]!=' ')
            {
                s0+=s[i];
                continue;
            } 
            else if(!s0.empty())
            {
                str.push(s0); 
                s0="";   
            }
        }
        if(!s0.empty())
        {
            str.push(s0);
            s0="";
        }
        while(!str.empty())
        {
            s0+=str.top(); 
            str.pop();
            s0+=" ";
        }
        if(s0.empty())
        {
            s = "";
            return s;
        }
        s0.erase(s0.end()-1);
        s = s0;
        return s;
    }
};
C++

 

简化路径

以 Unix 风格给出一个文件的绝对路径，你需要简化它。或者换句话说，将其转换为规范路径。

在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点 （..） 表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。更多信息请参阅：Linux / Unix中的绝对路径 vs 相对路径

请注意，返回的规范路径必须始终以斜杠 / 开头，并且两个目录名之间必须只有一个斜杠 /。最后一个目录名（如果存在）不能以 / 结尾。此外，规范路径必须是表示绝对路径的最短字符串。

 

示例 1：

输入："/home/"
输出："/home"
解释：注意，最后一个目录名后面没有斜杠。

示例 2：

输入："/../"
输出："/"
解释：从根目录向上一级是不可行的，因为根是你可以到达的最高级。

示例 3：

输入："/home//foo/"
输出："/home/foo"
解释：在规范路径中，多个连续斜杠需要用一个斜杠替换。

示例 4：

输入："/a/./b/../../c/"
输出："/c"

示例 5：

输入："/a/../../b/../c//.//"
输出："/c"

示例 6：

输入："/a//b////c/d//././/.."
输出："/a/b/c"


题解：用vector按照题意模拟即可复原IP地址

参考代码：
class Solution {
public:
    string simplifyPath(string path) 
    {
        vector<string> s;
        int i=0;
        while(i<path.length())
        {
            while(path[i]=='/'&&i<path.length()) ++i;
            if(i==path.length()) break;
            
            int start=i;
            while(path[i]!='/'&&i<path.length()) ++i;
            int end=i;
            
            string cs=path.substr(start,end-start);
            
            if(cs=="..") 
            {
                if(!s.empty())
                    s.pop_back();
            }
            else if(cs!=".") s.push_back(cs);
        }
        if(s.empty()) return "/";
        string ans="";
        for(int j=0;j<s.size();++j)
            ans=ans+'/'+s[j];
        
        return ans;
    }
};
C++

 复原IP地址

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

示例:

输入: "25525511135"
输出: ["255.255.11.135", "255.255.111.35"]

题解：根据Ip地址的性质:4个数字每个数字的范围为0~255，然后暴力枚举每个数字的长度，记录合法的数量即可。

参考代码：
class Solution {
public:
    int getint(string ss)
    {
        if(ss.length()>1 && ss[0]=='0') return 256;
        int num=0;
        for(int i=0;i<ss.length();++i)
            num=num*10+ss[i]-'0';
        return num;
    }
    
    vector<string> restoreIpAddresses(string s) 
    {
        vector<string> v;
        for(int i=1;i<=3;++i)
            for(int j=1;j<=3;++j)
                for(int k=1;k<=3;++k)
                    for(int l=1;l<=3;++l)
                    {
                        if(i+j+k+l==s.length())
                        {
                            int A=getint(s.substr(0,i));
                            int B=getint(s.substr(i,j));
                            int C=getint(s.substr(i+j,k));
                            int D=getint(s.substr(i+j+k,l));
                            if(A<=255 && B<=255 && C<=255 && D<=255)
                            {
                                string res=s.substr(0,i)+"."+s.substr(i,j)+"."+s.substr(i+j,k)+"."+s.substr(i+j+k,l);
                                if(res.length()==s.length()+3) v.push_back(res);
                            }
                        }
                    }
        
        return v;
        
    }
};
View Code

数组与排序

三数之和

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]
题解：我们先对数组sort一下，然后我们知道a+b+c=0;那么这三个数里面的最小的那个数一定是负数,我们枚举最小的那个数的位
注意一定是负数才行，并且和上一个数不同，然后我们定两个指针l=pos+1,r=size()-1;如果a[l]+a[r]>target,r--；如果
a[l]+a[r]<target，则l++,如果等于的话，就记录该情况即可。时间复杂度是O(n^2)

参考代码：
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) 
    {
        vector<vector<int>> ans;
        int len=nums.size();
        sort(nums.begin(),nums.end());
        if (nums.empty() || nums.back() < 0 || nums.front() > 0 || len<3) return {};
        
        for(int k=0;k<nums.size();++k)
        {
            if(nums[k]>0) break;
            if(k>0 && nums[k]==nums[k-1]) continue;
            
            int i=k+1,j=nums.size()-1,target=-nums[k];
            while(i<j)
            {
                if(nums[i]+nums[j]==target) 
                {
                    ans.push_back({nums[k],nums[i],nums[j]});
                    while(i<j && nums[i]==nums[i+1]) ++i;
                    while(i<j && nums[j]==nums[j-1]) --j;
                    ++i;--j;                }
                else if(nums[i]+nums[j]<target) ++i;
                else --j;
                
            }
        }
        return ans;
    }
};
View Code

 

岛屿的最大面积

 

给定一个包含了一些 0 和 1的非空二维数组 grid , 一个 岛屿 是由四个方向 (水平或垂直) 的 1 (代表土地) 构成的组合。你可以假设二维矩阵的四个边缘都被水包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为0。)

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是11，因为岛屿只能包含水平或垂直的四个方向的‘1’。

示例 2:

[[0,0,0,0,0,0,0,0]]

对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

 

题解：典型的DFS题目，我们对每个点打个标记是否被访问过，如果没被访问过并未为‘1’的话，表示找到新的联通快，我们dfs该联通快求得其面积，然后去个最大值即可。

 

参考代码：

class Solution {
public:
    //int vis[52][52];
    int dfs(vector<vector<int>>& grid,int ii,int j)
    {
        //vis[ii][j]=1;
        int n=grid.size();int m=grid[0].size();
        int dx[4]={0,0,1,-1};
        int dy[4]={1,-1,0,0};
        grid[ii][j]=0;
        int sum=1;
        
        for(int i=0;i<4;i++)
        {
            int x=ii+dx[i];
            int y=j+dy[i];
            if(x>=0&&x<n&&y>=0&&y<m&&grid[x][y]==1)
                sum+=dfs(grid,x,y);
        }
        return sum;
    }
    int maxAreaOfIsland(vector<vector<int>>& grid) 
    {
        int n=grid.size();int m=grid[0].size();
        if(n==0)
            return 0;
        int ans=0;
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                //if(vis[i][j]) continue;
                if(grid[i][j]==1)
                {
                    ans=max(dfs(grid,i,j),ans);
                }
            }
        }
        return ans;
    }
};
View Code

搜索旋转排序数组

 

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1
题解：二分。如果右半部分是递增的(a[r]>a[mid]),如果target是介于a[mid]<target<a[r],那么答案在右边。否则答案在左边。
如果左半部分单调，那么如果a[l]<target<a[mid],答案在左边，否则在右边。
 
参考代码：
class Solution {
public:
    int search(vector<int>& nums, int target) 
    {
        int ans=-1;
        int l=0,r=nums.size()-1;
        while(l<=r)
        {
            int mid=l+r>>1;
            if(nums[mid]==target) 
            {
                ans=mid;
                break;
            }
            if(nums[mid]<nums[r])
            {
                if(nums[mid]<target&&target<=nums[r]) l=mid+1;
                else r=mid-1;
            }
            else
            {
                if(nums[l]<=target&&target<nums[mid]) r=mid-1;
                else l=mid+1;
            }
        }
        return ans;
    }
};
View Code

 

最长连续递增序列

 

给定一个未经排序的整数数组，找到最长且连续的的递增序列。

示例 1:

输入: [1,3,5,4,7]
输出: 3
解释: 最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为5和7在原数组里被4隔开。

示例 2:

输入: [2,2,2,2,2]
输出: 1
解释: 最长连续递增序列是 [2], 长度为1。

注意：数组长度不会超过10000。

题解：直接记录就行了O(N)。

 

参考代码：

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) 
    {
        if(nums.size()==0) return 0; 
        int ans=1,tmp=nums[0],res=1;
        
        for(int i=1;i<nums.size();++i)
        {
            if(nums[i]>tmp)
            {
                ++res;
                tmp=nums[i];
            }
            else
            {
                ans=max(ans,res);
                res=1;tmp=nums[i];
            }
        }
        return max(ans,res);
    }
};
View Code

数组中的第K个最大元素

 

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

 题解：类似快排思想。我们每次取a[l],然后从l+1~r,将比a[l]小的数放到a[l]左边，比a[l]大的数放到a[l]右边。最后返回a[l]的位置pos和n-k比较，如果pos==n-k,那么pos就是答案，如果pos<n-k,l=pos+1.如果pos>n-k，那么r=pos-1.

期望时间复杂度O(N)。

参考代码：

class Solution {
public:
    
    int patition(vector<int>&nums,int L,int R)
    {
        int tmp=nums[L];
        int l=L+1,r=R;
        while(l<=r)
        {
            while(l<=r && nums[r]>=tmp) --r;
            while(l<=r && nums[l]<=tmp) ++l;
            if(l>r) break;
            swap(nums[l],nums[r]);
            l++,r--;
        }
        swap(nums[L],nums[r]);
        return r;
    }
        
    
    int findKthLargest(vector<int>& nums, int k) 
    {
        int l=0,r=nums.size()-1;
        int n=r+1;
        if(n==1) return nums[0];
        
        while(true)
        {
            int pos=patition(nums,l,r);
            if(pos==n-k) return nums[pos];
            if(pos>n-k) r=pos-1;
            else l=pos+1;
        }
    }
};
View Code

 

最长连续序列

 

给定一个未排序的整数数组，找出最长连续序列的长度。

要求算法的时间复杂度为 O(n)。

示例:

输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。

题解：由于时间复杂度是O(N),所以我们可以想到unordered_set<int>,可以再O(N)时间内保证里面的元素有序。
然后对于一个数nums[pos]，我们判断是否为开始就行了，如果是，依次判断后面的数是否都有即可。

参考代码：
class Solution {
public:
    int longestConsecutive(vector<int>& nums) 
    {
        int res=0;
        unordered_set<int> st(nums.begin(),nums.end());
        for(auto num:nums)
        {
            if(st.count(num-1)==0)
            {
                int x=num+1;
                while(st.count(x)) ++x;
                res = max(res, x-num);
            }
        }
        return res;
    }
};
View Code

第k个排列

 

给出集合 [1,2,3,…,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

  1. "123"
  2. "132"
  3. "213"
  4. "231"
  5. "312"
  6. "321"

给定 n 和 k，返回第 k 个排列。

说明：

  • 给定 n 的范围是 [1, 9]。
  • 给定 k 的范围是[1,  n!]。

示例 1:

输入: n = 3, k = 3
输出: "213"

示例 2:

输入: n = 4, k = 9
输出: "2314"

题解：对有个位置pos，如果pos对应的书生一位，那么对用增加其后面所有数的全排列。

 

参考代码：

class Solution {
public:
    string getPermutation(int n, int k) 
    {
        string s="123456789",ans="";
        vector<int> f(n,1);
        for(int i=1;i<n;++i)
            f[i]=f[i-1]*i;
        --k;
        for(int i=n-1;i>=0;--i)
        {
            int j=k/f[i];
            k%=f[i];
            ans=ans+s[j];
            s.erase(j,1);
        }
        return ans;
    }
};
View Code

 

朋友圈

 

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

示例 1:

输入: 
[[1,1,0],
 [1,1,0],
 [0,0,1]]
输出: 2 
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。

示例 2:

输入: 
[[1,1,0],
 [1,1,1],
 [0,1,1]]
输出: 1
说明：已知学生0和学生1互为朋友，学生1和学生2互为朋友，所以学生0和学生2也是朋友，所以他们三个在一个朋友圈，返回1。

注意：

  1. N 在[1,200]的范围内。
  2. 对于所有学生，有M[i][i] = 1。
  3. 如果有M[i][j] = 1，则有M[j][i] = 1。

题解：并查集即可。

 

参考代码：

class Solution {
public:
    int fa[210],vis[210];
    int Find(int x){return x==fa[x]? x:fa[x]=Find(fa[x]);}
    void Union(int x,int y)
    {
        int fx=Find(x),fy=Find(y);
        fa[fx]=fy;
    }
    int findCircleNum(vector<vector<int>>& M) 
    {
        int N=M.size(),ans=0;
        for(int i=1;i<=N;++i) fa[i]=i;
        for(int i=0;i<N;++i)
        {
            for(int j=0;j<N;++j)
            {
                if(M[i][j]==1) 
                    Union(i+1,j+1);
            }
        }
        for(int i=1;i<=N;++i)
            vis[Find(i)]=1;
        for(int i=1;i<=N;++i) if(vis[i]==1) ans++;
        return ans;
    }
};
View Code

 

合并区间

 

给出一个区间的集合，请合并所有重叠的区间。

示例 1:

输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2:

输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

题解：按照左边界为第一关键字，由边界为第二关键字，排下序。然后合并区间就行了。

 

参考代码：

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& v) 
    {
        vector<vector<int>> ans;
        int len=v.size();
        if(len==0) return {};
        
        pair<int,int> p[len];
        for(int i=0;i<len;++i)
        {
            p[i].first=v[i][0];
            p[i].second=v[i][1];
        }
        sort(p,p+len);
        pair<int,int> pi;
        pi.first=p[0].first;pi.second=p[0].second;
        
        for(int i=1;i<len;++i)
        {
            if(p[i].first<=pi.second)
                pi.second=max(pi.second,p[i].second);
            else
            {
                ans.push_back({pi.first,pi.second});
                pi.first=p[i].first;pi.second=p[i].second;
            }
        }
        ans.push_back({pi.first,pi.second});
        
        return ans;
    }
};
View Code

  接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

题解：先找到最高位置pos,然后从最左边和最右边往中间靠。记录另一个边界的最大值。根据情况判断加或不加。

 

参考代码：

class Solution {
public:
    int trap(vector<int>& height) {
        int n=height.size();
        if(n<=2)
            return 0;
        int maxx=-1;int id;
        for(int i=0;i<n;i++)
        {
            if(height[i]>maxx)
            {
                maxx=height[i];
                id=i;
            }
        }
        int ans=0;int t=height[0];
        for(int i=0;i<id;i++)
        {
            if(t<height[i])
                t=height[i];
            else
                ans+=(t-height[i]);
        }
        t=height[n-1];
        for(int i=n-1;i>id;i--)
        {
            if(t<height[i])
                t=height[i];
            else
                ans+=(t-height[i]);
        }
        return ans;
    }
};
View Code 

链表和树

合并两个有序链表

 

将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 

示例：

输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

题解：创建新的头指针，然后当l1和l2都不是空的时候，判断哪一个小，让新的头指向该节点，并将小的链表向后移动一位。然后l1和l2至少有一个为空，这时候，我们找到不空的，把它接到l3后面即可，最后返回l3的头指针。

 

参考代码：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) 
    {
        ListNode l3=new ListNode(0);
        ListNode l4=l3;
        while(l1!=null && l2!=null)
        {
            if(l1.val<=l2.val) 
            {
                l3.next=l1;
                l1=l1.next;
            }
            else 
            {
                l3.next=l2;
                l2=l2.next;
            }
            l3=l3.next;
        }
        if(l1!=null) l3.next=l1;
        else if(l2!=null) l3.next=l2;
        return l4.next;
    }
}
Java

 

 反转链表

 

反转一个单链表。

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

进阶:
你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

 题解：记录三个指针即可。

 

参考代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode *ans=NULL;
        ListNode *pre=NULL;
        ListNode *temp=head;
        while(temp!=NULL)
        {
            ListNode *nextt=temp->next;
            if(nextt==NULL)
                ans=temp;
            temp->next=pre;
            pre=temp;
            temp=nextt;
        }
        return ans;
    }
};
C++
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) 
    {
        if(head.next==null) return head;
        if((head.next).next==null)
        {
            (head.next).next=head;
            head.next=null;
            return head.next;
        }
        ListNode pre=new ListNode(0),now=new ListNode(0),nxt=new ListNode(0);
        while(head!=null)
        {
            now=head;
            nxt=head.next;
            
            now.next=pre;
            pre=nxt.next;
            nxt.next=now;
            now.next=pre;
            pre=now;now=nxt;
            
            head=head.next;
        }
        return pre;
    }
}
Java

 

两数相加

 

给出两个 非空 的链表用来表示两个非负的整数。其中，它们各自的位数是按照 逆序 的方式存储的，并且它们的每个节点只能存储 一位 数字。

如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。

您可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例：

输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 0 -> 8
原因：342 + 465 = 807

题解：

 

参考代码：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode l3 = new ListNode(0);
        ListNode res = l3;
        int value = 0;
        int flag = 0;
        while (l1 != null || l2 != null || flag == 1) {
            int sum = flag;
            sum += (l1 != null ? l1.val : 0) + (l2 != null ? l2.val : 0);
            l1 = (l1 != null ? l1.next : null);
            l2 = (l2 != null ? l2.next : null);
            l3.next = new ListNode(sum % 10);
            flag = sum / 10;
            l3 = l3.next;
        }
        return res.next;
    }
}
Java

 

排序链表

 

在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。

示例 1:

输入: 4->2->1->3
输出: 1->2->3->4

示例 2:

输入: -1->5->3->4->0
输出: -1->0->3->4->5

题解：

吧链表中的数存到vector中，然后sort一下，重新插入到链表中去。

参考代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        vector<int> v;
        ListNode *p=head;
        while(p!=NULL)
        {
            v.push_back((p->val));
            p=p->next;
        }
        sort(v.begin(),v.end());
        p=head;
        int i=0;
        while(p!=NULL)
        {
            p->val=v[i++];
            
            p=p->next;
        }
        return head;
    }
};
C++
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode sortList(ListNode head) 
    {
        Vector<int> v=new Vector<int>();
        ListNode p=head;
        while(p!=null)
        {
            v.push_back(p.val);
            p=p.next;
        }
        sort(v.begin(),v.end());
        p=head;
        while(p!=null)
        {
            p.val=v[0];
            v.pop_back();
        }
        return head;
    }
}
Java

环形链表 II

 

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

 

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：no cycle
解释：链表中没有环。

 

进阶：
你是否可以不用额外空间解决此题？

题解：

　　快慢指针法。f(快指针)，l(慢指针).每次快指针移动两步，慢指针移动一步。如果有一个指针为null,那么不存在环，当快指针追上慢指针的时候，此时快指针比慢指针多走了一个环的距离，而慢指针则走了一个环的长度，。然后我们让快指针指向链表头，然后再次移动，此时快慢指针每次都移动一步，当再次碰面的时候，快指针指向的节点就是环的入口，返回即可。

参考代码：

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {//快慢指针法
    public ListNode detectCycle(ListNode head) 
    {
        ListNode f=head,l=head;
        while(true)
        {
            if(f==null || f.next==null) return null;
            f=f.next.next;
            l=l.next;
            if(f==l) break;
        }
        f=head;
        while(f!=l)
        {
            f=f.next;
            l=l.next;
        }
        return f;
    }
}
Java

相交链表

 

编写一个程序，找到两个单链表相交的起始节点。

如下面的两个链表：

在节点 c1 开始相交。

 

示例 1：

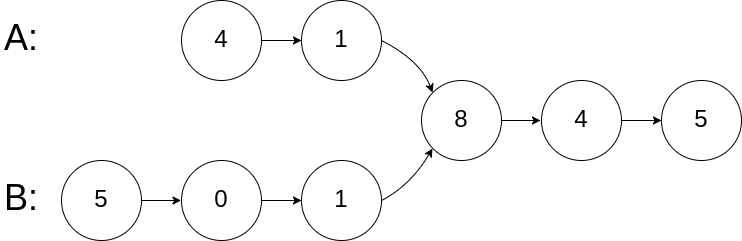
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Reference of the node with value = 8
输入解释：相交节点的值为 8 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

 

示例 2：

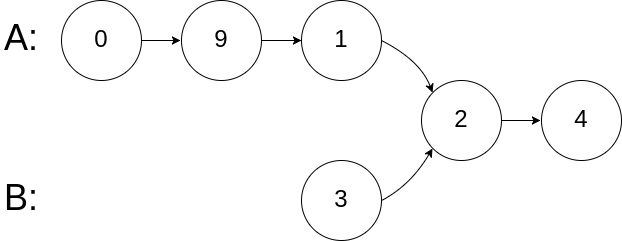
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Reference of the node with value = 2
输入解释：相交节点的值为 2 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

 

示例 3：

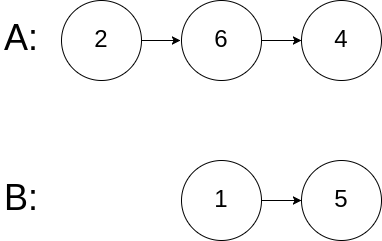
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
输入解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
解释：这两个链表不相交，因此返回 null。

 

注意：

  • 如果两个链表没有交点，返回 null.
  • 在返回结果后，两个链表仍须保持原有的结构。
  • 可假定整个链表结构中没有循环。
  • 程序尽量满足 O(n) 时间复杂度，且仅用 O(1) 内存。

题解：分别使用两个指针l1,l2指向两个链表，然后假设(l1>l2,长度)，当l2走到尽头的时候，令l2指向第一个链表的头，继续走。当l1为null的时候，令l1指向第一个链表的头，此时，l1和l2距离末尾的长度都是l2的长度，然后，两个指针同时移动，当l1==l2时，该节点就是相交的第一个节点，返回即可。

参考代码：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) 
    {
        if(headA==null || headB==null) return null;
        ListNode la=headA,lb=headB;
        while(la!=lb)
        {
            if(la==null) la=headB;else la=la.next;
            if(lb==null) lb=headA;else lb=lb.next;
        }
        return la;
    }
}
Java

 

 合并K个排序链表

 

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

输入:
[
  1->4->5,
  1->3->4,
  2->6
]
输出: 1->1->2->3->4->4->5->6

题解：

暴力找最小的，然后把对应的节点往后移动一位即可。

参考代码：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) 
    {
        ListNode ans=new ListNode(0);
        ListNode res=ans;
        while(true)
        {
            int min_val=Integer.MAX_VALUE;
            int pos=-1;
            for(int i=0;i<lists.length;++i)
            {
                if(lists[i]!=null)
                {
                    if(lists[i].val<min_val)
                    {
                        min_val=lists[i].val;
                        pos=i;
                    }
                }
            }
            if(min_val==Integer.MAX_VALUE)
                break;
            ListNode node=new ListNode(min_val);
            ans.next=node; ans=ans.next;
            
            lists[pos]=lists[pos].next;
        }
        return res.next;
    }
}
Java

 

 二叉树的最近公共祖先

 

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树:  root = [3,5,1,6,2,0,8,null,null,7,4]

 

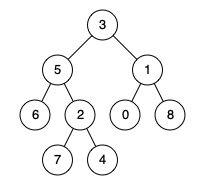
示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

 

说明:

  • 所有节点的值都是唯一的。
  • p、q 为不同节点且均存在于给定的二叉树中。

题解：递归。

　　两个节点要么是父子关系，要么在一个root下，我们们判断root是否为p或q,是的话，就返回root.

然后递归左右子树，如果left!=null&&right!=null则返回root.

如果left==null,则返回右子树的递归结果，否则返回左子树的递归结果。

 

参考代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) 
    {
        if(root==null) return root;
        if(root==p||root==q) return root;
        TreeNode left=lowestCommonAncestor(root.left,p,q);
        TreeNode right=lowestCommonAncestor(root.right,p,q);
        
        if(left!=null && right!=null) return root;
        if(left==null) return right;
        else return left;
    }
}
Java

 

二叉树的锯齿形层次遍历

 

给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如：
给定二叉树 [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回锯齿形层次遍历如下：

[
  [3],
  [20,9],
  [15,7]
]

题解：类似BFS.我们用队列存储每一层的节点，并记录深度，然后一层一层往下扩展，如果深度为偶数，则反转list即可。

参考代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public List<List<Integer>> data = new ArrayList<List<Integer>>();

    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        if(root == null){
            return data;
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        int level = 1;
        while(!queue.isEmpty()){
            int size = queue.size();
            List<Integer> list = new ArrayList<Integer>();
            for(int  i = 0; i < size; i++){
                TreeNode node = queue.poll();
                list.add(node.val);
                if(node.left != null){
                    queue.offer(node.left);
                }
                if(node.right != null){
                    queue.offer(node.right);
                }
            }
            if(level % 2 != 0){
                data.add(list);
            }else{
                Collections.reverse(list);
                data.add(list);
            }
            level++;
        }
        return data;
    }
}
Java

 

动态或贪心

 

买卖股票的最佳时机

 

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

题解：

记录前缀最小值即可。

参考代码：

class Solution {
public:
    int maxProfit(vector<int>& p) 
    {
        if(p.size()==0) return 0;
        int min_val=p[0],ans=0;
        for(int i=1,len=p.size();i<len;++i)
        {
            ans=max(ans,p[i]-min_val);
            min_val=min(min_val,p[i]);
        }
        return ans;
    }
};
C++

买卖股票的最佳时机 II

 

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

题解：如果递减就一直更新找到最小值，然后如果一直增加就先不买，当下一天降的时候，就买了，然后继续前面的操作，记录和即可。

 

参考代码：

class Solution {
public:
    int maxProfit(vector<int>& p) 
    {
        if(p.size()==0) return 0;
        int ans=0,min_val=p[0],max_val=p[0];
        int len=p.size(),pos=1;
        
        while(pos<len)
        {
            while(min_val>=p[pos]) 
            {
                min_val=p[pos];
                pos++;
                if(pos>=len) break;
            }
            if(pos>=len) break;
            max_val=min_val;
            int res=0;
            while(max_val<=p[pos])
            {
                max_val=p[pos];
                res=max_val-min_val;
                pos++;
                if(pos>=len) break;
            }
            min_val=p[pos];
            ans+=res;
        }
         return ans;
    }
   
};
C++

 

最大正方形

 

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

示例:

输入: 

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

输出: 4

题解：DP。

　　对于一全1的边长你为n正方形的右下角那个1，则其左边，上边和左上边，一定全部是边长为n-1的正方形。如果不是，则取这三个正方形边长的最小值即可。

　　转移方程：dp[i][j]=min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1]))+1;

 

参考代码：

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) 
    {
        if(matrix.size()==0) return 0;
        if(matrix[0].size()==0) return 0;
        int n=matrix.size(),m=matrix[0].size();
        
        int dp[n][m],ans=0;
        memset(dp,0,sizeof dp);
        for(int i=0;i<n;++i)
        {
            if(matrix[i][0]=='1')
                dp[i][0]=1,ans=1;
        }
        for(int i=0;i<m;++i)
        {
            if(matrix[0][i]=='1')
                dp[0][i]=1,ans=1;
        }
        
        for(int i=1;i<n;++i)
        {
            for(int j=1;j<m;++j)
            {
                if(matrix[i][j]=='1')
                {
                    dp[i][j]=min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1]))+1;
                    ans=max(ans,dp[i][j]);
                }
            }
        }
        return (ans*ans);
    }
};
C++

 

 

最大子序和

 

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

进阶:

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

 题解：

记录最小前缀和，和前缀和。

参考代码：

普通：

class Solution {
public:
    int maxSubArray(vector<int>& nums) 
    {
        if(nums.size()==0) return 0;
        int ans=nums[0],min_val=nums[0],now=nums[0];
        
        for(int i=1;i<nums.size();++i)
        {
            now+=nums[i];
            ans=max(ans,max(now,now-min_val));
            min_val=min(min_val,now);
        }
        return ans;
    }
};
C++

进阶：

class Solution {
public:
    int work(int l,int r,vector<int>&v)
    {
        if(l==r) return v[l];
        int mid=l+r>>1;
        int ans=max(work(l,mid,v),work(mid+1,r,v));
        int numl=v[mid],numr=v[mid+1],res=v[mid];
        for(int i=mid-1;i>=l;--i)
        {
            res+=v[i];
            numl=max(numl,res);
        }
        res=v[mid+1];
        for(int i=mid+2;i<=r;++i)
        {
            res+=v[i];
            numr=max(numr,res);
        }
        return max(ans,numl+numr);
    }
    
    
    int maxSubArray(vector<int>& nums) 
    {
        if(nums.size()==0)
            return 0;
        return work(0,nums.size()-1,nums);
    }
};
C++

 

 三角形最小路径和

 

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：

如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

 

题解：DP;

dp[i][j]:表示第i行第j个位置时的最小路径和。这里我们可以优化一维空间，dp[i]和p[j]两个数组分别表示当前行和上一行的路径和即可。

时间复杂度O(N^2); 空间复杂度O(N);

 

参考代码：

class Solution {
public:
    int minimumTotal(vector<vector<int>>& t) 
    {
        if(t.size()==0) return 0;
        int n=t.size(),m=t.size();
        int dp[m]={0},d[m]={0};
        
        for(int i=0;i<m;++i)
            d[i]=t[n-1][i];
        
        for(int i=n-2;i>=0;--i)
        {
            for(int j=0;j<t[i].size();++j)
            {
                dp[j]=min(d[j],d[j+1])+t[i][j];
                d[j]=dp[j];
            }
        }
        return d[0];
    }
};
C++

 

俄罗斯套娃信封问题

 

给定一些标记了宽度和高度的信封，宽度和高度以整数对形式 (w, h) 出现。当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。

请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。

说明:
不允许旋转信封。

示例:

输入: envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出: 3 
解释: 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。

题解：DP。

dp[i]:表示前i个信封所能得到的最大值。先按信封的w,h为第一，第二关键字排下序。

转移方程：dp[i]=max(dp[i],dp[j]+1);

参考代码：

class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& e) 
    {
        if(e.size()==0) return 0;
        int n=e.size();
        pair<int,int> p[n];
        for(int i=0;i<e.size();++i)
        {
            p[i].first=e[i][0];
            p[i].second=e[i][1];
        }
        sort(p,p+n);
        
        int dp[n],ans=1;
        for(int i=0;i<n;++i) dp[i]=1;
        
        for(int i=0;i<n;++i)
        {
            for(int j=0;j<i;++j)
            {
                if(p[j].first<p[i].first&&p[j].second<p[i].second)
                    dp[i]=max(dp[i],dp[j]+1);
            }
            ans=max(ans,dp[i]);
        }
        return ans;
    }
};
C++

 

数据结构

最小栈

 

设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。

  • push(x) -- 将元素 x 推入栈中。
  • pop() -- 删除栈顶的元素。
  • top() -- 获取栈顶元素。
  • getMin() -- 检索栈中的最小元素。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

题解：

用两个栈模拟即可。一个普通栈，一个单调栈。

参考代码：

class MinStack {
public:
    /** initialize your data structure here. */
    MinStack() {}
    
    void push(int x) {
        s1.push(x);
        if (s2.empty() || x <= s2.top()) s2.push(x);
    }
    
    void pop() {
        if (s1.top() == s2.top()) s2.pop();
        s1.pop();
    }
    
    int top() {
        return s1.top();
    }
    
    int getMin() {
        return s2.top();
    }
    
private:
    stack<int> s1, s2;
};
C++

 

LRU缓存机制

 

运用你所掌握的数据结构，设计和实现一个  LRU (最近最少使用) 缓存机制。它应该支持以下操作： 获取数据 get 和 写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

进阶:

你是否可以在 O(1) 时间复杂度内完成这两种操作？

示例:

LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // 返回  1
cache.put(3, 3);    // 该操作会使得密钥 2 作废
cache.get(2);       // 返回 -1 (未找到)
cache.put(4, 4);    // 该操作会使得密钥 1 作废
cache.get(1);       // 返回 -1 (未找到)
cache.get(3);       // 返回  3
cache.get(4);       // 返回  4

题解：

按题意的来嘛，用Map加Stack就可以解决了。

参考代码：

class LRUCache {
 
    Map<Integer,Integer> map ;
    Stack<Integer> stack;
    int size;
    
    public LRUCache(int capacity) {
        stack = new Stack<>();
        map = new HashMap<>(capacity);
        size = capacity;
    }
    
    public int get(int key) {
        if(!stack.contains(key)){
            return -1;
        }
        boolean flag = stack.remove(Integer.valueOf(key));
        stack.push(key);
        return map.get(key);
    }
    
    public void put(int key, int value) {
        if(stack.contains(key)){
            stack.remove(Integer.valueOf(key));
        }else{
            if(stack.size() == size){
                int count = stack.remove(0);
                map.remove(count);
            }
        }
        stack.push(key);
        map.put(key,value);
    }
}
C++
posted @ 2019-11-28 20:56  StarHai  阅读(3753)  评论(0)  编辑  收藏  举报