洛谷P2569 (BZOJ1855)[SCOI2010]股票交易 【单调队列优化DP】
Description
最近lxhgww又迷上了投资股票,通过一段时间的观察和学习,他总结出了股票行情的一些规律。 通过一段时间的观察,lxhgww预测到了未来T天内某只股票的走势,第i天的股票买入价为每股APi,第i天的股票卖出价为每股BPi(数据保证对于每个i,都有APi>=BPi),但是每天不能无限制地交易,于是股票交易所规定第i天的一次买入至多只能购买ASi股,一次卖出至多只能卖出BSi股。 另外,股票交易所还制定了两个规定。为了避免大家疯狂交易,股票交易所规定在两次交易(某一天的买入或者卖出均算是一次交易)之间,至少要间隔W天,也就是说如果在第i天发生了交易,那么从第i+1天到第i+W天,均不能发生交易。同时,为了避免垄断,股票交易所还规定在任何时间,一个人的手里的股票数不能超过MaxP。 在第1天之前,lxhgww手里有一大笔钱(可以认为钱的数目无限),但是没有任何股票,当然,T天以后,lxhgww想要赚到最多的钱,聪明的程序员们,你们能帮助他吗?
Input
输入数据第一行包括3个整数,分别是T,MaxP,W。 接下来T行,第i行代表第i-1天的股票走势,每行4个整数,分别表示APi,BPi,ASi,BSi。
Output
输出数据为一行,包括1个数字,表示lxhgww能赚到的最多的钱数。
Sample Input
5 2 0
2 1 1 1
2 1 1 1
3 2 1 1
4 3 1 1
5 4 1 1
2 1 1 1
2 1 1 1
3 2 1 1
4 3 1 1
5 4 1 1
Sample Output
3
HINT
对于30%的数据,0 < =W 对于50%的数据,0 < =W 对于100%的数据,0 < =W
对于所有的数据,1 < =BPi < =APi < =1000,1 < =ASi,BSi < =MaxP
题解:设f[i][j]表示第i天持有j股股票能获得的做大利润

对于买入,我们可以变形:
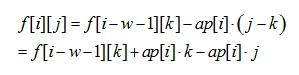
那么可以用单调队列维护f[i-w-1][k]+ap[i]*k(因为对于固定的i,ap[i]是固定的),这样f[i][j]就能做到O(1)计算,而不必枚举k。卖出也一样。
参考代码:

#include<bits/stdc++.h> using namespace std; typedef long long ll; #define pii pair<int,int> #define pil pair<int,ll> #define mkp make_pair #define fi first #define se second const int INF=0x3f3f3f3f; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} return x*f; } const int maxn=2019; int n,m,w; int dp[maxn][maxn],q[maxn]; int main() { n=read();m=read();w=read(); int ap,bp,as,bs,ans=0; memset(dp,128,sizeof(dp)); for(int i=1;i<=n;++i) { ap=read();bp=read();as=read();bs=read(); for(int j=0;j<=as;++j) dp[i][j]=-j*ap;//直接购买股票 for(int j=0;j<=m;++j) dp[i][j]=max(dp[i][j],dp[i-1][j]);//未到第w+1天不能出售 if(i<=w) continue; int l=0,r=0; for(int j=0;j<=m;++j)//在之前的基础上买股票 { while(l<r && q[l]<j-as) ++l;//把超出范围的去掉 while(l<r&&dp[i-w-1][q[r-1]]+q[r-1]*ap<=dp[i-w-1][j]+j*ap) --r; q[r++]=j; if(l<r) dp[i][j]=max(dp[i][j],dp[i-w-1][q[l]]+q[l]*ap-j*ap); } l=0,r=0; for(int j=m;j>=0;--j)//在之前的基础上卖股票 { while(l<r && q[l]>j+bs) ++l; while(l<r&&dp[i-w-1][q[r-1]]+q[r-1]*bp<=dp[i-w-1][j]+j*bp) --r; q[r++]=j; if(l<r) dp[i][j]=max(dp[i][j],dp[i-w-1][q[l]]+q[l]*bp-j*bp); } } for(int i=0;i<=m;++i) ans=max(ans,dp[n][i]); printf("%d\n",ans); return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号