基础
信息在计算机中都是以0、1来表示的,这一点不用赘述。
bit:每一个表示0、1的内存位,叫做bit(位)。
byte:现代计算机大多用8位的内存块作为最小可寻址内存单位,叫做byte(字节)
十六进制表示法:
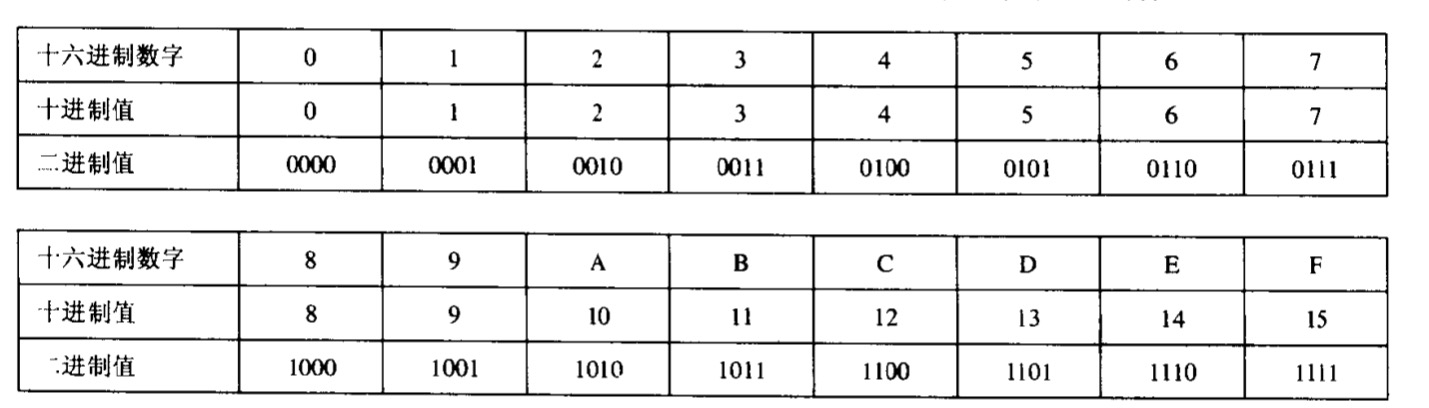
一般认为,以0X开头的数字常量是十六进制的值。进制对应关系如下:
数据寻址/字节顺序
虚拟内存:计算机程序会将内存视为一个非常大的连续的byte数组,这个byte数组就是虚拟内存。
数组里每一个byte都有一个唯一数字来标识,这个数字就是内存地址。
现实中,很多信息、变量都是大于一个byte的,无法用一个单纯的内存地址来表示。
因此,首先需要一个内存地址,在加上对应数据类型的偏移量,这样就可以明确这个信息对应的内存区域了。
然后还需要一个规定的存储顺序。最高有效位 -> 最低有效位 这种称为大端法,最低有效位 -> 最高有效位这种称为小端法。
举例:
十进制:2190,二进制:00001000 10001110,16进制:0x088e
这个如果用大端法表示,那就是 00001000 10001110;
如果用小端法表示,那就是 10001110 00001000。
目前大多数操作系统都是用小端法表示的(Windows、Android、IOS)
提问:大端法、小端法有什么优缺?为什么会出现两种方式?为什么大多数计算机都采用了小端法?
位运算
布尔运算
假设有两个bit,值分别是p和q;
~:
非,NOT。
1010~ = 0101
&:
与,AND,p=1且q=1是才为1。
1010 & 1100 = 1000
|:
或,OR,p=1或q=1时为真。
1010 | 1100 = 1110
^:
异或,(p=1或q=1) 且 p!=q时为真。
1010 ^ 1100 = 0110;1100 ^ 1100 = 0000;
习题
1、判断数字奇偶性
2、一个集合里,有一个数字出现了一次,其他所有数字都出现了两次,求这个出现了一次的数字。
移位运算
位移描述的实际上是数学上的高位/低位的移位运动,不是指实际的内存移动。
例如,左移就是低位往高位移动。大端法是向左移动,小端法是向右移动。
右移反之。
左移:<<,移动后右侧补零;
算数右移:>>,移动后补最高有效位的值;
逻辑右移 >>>,移动后左侧补0:
|
|
数1 |
数2 |
|
原始值 |
0110 0011 |
1001 0101 |
|
x << 4 |
0011 0000 |
0101 0000 |
|
x >>> 4(逻辑右移) |
0000 0110 |
0000 1001 |
|
x >> 4 (算术右移) |
0000 0110 |
1111 1001 |
左移 等于 乘以2;
右移等于 除以2;
为什么会有算术右移和逻辑右移?
整形表示
无符号(原码)
假设有一个整数数据类型有w位,我们可以将位向量写成,表示整个向量。
表示向量中的每一位。在这个编码中,每一位都取0或者1。
用一个公式(binary to unsigned,二进制转无符号数,长度为w)来表示:
这个公式就是二进制向无符号整形的转换计算过程。
下面说人话:
0000 1000 转化为无符号整形的过程:
意思就是 0000 1000 这个二进制byte在无符号整形表示法下,实际的值是 8 。
提问:如何表示负数?
有符号(补码)
顶一个一个函数:
对于向量:
说人话:
0000 1000:
1110 1000:
1111 1111 = -1;
1000 0000 = -128
除了负整数除以2等于其右移1位加1外,所有的整数除以2与右移1位等价。
浮点数
二进制小数
学习浮点数表示有一个前提,就是要明白二进制小数的含义。
一个形如:
的表示法,每一位的取值范围是0和1,这种表示法表示的数字b的定义如下:
说人话:
1001.0011 = =
也就是9.1875。
小数点左移一位:100.10011 = 4.59375
小数点右移一位:10010.001 = 18.375
提问:小数点左移右移有什么含义?
IEEE浮点数
这个就不详细描述定义了,太复杂了。直接说人话。
大体就是把一个浮点数表示为尾数乘以2的指数次方再添上符号。float和double的规格如下:
符号位 阶码 尾数 长度
float 1 8 23 32
double 1 11 52 64
先解释一下这几个部分:
符号位s表示正负,0是正1是负;
尾数M表示的含义是一个形如 1.00110.....的二进制小数,整数位都是有且仅有1。因为每个尾数都是整数部分只有1,所以保存时去掉整数位的1,只保留小数点后面的部分。
阶码E表示的是,尾数M 需要乘以 2的E次幂,才能得到实际表示的值。E也不是直接存储的字面值,而是有一些隐含逻辑。
实例讲解:
1、求38414.4D的IEEE二进制表示法
此数是Double,64位,阶码11位,尾数有52位。
符号位s:正数,为0;
尾数M:38414.4,用二进制表示是:0.4=0.5*0+0.25*1+0.125*1+0.0625*0+……
这个永远也写不完,这时候就只取53位(尾数可以放52位,最前面一位可以省略)
38414.4(10)=1001011000001110.0110011001100110011001100110011001100(2)
=1.001011000001110 0110011001100110011001100110011001100(2) *
标红部分S就是存到尾数M里的数据;
这时候来算阶码E:
在算尾数时,后面的2^15就是算阶码的关键。阶码的作用就是把尾数还原成二进制小数。如果想把S转换成实际的二进制小数,则需要1.S * 2^15次方,而E存储的就是这个15次幂这个信息。
Double的阶码有11位,可以保存-1024 ~ 1023这个范围的指数。因为指数是可以为负的,为了方便保存、计算,这里并没有采用补码来保存阶码,而是用移码,也就是实际指数 + 1023。这样做的好处是可以方便的比较浮点数大小,提升效率。11位无符号可以表示0-2047范围的数字。
那么15对应的阶码E就是15+1023 = 1038,二进制:100 00001110;
那么38414.4D在内存中的存储就是:
0 10000001110 0010 11000001 110 01100 11001100 11001100 11001100 11001100
问题1:如果表示0?如何表示无穷大?
问题2:阶码移码的表示范围?
用阶码全0 尾数全0表示0,用阶码全1尾数为0表示无穷大;
11为阶码能表述的无符号数范围就只剩下1-2046这个范围了,减去1023,则就对应的实际指数表示范围就是-1022~1023这个范围。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号