10-K最近邻算法

本章内容：

• 学习使用K最近邻算法创建分类系统
• 学习特征抽取
• 学习回归，即预测数值，如明天的股价或用户对某部电影对喜欢程度
• 学习K最近邻算法的应用案例和局限性

1.橙子还是柚子

猜这个水果是柚子，还是橙子？
如果又红又大，很可能是柚子；反之可能是橙子。
如何判断这个水果是橙子，还是柚子？
一种办法是看它的邻居。
在这三个邻居中，橙子比柚子多，因此这个水果很可能是橙子。这就是K最近邻算法。

2.创建推荐系统

假设要为用户创建一个电影推荐系统。从本质上说，这类似于水果问题。
将所有的用户都放入一个图表中。这些用户在图表中的位置取决于其喜好，因此喜好相似的用户距离较近。假设你要向张翠山推荐电影，可以找出6位与他最接近的用户。

假设在电影的喜好方面，宋远桥、俞莲舟、俞岱岩、张松溪、殷梨亭、莫声谷都与张翠山差不多，因此它们喜欢的电影很可能张翠山也喜欢。
有了这样的图表，创建推荐系统就将易如反掌：只要宋远桥喜欢的电影，就将其推荐给张翠山。
问题：如何确定两位用户的相似度呢？

2.1特征抽取

在前面的水果示例中，你根据个头和颜色来比较水果，即比较的特征是个头和颜色。现在假设有三个水果，你可抽取它们的特征。
再根据这些特征绘图。

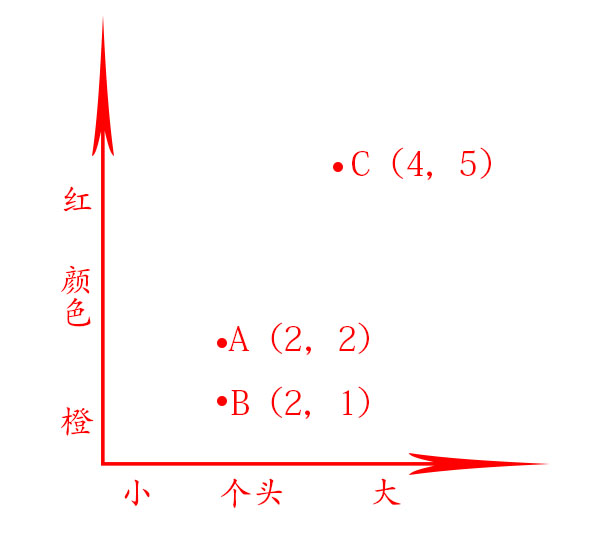
从上图可知，水果A和B比较像。下面来度量它们有多像。要计算两点的距离，可使用毕达哥拉斯公式\(\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2})}\).
例如A和B的距离如下：\(\sqrt{(2-2)^{2}+(2-1)^{2})}\) = \(\sqrt{0+1}\) = \(\sqrt{1}\) = 1
A和C的距离如下：\(\sqrt{(4-2)^{2}+(5-1)^{2})}\) = \(\sqrt{4+16}\) = \(\sqrt{20}\) = 4.47

在电影推荐系统中，需要将每位用户都转换为一组坐标，就像前面对水果所做的那样。在能够将用户放入图表后，就可以计算他们之间的距离了。
用户注册时，要求它们指出对各种电影的喜欢程度。这样每位用户都将获得一组数字。如

	张翠山	宋远桥	张松溪
喜剧片	3	4	2
动作片	4	3	5
生活片	4	5	1
恐怖片	1	1	3
爱情片	4	5	1

在数学家看来，这里计算的是五维（而不是二维）空间中的距离，但计算公式不变。 $\sqrt{(a_{1}-a_{2})^{2}+(b_{1}-b_{2})^{2}+(c_{1}-c_{2})^{2}+(d_{1}-d_{2})^{2}+(e_{1}-e_{2})^{2}}$

这个距离公式很灵活，即便设计很多个数字，仍然可以使用它来计算距离。设计5个数字时，距离意味着什么呢？这种距离指出了两组数字之间的相似程度。

张翠山VS宋远桥：\(\sqrt{(3-4)^{2}+(4-3)^{2}+(4-5)^{2}+(1-1)^{2}+(4-5)^{2}}\) = \(\sqrt{1+1+1+0+1}\) = \(\sqrt{4}\) =2
张翠山VS张松溪：\(\sqrt{(3-2)^{2}+(4-5)^{2}+(4-1)^{2}+(1-3)^{2}+(4-1)^{2}}\) = \(\sqrt{1+1+9+4+9}\) = \(\sqrt{24}\) =4.89
上述距离表明，张翠山的喜好更趋近于宋远桥而不是张松溪。

现在要向张翠山推荐电影将易于反掌：只要宋远桥喜欢的电影，就将其推荐给张翠山，反之亦然。这样就创建了一个电影推荐系统。
系统会不断提醒张翠山：多给电影评分吧，评论的电影越多，给张翠山推荐的内容越准确。即评论的电影越多，系统就越能准确的判断张翠山与哪些用户相似。

2.2回归

假设你不仅要向张翠山推荐电影，还要预测她将给这部电影打多少分。为此，先找出与她最近的6个人。
并非一定就是6个最近的邻居，也可选择2个，10个或者10000个。这就是算法名为K最近邻而不是6最近邻的原因
假设你要预测张翠山会给电影廊桥遗梦打多少分。

宋远桥	俞莲舟	俞岱岩	张松溪	殷梨亭
5	4	4	5	3

这些人打算的分数平均值为4.2。这就是回归（regression）。你将使用KNN来做两项基本工作——分类和回归： * 分类就是编组 * 回归就是预测结果（如一个数字）

回归很有用，如你开了个面包店，每天都做新鲜面包，需要根据如下一组特征预测当天该烤多少条面包：

• 天气指数1～5（1表示天气很糟，5表示天气非常好）
• 是不是周末或节假日（周末或节假日为1，否则为0）
• 有没有活动（1表示有，0表示没有）

还有一些历史数据，记录了在各种不同的日子里售出的面包数量。
A：（5，1，0）=300
B：（3，1，1） =225
C：（1，1，0）=75
D：（4，0，1）=200
E：（4，0，0）=150
F：（2，0，0）=50
我们使用K最近邻算法(k-Nearest Neighbor，KNN)，其中的K为4

相似度	当天（4，1，0）
A（5，1，0）	$\sqrt{(4-5)^{2}+(1-1)^{2}+(0-0)^{2}} = \sqrt{1+0+0} =1$
B（3，1，1）	$\sqrt{(4-3)^{2}+(1-1)^{2}+(0-1)^{2}} = \sqrt{1+0+1} =1.41$
C（1，1，0）	$\sqrt{(4-1)^{2}+(1-1)^{2}+(0-0)^{2}} = \sqrt{9+0+0} =3$
D（4，0，1）	$\sqrt{(4-4)^{2}+(1-0)^{2}+(0-1)^{2}} = \sqrt{0+1+1} =1.41$
E（4，0，0）	$\sqrt{(4-4)^{2}+(1-0)^{2}+(0-0)^{2}} = \sqrt{0+1+0} =1$
F（2，0，0）	$\sqrt{(4-2)^{2}+(1-0)^{2}+(0-0)^{2}} = \sqrt{4+1+0} =2.25$

距离最近的为A、B、D、E，将这些天的面包数平均，结果为218.75。这就是今天要烤的面包数。 余弦相似度：前面计算两位用户的距离时，使用的都是距离公式。还有更合适的公式吗？在实际工作中，经常使用余弦相似度。假设有2位品味类似的用户，但其中一位打分时更保守。对于同一部电影，张三给了5星，李四只给了4星。如果你使用距离公式，这两位用户可能不是邻居，虽然他们的品味非常接近。 余弦相似度不计算两个矢量的距离，而比较它们的角度，因此更适合处理前面所说的情况。 ### 2.3挑选合适的特征 * 1.与要推荐的电影紧密相关的特征（给用户一些猫咪的图片打分，这种情况下，你找出的是对小猫图片的欣赏品味类似的用户，而与电影欣赏品味没有多大关系）。 * 2.不偏不倚的特征（例如，如果只让用户给喜剧片打分，就无法判断它们是否喜欢动作片）。

在挑选合适的特征方面，没有放之四海而皆准的法则，你必须考虑到各种需要考虑的因素。

3.机器学习简介

3.1 OCR

OCR是光学字符识别，这意味着你可拍摄印刷页面的照片，计算机将自动识别出其中的文字。Google使用OCR来实现图书数字化。
例如如何快速自动识别出7这个数字？
使用KNN：

• 1.浏览大量的数字图像，将这些数字的特征提取出来。
• 2.遇到新图像时，你提取该图像的特征，再找出它最近的邻居都是谁。

这与前面判断水果是橙子，还是柚子是一样的。
OCR算法提取线段、点和曲线等特征。遇到新字符时，可从中提取出同样的特征。

与前面的水果示例相比，OCR中的特征提取要复杂的多，但再复杂的技术也是基于KNN等简单理念的。这些理念也可用于语音识别和人脸识别。你将照片上穿到Facebook时，它能够自动标出照片中的人物，这是机器学习在发挥作用。

3.2创建垃圾邮件过滤器

垃圾邮件过滤器使用一种简单算法——朴素贝叶斯分类器，首先需要使用一些数据对这个分类器进行训练。

主题	是不是垃圾邮件
重置密码	不是
你中了一百万	是
给我你的密码	是
马云给你一百万	是
生日快乐	不是

例如收到一封“百万大奖待领取”的邮件，这是垃圾邮件吗？ 可以研究这个句子中的每个单词，看看它在垃圾邮件中出现的概率是多少。例如使用这个非常简单的模型时，发现只有词汇百万在垃圾邮件中出现过。朴素贝叶斯分类器能计算出邮件为垃圾邮件的概率，其应用领域与KNN相似。

3.3 预测股票市场

根据以往的数据来预测未来方面，没有万无一失的方法。未来很难预测，由于设计的变数太多，这几乎是不可能完成的任务。

4.小结

• KNN用于分类和回归，需要考虑最近的邻居
• 分类就是编组
• 回归就是预测结果
• 特征抽取意味着将物品（如水果或用户）转换为一系列可比较的数字
• 能否挑选合适的特征事关KNN算法的成败。