9动态规划

1.背包问题

音响3000元4斤
笔记本电脑2000元3斤
吉他1500元1斤
### 1.1.简单算法 最简单的算法：尝试各种可能的商品组合，并找出价值最高的组合。 缺点：速度非常慢。3种商品需要计算8种组合；4件商品是，需要计算16中组合。每增加一种商品，需要计算的集合数将翻倍。这种算法的运行时间为O(2n)
组合1组合2组合3组合4
无吉他音响笔记本电脑
0150030002000
组合5组合6组合7组合8
吉他和音响吉他和笔记本电脑音响和笔记本电脑吉他、音响和笔记本电脑
装不下3500装不下装不下
近似算法可以得到近似解，但不一定是最优解。

2. 动态规划

使用动态规划可以得到最优解。

背包的承重为1斤背包的承重为2斤背包的承重为3斤背包的承重为4斤
吉他1 1500可以放入背包
G 1500		可以放入背包
G 1500		可以放入背包
G 1500		可以放入背包
G 1500
音响4 3000G 1500G 1500G 1500S 3000
笔记本电脑3 2000G 1500G 1500C 20003000 vs (2000+1500) -> 3500
计算公式： cell[i][j] = cell[i-1][j] vs {当前商品的价值 + 剩余空间的价值 = 当前商品的价值+cell[i-1][j-当前商品的重量]}

2.1 实现

bag={
    "computer":{"weight":3,"value":2000},
    "guitar":{"weight":1,"value":1500},
    "sound":{"weight":4,"value":3000}
}
list=[]
goods = []
row=0
def addList(list1,list2):
    for i in list1:
        list2.append(i)
for key in bag.keys():
    sublist=[]
    subGood=[]
    keyWeight = bag.get(key)["weight"]
    keyValue = bag.get(key)["value"]
    for column in range(4):
        sub=[]
        #单元格 = 列的索引+1
        weight = column + 1
        #判断行，行数=0，直接对比；行数大于0，与上一行进行对比
        if(row > 0):
            if(weight < keyWeight):
                sublist.append(list[row-1][column])
                addList(goods[row - 1][column], sub)
            elif(weight == bag.get(key)["weight"]):
                if( list[row-1][column] < keyValue ):
                    sublist.append(keyValue)
                    sub.append(key)
                else:
                    sublist.append(list[row-1][column])
                    addList(goods[row-1][column],sub)
            else:
                #如果单元格重量>商品，就判断商品的权重和同位置大小
                #判断weight-bag.get(key)["weight"]
                if (list[row-1][column] < ( keyValue + list[row-1][weight-keyWeight-1] ) ):
                    sublist.append( keyValue + list[row-1][weight-keyWeight-1])
                    sub.append(key)
                    addList(goods[row - 1][weight-keyWeight-1], sub)
                else:
                    sublist.append(list[row-1][column])
                    addList(goods[row-1][column],sub)
        else:
            #直接判断，单元格 < 物品重量
            if(weight < keyWeight):
                sublist.append(0)
                # sub.append([])
            else:
                sublist.append(keyValue)
                sub.append(key)
        subGood.append(sub)
    list.append(sublist)
    goods.append(subGood)
    row+=1
#最大值肯定在最后一个值
print("4斤背包容纳的最大价值组合：%s %s" % (list[-1][-1],goods[-1][-1]))    #4斤背包容纳的最大价值组合：3500 ['guitar', 'computer']


bag={
    "computer":{"weight":3,"value":2000},
    "guitar":{"weight":1,"value":1500},
    "sound":{"weight":4,"value":3000}
}
list=[]
goods = []
row=0
def addList(list1,list2):
    for i in list1:
        list2.append(i)
for key in bag.keys():
    sublist=[]
    subGood=[]
    keyWeight = bag.get(key)["weight"]
    keyValue = bag.get(key)["value"]
    for column in range(4):
        sub=[]
        #单元格 = 列的索引+1
        weight = column + 1
        #判断行，行数=0，直接对比；行数大于0，与上一行进行对比
        if(row > 0):
            if (weight == bag.get(key)["weight"] and list[row - 1][column] < keyValue):
                sublist.append(keyValue)
                sub.append(key)
            elif(weight > bag.get(key)["weight"] and list[row-1][column] < ( keyValue + list[row-1][weight-keyWeight-1] )):
                sublist.append(keyValue + list[row - 1][weight - keyWeight - 1])
                sub.append(key)
                addList(goods[row - 1][weight - keyWeight - 1], sub)
            else:
                sublist.append(list[row-1][column])
                addList(goods[row - 1][column], sub)

        else:
            #直接判断，单元格 < 物品重量
            if(weight < keyWeight):
                sublist.append(0)
            else:
                sublist.append(keyValue)
                sub.append(key)
        subGood.append(sub)
    list.append(sublist)
    goods.append(subGood)
    row+=1
#最大值肯定在最后一个值
print("4斤背包容纳的最大价值组合：%s %s" % (list[-1][-1],goods[-1][-1]))

3.背包问题FAQ

3.1 增加一个商品时，需要重新执行前面所做的计算吗？

不需要，动态规划逐步计算到最大价值

背包的承重为1斤背包的承重为2斤背包的承重为3斤背包的承重为4斤
吉他1 1500可以放入背包
G 1500		可以放入背包
G 1500		可以放入背包
G 1500		可以放入背包
G 1500
音响4 3000G 1500G 1500G 1500S 3000
笔记本电脑3 2000G 1500G 1500C 20003000 vs (2000+1500) -> 3500
iphone1 2000I 2000 I 2000I G 35003500 vs (2000+2000) -> 4000

3.2 沿着一列往下走，最大价值有可能降低吗？

不可能。每次迭代时，你都存储当前的最大价值。最大价值不可能比以前低。

3.3 行的排列顺序发生变化时结果将如何

答案没有变化。各行的排列顺序无关紧要

3.4 可以逐列而不是逐行填充网格吗

可能有影响

3.5 增加一件更小的商品，将如何呢？

还可以偷一条项链，重0.5斤，价值1000。需要调整网格，将粒度设置为0.5。

3.6 可以偷商品的一部分吗？

没法处理。使用动态规划时，要么考虑拿走整件商品，要么考虑不拿，而没法判断该不该拿走商品的一部分。
但使用贪婪算法可轻松的处理这种情况。首先，尽可能的多拿价值最高的商品；然后拿价值次高的商品，以此类推。

3.7 旅游行程最优化

去伦敦度假，假期2天，没有办法前往每个地方游览。

0.511.52
威斯敏斯特教堂0.5 77777
环球剧场0.5 67131313
英国国家美术馆1 97131622
大英博物馆2 97131622
圣保罗大教堂0.5 8815178+16->24

3.8 处理相互依赖的情况

假设还想去巴黎，因此添加了几项。从伦敦前往巴黎需要0.5天。
如果单独去巴黎的某个景点，每个景点用时1.5天。
到达巴黎后，每个景点用时1天，而不是1.5天。

埃菲尔铁塔1.5天8
卢浮宫1.5天9
巴黎圣母院1.5天7
用动态规划不能对这种情况建模。动态规划能够解决自问题并使用这些答案来解决大问题。仅当每个子问题是离散的，即不依赖于其他子问题时，动态规划才管用。即动态规划解决不了去巴黎玩的问题。

3.9 计算最终的答案时会设计两个以上的子背包吗

根据动态算法的设计，最多只需合并两个子背包，即根本不会设计两个以上的子背包。不过这些子背包可能又包含子背包。即cell[i-1][j-当前商品的重量]可能包含子背包。

3.10 最优解可能导致背包没装满吗？

完全可能

3.11 启示

  • 动态规划可帮助你在给定约束条件下找到最优解。
  • 在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。
  • 每种动态规划解决方案都涉及网格。
  • 单元格中的值通常就是你要优化的值。背包问题中，单元格的值为商品的价值
  • 每个单元格都是一个子问题，因此应考虑将问题分为子问题，这有助于找出网格的坐标轴。

4 最长公共子串与最长公共子序列

最长公共子串是两个字符串中最长的相同字符串。
最长公共子序列是两个字符串中相同的字符数，不需相连，类似动态规划。

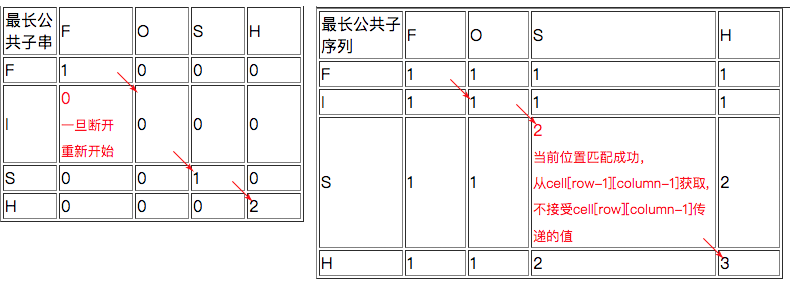
5.动态规划应用

1.生物学家根据最长公共序列来确定DNA链的相似性，进而判断两种动物或疾病有多相似。
2.使用动态规划来比较2个文件的不同，如diff，git

posted on 2020-01-09 21:14  singleSpace  阅读(163)  评论(0)  编辑  收藏  举报

Powered by: 博客园 Copyright © 2024 singleSpace
Powered by .NET 8.0 on Kubernetes