6广度优先搜索
广度优先搜索是图算法。
广度优先搜索让你能够找出两样东西之间的最短距离。最短距离的含义有很多。使用广度优先搜索可以：
- 编写国际跳棋AI，计算最少走多少步就可获胜
- 编写贫血检查器，计算最少编辑多少个地方就可将错拼的单词改成正确的单词
- 根据人际关系网络找到关系最近的医生
1. 图简介
假设要从双子峰前往金门大桥。
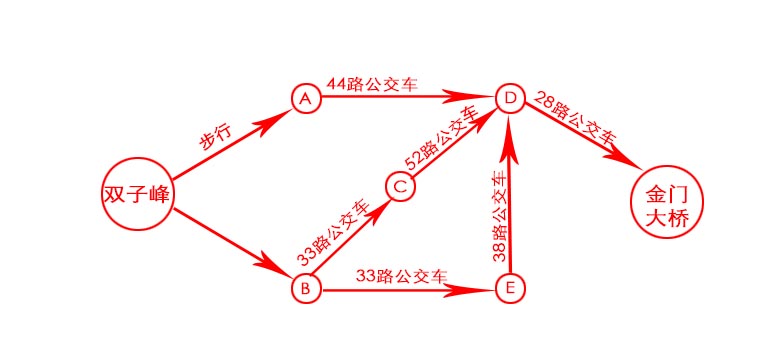
乘公交车前往，并希望换乘最少。
要确定如何从双子峰前往金门大桥，需要两个步骤：
- 使用图来建立问题模型
- 使用广度优先搜索解决问题
对比发现，方法1只需3步。解决最短路径问题的算法被称为广度优先搜索。
| 起点 | 第一步 | 第二步 | 第三步 | |
| 方法1 | A | D | 到达目的地 | |
| 方法2 | B | C | D | 到达目的地 |
| 方法3 | B | E | D | 达到目的地 |
2.图是什么
图模拟一组连接，用于模拟不同的东西是如何相连的。图由节点(node)和边(edge)组成。
一个节点可能与众多节点直接相连，这些节点被称为邻居。
箭头是单向的，称为有向图，其中的关系是单向的，即尾是头的邻居。如果把单向关系视为key-value，即value是key的邻居，key不是value的邻居 ；
无向图没有箭头，直接相连的节点互为邻居。
3.广度优先搜索
广度优先搜索是一种用于图的查找算法，可帮助回答两类问题：
- 问题1:从节点A出发，有前往节点B的路径吗？
- 问题2:从节点A出发，前往节点B的那条路径最短？
3.1 问题1:有路径吗
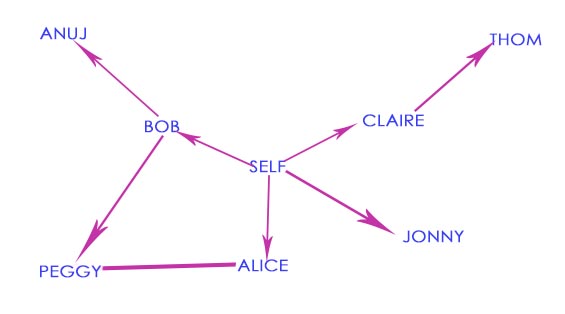
假设你经营者一个芒果农场，需要寻找芒果经销商，以便将芒果卖给他。在Facebook，你与芒果经销商有练习吗？为此，你可在通讯录中查找。
首先创建一个名单，包含了通讯录好友。
然后，依次检查名单中的每个人，看他是否是芒果经销商。
假设你没有朋友是芒果经销商，就必须在朋友的朋友中查找。检查名单的每个人时，你都将其朋友加入名单。
这样一来，你不仅在朋友中查找，还在朋友的朋友中查找。因此如果Alice不是芒果经销商，就将其朋友也加入到名单中。这将意味着你将在她的朋友、朋友的朋友等中查找。使用这种算法将搜遍你的整个人际关系网，直到找到芒果销售商。这就是广度优先算法。
3.2 问题2:查找最短路径
朋友是一度关系，朋友的朋友是二度关系。一度关系胜过二度关系。
应该先在一度关系中搜索，确定其中没有芒果经销商后，才在二度关系中搜索。搜索范围是逐渐向外延伸的。
3.3 队列
队列是一种先进先出的数据结构，而栈是一种后进先出的数据结构。使用队列来控制搜索顺序，避免二度关系搜索先于一度关系搜索执行。
4 实现算法
思路：
- 1.创建一个队列，用于存储要检查的人
- 2.从队列汇中弹出一个人，检查这个人是否芒果经销商
- 3.是，结束执行，返回结果
- 4.不是，将这个人的所有朋友加入队列，回到第2步
from collections import deque
#将所有的朋友添加到数组中
graph=[...]
#使用最后一个字符是否m来判断其是否符合条件
def person_is_seller(name):
return name[-1] == 'm'
def search(name):
#创建一个队列，将你的邻居添加到这个对列中
search_queue = deque()
search_queue += graph["name"]
searched = []
while search_queue: #队列不为空
person = search_queue.popleft() #取出其中的第一个人
if person not in searched:
if person_is_seller(person): #检查这个人是否是芒果经销商
print(person,"是芒果经销商")
return True
else:
search_queue+= graph[person]
searched.append(person) #标记为已检查
return False
这个算法将不断执行，直到满足以下任意一个条件：
- 找到一位芒果经销商
- 对列变成空的，这意味着你的人际关系网中没有芒果经销商。
5 小结
- 广度优先搜索指出是否用从A到B的路径
- 如果有，广度优先搜索将找出最短路径
- 面临类似与寻找最短路径的问题时，可尝试使用图来建立模型，再使用广度优先搜索来解决问题
- 有向图中的边为箭头，箭头的方向置顶了关系的方向，例如key->value，value是key的邻居或key欠value钱。
- 无向图中的边不带箭头，其中的关系是双向的。
- 队列是先进先出的，栈是后进后出的。
- 你需要按加入顺序检查搜索列表中的人，否则找到的就不是最短路径，因此搜索列表必须是队列。
- 对于检查过的人，务必不要再去检查，否则可能导致死循环
