Codeforces Round #409 (rated, Div. 2, based on VK Cup 2017 Round 2) D. Volatile Kite几何

D. Volatile Kite

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a convex polygon P with n distinct vertices p1, p2, ..., pn. Vertex pi has coordinates (xi, yi) in the 2D plane. These vertices are listed in clockwise order.

You can choose a real number D and move each vertex of the polygon a distance of at most D from their original positions.

Find the maximum value of D such that no matter how you move the vertices, the polygon does not intersect itself and stays convex.

Input

The first line has one integer n (4 ≤ n ≤ 1 000) — the number of vertices.

The next n lines contain the coordinates of the vertices. Line i contains two integers xi and yi ( - 109 ≤ xi, yi ≤ 109) — the coordinates of the i-th vertex. These points are guaranteed to be given in clockwise order, and will form a strictly convex polygon (in particular, no three consecutive points lie on the same straight line).

Output

Print one real number D, which is the maximum real number such that no matter how you move the vertices, the polygon stays convex.

Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely, let's assume that your answer is a and the answer of the jury is b. The checker program will consider your answer correct if .

Examples

input

4
0 0
0 1
1 1
1 0

output

0.3535533906

input

6
5 0
10 0
12 -4
10 -8
5 -8
3 -4

output

1.0000000000

Note

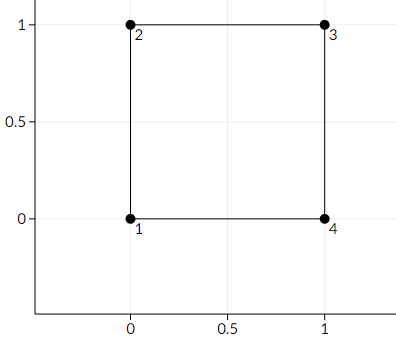
Here is a picture of the first sample

Here is an example of making the polygon non-convex.

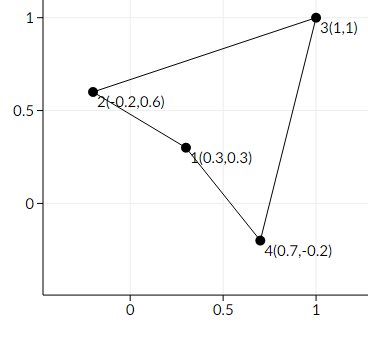
This is not an optimal solution, since the maximum distance we moved one point is  ≈ 0.4242640687, whereas we can make it non-convex by only moving each point a distance of at most  ≈ 0.3535533906.

题目大意：给你一个凸n边形，你可以移动每个点在m范围之内，问你m最大为多少时，这个n边形仍为凸边形。

题目解析：当一个点A和它相连的两个点B、 C退化为成一条直线的时候就不满足题意了。

　　　　　所以呢，这三个点分别画圆，半径为m，然后一条直线可以切过这三个圆。

              然后这个最小的切线就是答案。

              如果你画个图可以发现，这三个点组成的三角形，其中点A到BC的距离为2R = 2m

              所以求出这个三角形的高h/2就好了嘛

#include <bits/stdc++.h>

using namespace std;
const int MAXN = 2007;
const double EPS = 1e-10;

double add(double a, double b) {
    if(abs(a+b) < EPS*(abs(a) + abs(b))) return 0;
    return a+b;
}
struct P {
    double x, y;
    P() {}
    P(double x_, double y_):x(x_), y(y_) {}
    P operator + (P p) {
        return P(add(x, p.x), add(y, p.y));
    }
    P operator - (P p) {
        return P(add(x, -p.x), add(y, -p.y));
    }
    P operator * (double d) {
        return P(x*d, y*d);
    }
    double dot(P p) {
        return add(x*p.x, y*p.y);
    }
    double det(P p) {
        return add(x*p.y, -y*p.x);
    }
} s[MAXN];
bool on_seg(P p1, P p2, P q) {
    return (p1 - q).det(p2 - q) == 0 && (p1 - q).dot(p2 - q) <= 0;
}
double dist(P p1, P p2) {
    return sqrt( (p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y) );
}

int main() {
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        scanf("%lf%lf", &s[i].x, &s[i].y);
    }
    for(int i = n+1; i <= 2*n; i++){
        s[i] = s[i-n];
    }
    double ans = 1e18;
    for(int i = 1; i <= n; i++){
        double tmp = (s[i+2] - s[i]).det(s[i+1] - s[i])/2;
        ans = min(ans, tmp/dist(s[i], s[i+2]));
    }
    printf("%.10f\n", ans);
    return 0;
}