【剑指 Offer】004. 二维数组中的查找

题目描述

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例
现有矩阵 matrix 如下：

[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5，返回 true。
给定 target = 20，返回 false。

限制
0 <= n <= 1000
0 <= m <= 1000

方法一：暴力遍历

若使用暴力法遍历矩阵 matrix ，则时间复杂度为 O(NM)

方法二：二叉搜索树

将示例逆时针旋转 45° ，发现会类似二叉搜索树，这样利用二叉搜索树的思想，O(M+N) 能找到。

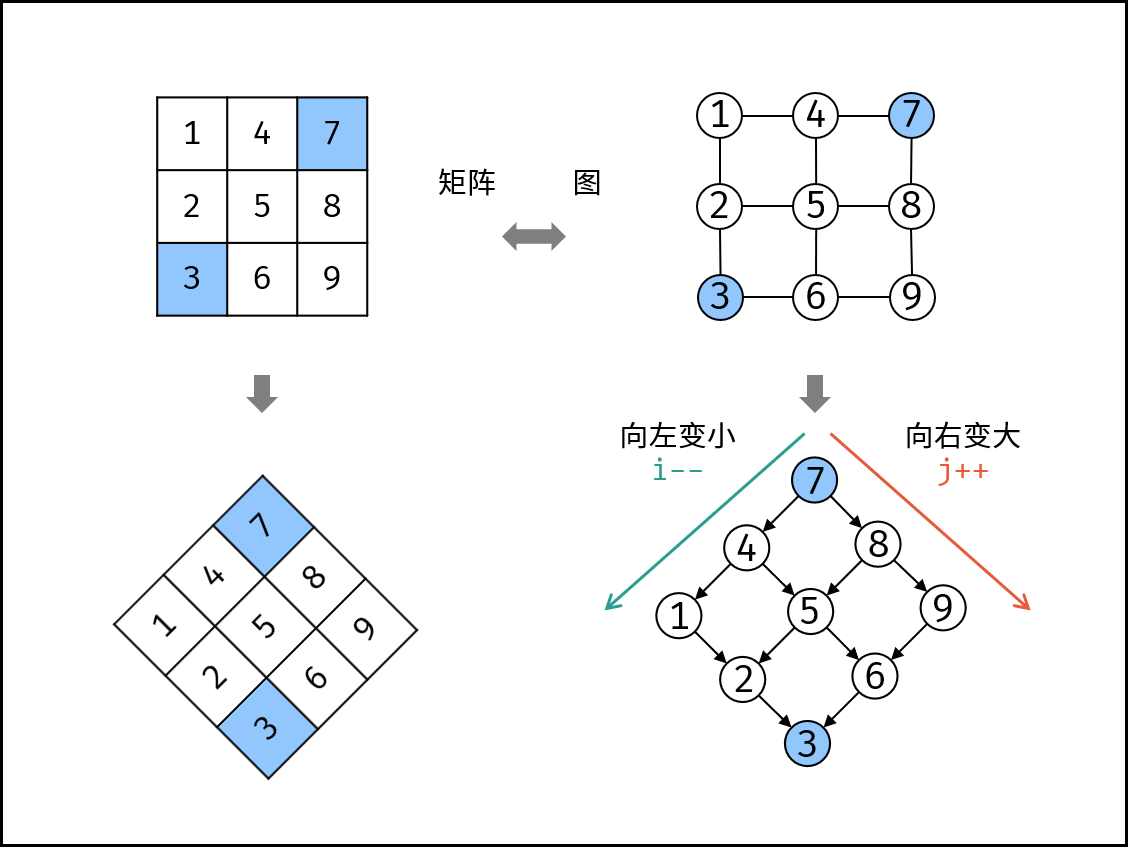
实际上不仅可以以右上角为树的顶点，左下角也可以。

// c++
// 线性时间，O(M+N)，利用类似于二叉树的性质
bool findNumberIn2DArray(vector<vector<int>> &matrix, int target)
{
    if (matrix.size() <= 0)
        return false;
    
    int row = 0;    // 索引
    int column = matrix[0].size() - 1;      // 索引

    while (row < matrix.size() && column >= 0)
    {
        if( target > matrix[row][column])
            row++;
        else if (target < matrix[row][column])
            column--;
        else
            return true;
    }
    return false;
}

// python3
def findNumberIn2DArray(matrix: List[List[int]], target: int) -> bool:
    if len(matrix) == 0:
        return False
    row = 0
    column = len(matrix[0]) - 1

    while (row < len(matrix)) and (column >= 0):
        if target > matrix[row][column]:
            row += 1
        elif target < matrix[row][column]:
            column -= 1
        else:
            return True
    return False