ACwing 最短路算法
ACwing 最短路算法
首先介绍一下各个最短路算法的分类及适用情况
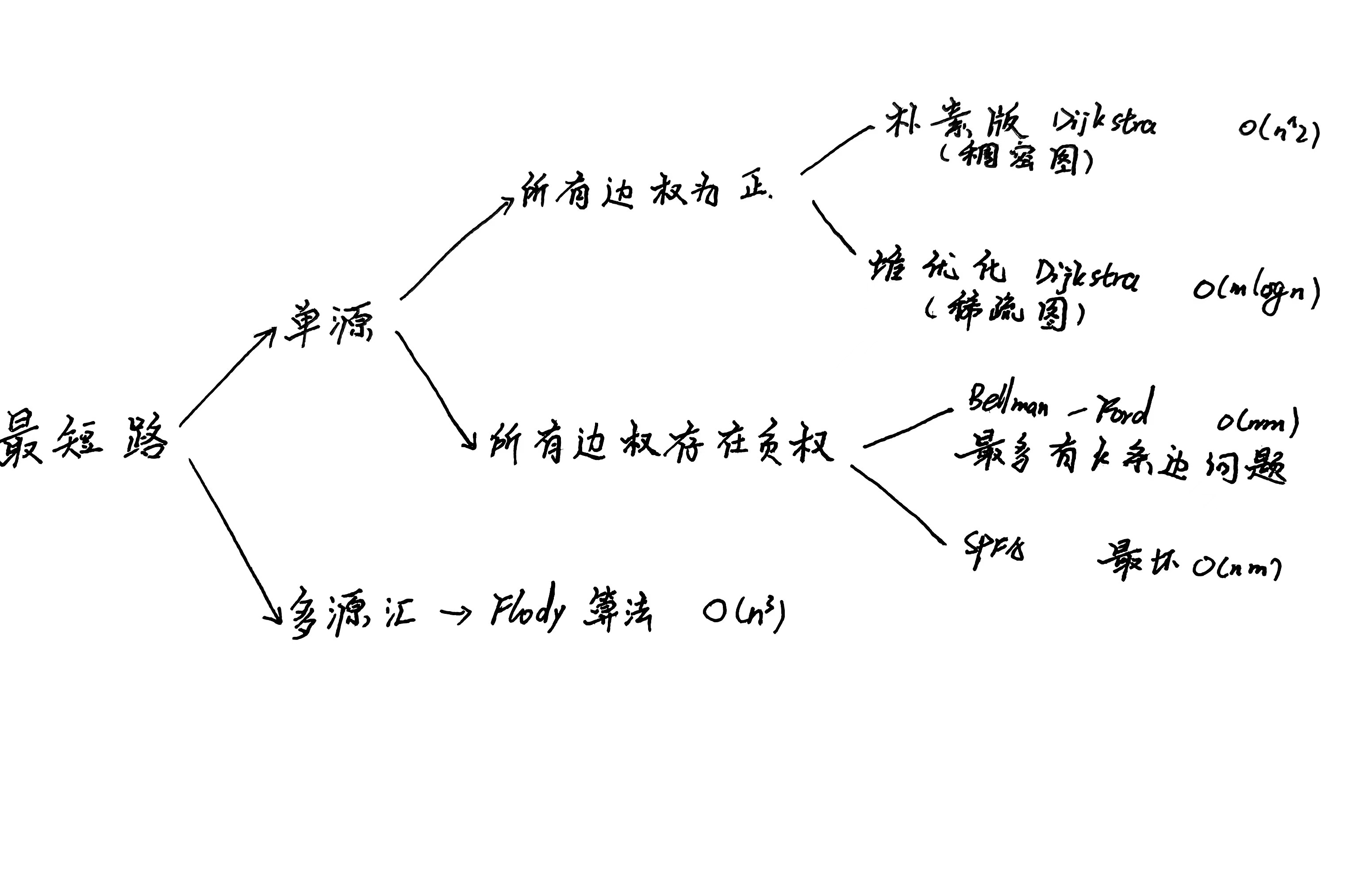
注意:SPFA算法在部分情况下会被卡一些特殊数据,当被卡时,换用其他对应的算法;
下面依次介绍:
朴素版dijkstra算法
朴素版dijkstra算法适用于稠密图,所以我们只以稠密图的存图方式去介绍;
核心思想:
首先我们定义一个集合st用来储存已经确定从起点到这个点的最短路径的点,比如我们以1为起点,那么1到起点的最短路径就已经确定了,就是0,所以我们就将1放入st集合;
如下图,绿色圈表示在集合st中:
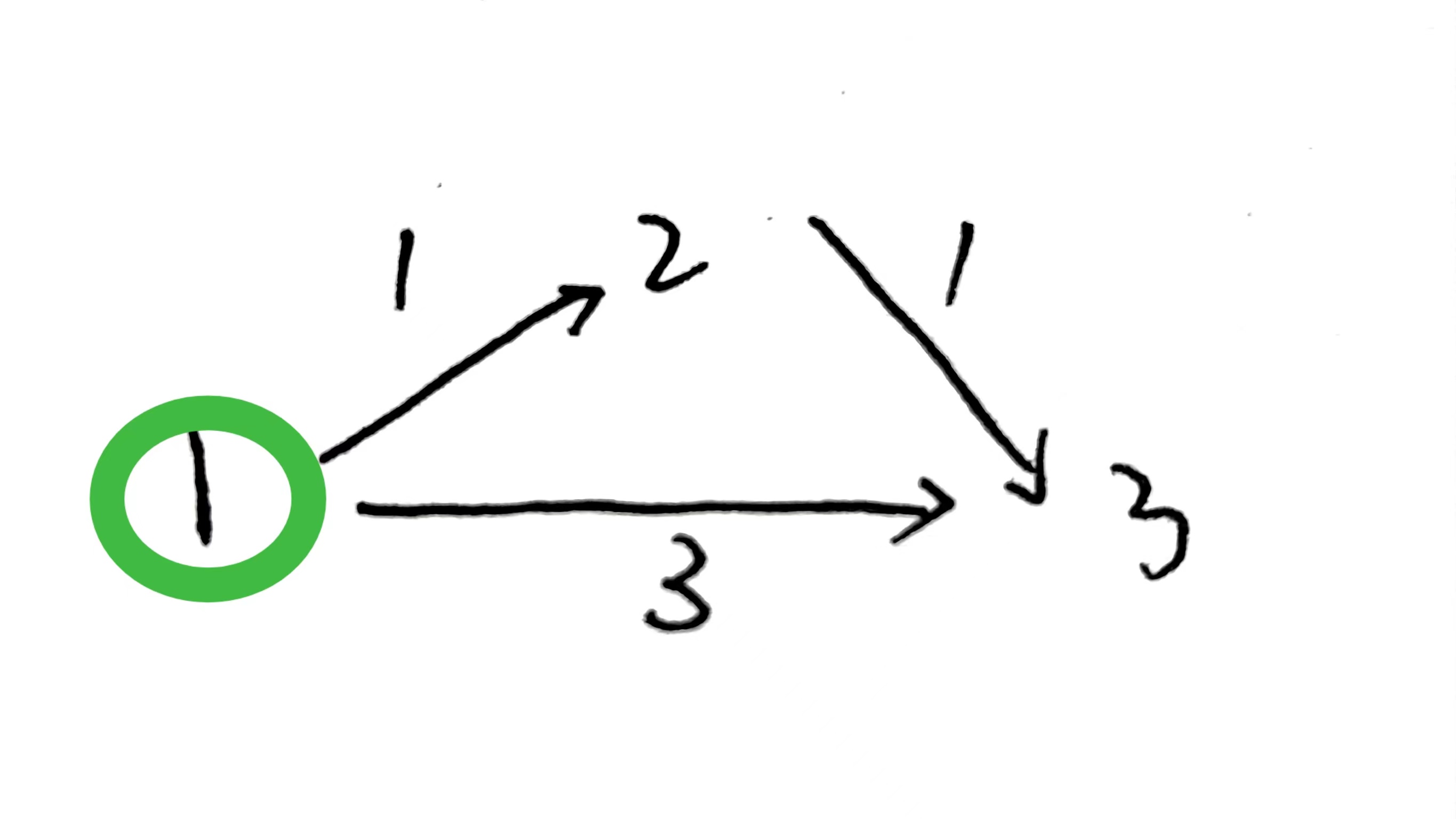
然后我们去寻找距离起点最近的点,发现2距离起点的距离最近,那么我们就将2加入到st集合中
然后将2能够到达的所有点距离起点的距离更新,比如2能够到达3,那么3的距离就更新为2;
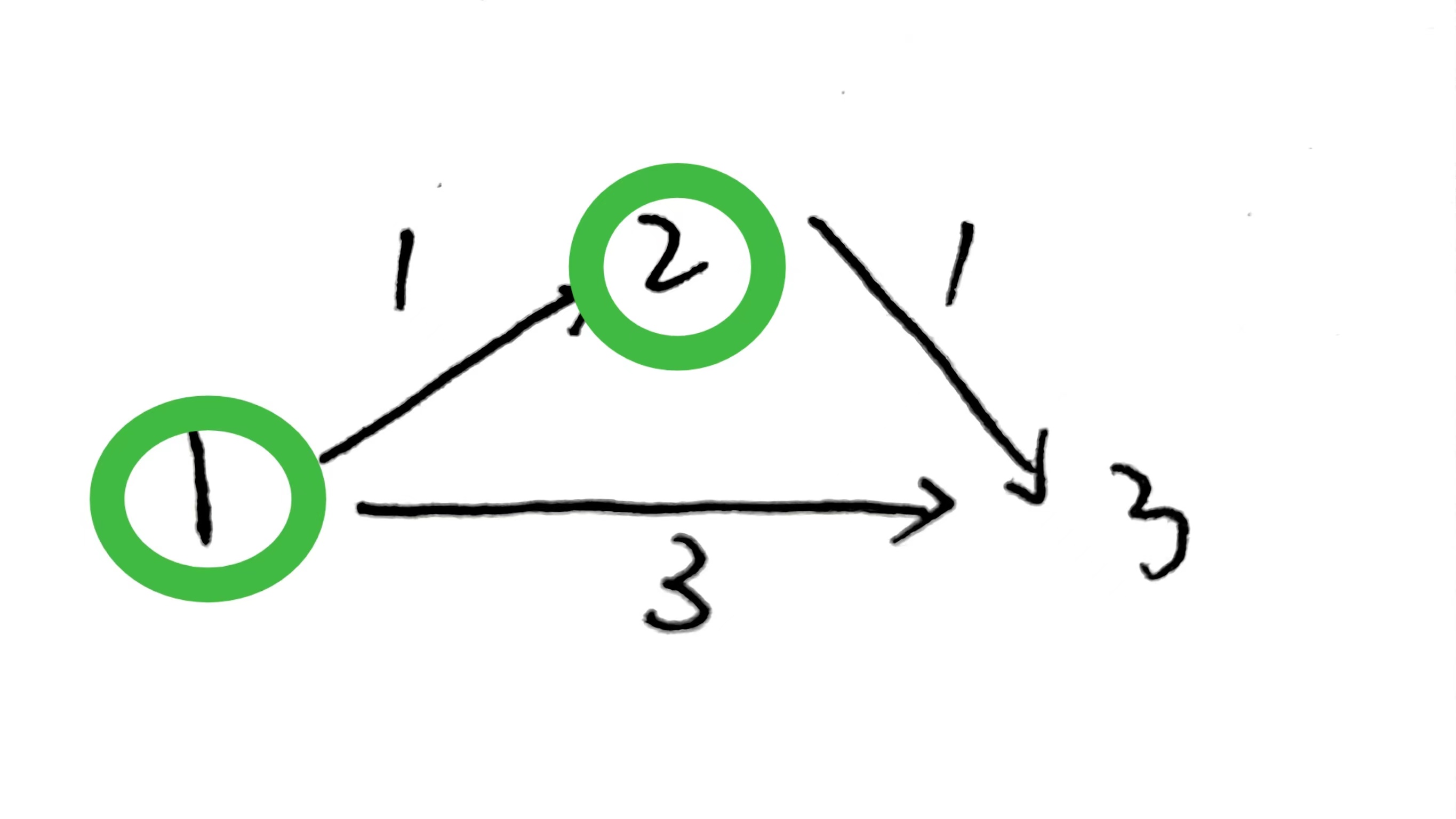
继续寻找距离起点最近的点,依次放入3,4,并更新距离;
下面解释这种方式的原理:
上述过程中,我们反复寻找的是距离起点最近的点,那么刚开始的时候,我们放入集合中的点就是距离起点最近的点(假设为x),很显然x的最短路就是它距离起点的距离;
然后我们用x去更新x能到达的所有点的距离,然后反复寻找。这样每次距离起点的最近的点的最短路已经确定,因为如果使用其他路径的话,就会产生绕路。
然后看代码:
int n, m;
const int N = 510;
int g[N][N];//用来储存图
bool st[N];//st集合
int dist[N];//储存距离
void dijkstra()
{
memset(dist, 0x3f, sizeof(dist));//将所有距离初始化为无穷大
dist[1] = 0;
for (int i = 0; i < n - 1; i++)//循环n-1次,每次向集合中放入一个数,n-1就已经放入所有数
{
int t = -1;//
for (int j = 1; j <= n; j++)
{
if (!st[j] && (t == -1 || dist[t] > dist[j]))//如果不在集合中,并且距离最小,就更新
{
t = j;
}
}
//点t放入st数组
st[t] = true;
for (int j = 1; j <= n; j++)//更新其他点距离
{
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
}
if (dist[n] == 0x3f3f3f3f) cout << -1 << endl;//没找到
else cout << dist[n] << endl;
}
int main()
{
memset(g, 0x3f, sizeof(g));//将图中所有点初始化为无穷大
cin >> n >> m;
while (m--)
{
int x, y, z;
cin >> x >> y >> z;
g[x][y] = min(g[x][y], z);//如果有重边的话,我们就取最短的就好
}
dijkstra();
return 0;
}
堆优化版dijkstra
将朴素版的各个操作使用堆来实现,用于稀疏图:
int n, m;
const int N = 1000005;
int e[N], ne[N], h[N], idx, w[N];//稀疏图使用链表来存
bool st[N];
int dist[N];
void add(int x, int y, int z)//默写
{
e[idx] = y;
ne[idx] = h[x];
h[x] = idx;
w[idx++] = z;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
priority_queue < pair<int, int>, vector < pair<int, int> >, greater<pair<int, int>>> heap;//优先队列{当前点路径距离,点}
heap.push({ 0,1 });//将{0,1}压入
while (heap.size())//当堆不为空,堆不为空时,那么说明上一次没有找到距离起点最近的点,说明已经找完所有点,或者无路可走
{
auto t = heap.top();//取出堆顶
heap.pop();//删除堆顶
int ver = t.second, distance = t.first;
if (st[ver]) continue;//查看是否在st数组中
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])//遍历ver所能到达的所有点
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])//如果出现更小的距离,就更新距离
{
dist[j] = dist[ver] + w[i];
heap.push({ dist[j],j });//将更新距离的点压入堆
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main()
{
memset(h, -1, sizeof(h));//注意将h数组全部初始化为-1
cin >> n >> m;
while (m--)
{
int x, y, z;
cin >> x >> y >> z;
add(x, y, z);
}
cout << dijkstra()<<endl;
return 0;
}
bellman_ford算法
bellman_ford算法主要用于求有边数限制的最短路,和求是否有负环(一般效率差于SPFA,但是是SPFA被卡时的保底算法);
核心思想:
限制最短路一共有k条边,那么就循环k次,每一次就所有点向外延伸一条边;
实现所有点向外延伸一条边,就遍历所有边,将可以走的边走一遍;
代码如下:
int n, m,k;
const int N = 510;
int dist[N], backup[N];
const int M = 10005;
struct edge//bellman_ford算法要求我们只要可以遍历所有边就行,所以使用结构体去储存所有边比较简单
{
int x;
int y;
int w;
}edges[M];
void bellman_ford()
{
memset(dist, 0x3f, sizeof(dist));//常规初始化
dist[1] = 0;
for (int i = 0; i < k; i++)//循环K次,所有点向外延伸k次
{
memcpy(backup, dist,sizeof(dist));//做一个备份,保证后面循环时每一个点只向外延伸一次
for (int j = 0; j < m; j++)
{
auto e = edges[j];
dist[e.y] = min(dist[e.y], backup[e.x] + e.w);//更新距离
}
}
//因为循环时是所有点同时走,所以就算终点无法到达,终点的距离也会改变,所以用0x3f3f3f3f/2限制一下
if (dist[n] > 0x3f3f3f3f / 2) cout << "impossible" << endl;
else cout << dist[n] << endl;
return;
}
int main()
{
cin >> n >> m>>k;
for (int i = 0; i < m; i++)
{
cin >> edges[i].x >> edges[i].y >> edges[i].w;
}
bellman_ford();
return 0;
}
另外介绍bellman_ford算法判断负环的方式;
if (dist[e.y] > backup[e.x] + e.w)//如果绕路的距离比直接走短,那么说明这个点的最短路上多了1个点
{
dist[e.y] = backup[e.x] + e.w;
cnt[e.y] = cnt[e.x] + 1;//点数等于前置点+1
if (cnt[e.y] >= n) return true;//因为一共n个点,如果没有负环的话,那么走到终点一共最多n-1条边
//如果出现了cnt>=n,那么与上述逻辑违背,说明有负环存在
}
SPFA算法(99.9%的题都可以解决)
SPFA的算法逻辑与bfs十分相似,都是先找第一层,然后第二层......SPFA实际上是对bellman_ford算法进行优化,
在bellman_ford算法中,我们遍历所有边做如下的操作:
dist[e.y] = min(dist[e.y], backup[e.x] + e.w);//更新距离
但是不是所有的点都会更新,只有当我的backup[e.x] 变小的时候,dist[e.y]才会被更新,那么我们每次遍历所有backup[e.x]变小的点就好了;
所以我们使用宽搜进行优化;
int n, m;
const int N = 100005;
int h[N], e[N], ne[N], idx, w[N];
bool st[N];
int dist[N];
void add(int x, int y, int z)
{
e[idx] = y;
ne[idx] = h[x];
h[x] = idx;
w[idx++] = z;
}
void spfa()
{
queue<int > q;
q.push(1);
memset(dist, 0x3f, sizeof(dist));//常规初始化
dist[1] = 0;
st[1] = true;//st数组此时表示一个点是否在队列中
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])//遍历这个点的下一层
{
int j = e[i];
if (dist[j] > dist[t] + w[i])//如果这个点的距离被更新了,也就是上面说的backup[e.x]
{
dist[j] = dist[t] + w[i];
if (!st[j])//如果这个点不在队列中就加进去
{
q.push(j);
st[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) cout << "impossible" << endl;
else cout << dist[n] << endl;
}
int main()
{
memset(h, -1, sizeof(h));
cin >> n >> m;
while (m--)
{
int x, y, z;
cin >> x >> y >> z;
add(x, y, z);
}
spfa();
return 0;
}
唯一多源最短路算法floyd算法
floyd算法一共有三层循环,第一层循环,枚举所有中转点,第二层枚举所有起点,第三层枚举所有终点;
此时从起点到终点的路有两种,一种是从起点直接到达终点,一种是从起点到达中转点,然后再从中转点到达终点,然后取两种路距离的最短值;
int n, m, k;
const int N = 205;
int dist[N][N];
void floyd()
{
for (int h = 1; h <= n; h++)//枚举中转点
{
for (int i = 1; i <= n; i++)//枚举起点
{
for (int j = 1; j <= n; j++)//枚举终点
{
//经过中转点的距离为dist[i][h]+dist[h][j],从i到h的距离加上从h走到j的距离
dist[i][j] = min(dist[i][j], dist[i][h] + dist[h][j]);
}
}
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (i == j) dist[i][j] = 0;
else dist[i][j] = 0x3f3f3f3f;
}
}
//初始化距离
while (m--)
{
int x, y, z;
cin >> x >> y >> z;
dist[y][x] = dist[x][y] = min(dist[x][y], z);//多条边取最短
}
floyd();
while (k--)
{
int x, y;
cin >> x >> y;
if (dist[x][y] >= 0x3f3f3f3f / 2)cout << "impossible" << endl;
else cout << dist[x][y] << endl;
}
return 0;
}
建图细节
建图的细节点就在重边和自环,
当我们用链表存储图时,那么有重边和自环就不需要取考虑了,记得将h数组初始化为-1
但是当我们使用二维数组去存图时,就需要去特殊考虑
如果没有自环,采取如下初始化方式;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (i == j) dist[i][j] = 0;//将自环情况改为0
else dist[i][j] = 0x3f3f3f3f;//其余初始化为0x3f3f3f3f
}
}
如果有自环,如下
memset(g,0x3f,sizeof(g));
如果有重边,就在输入时处理
dist[i][j] = min(dist[i][j],w);
如果无向图
dist[i][j] = dist[j][i] = w;


