PTA-第三次机考题解
PTA-第三次机考题解
7-1 玩游戏一
典型的二分模版题，之前发的第十一次练习题目中对二分有详细的讲解，这道题就是二分的第二种模版，原封不动。相信认真看过的同学还是有思路的。嘿嘿！
给没有看过的同学下面再讲一次二分：
直接讲整数二分，浮点数二分只需要修改细节就好（直接讲两种模版，所有的二分都是这种模版）
1.
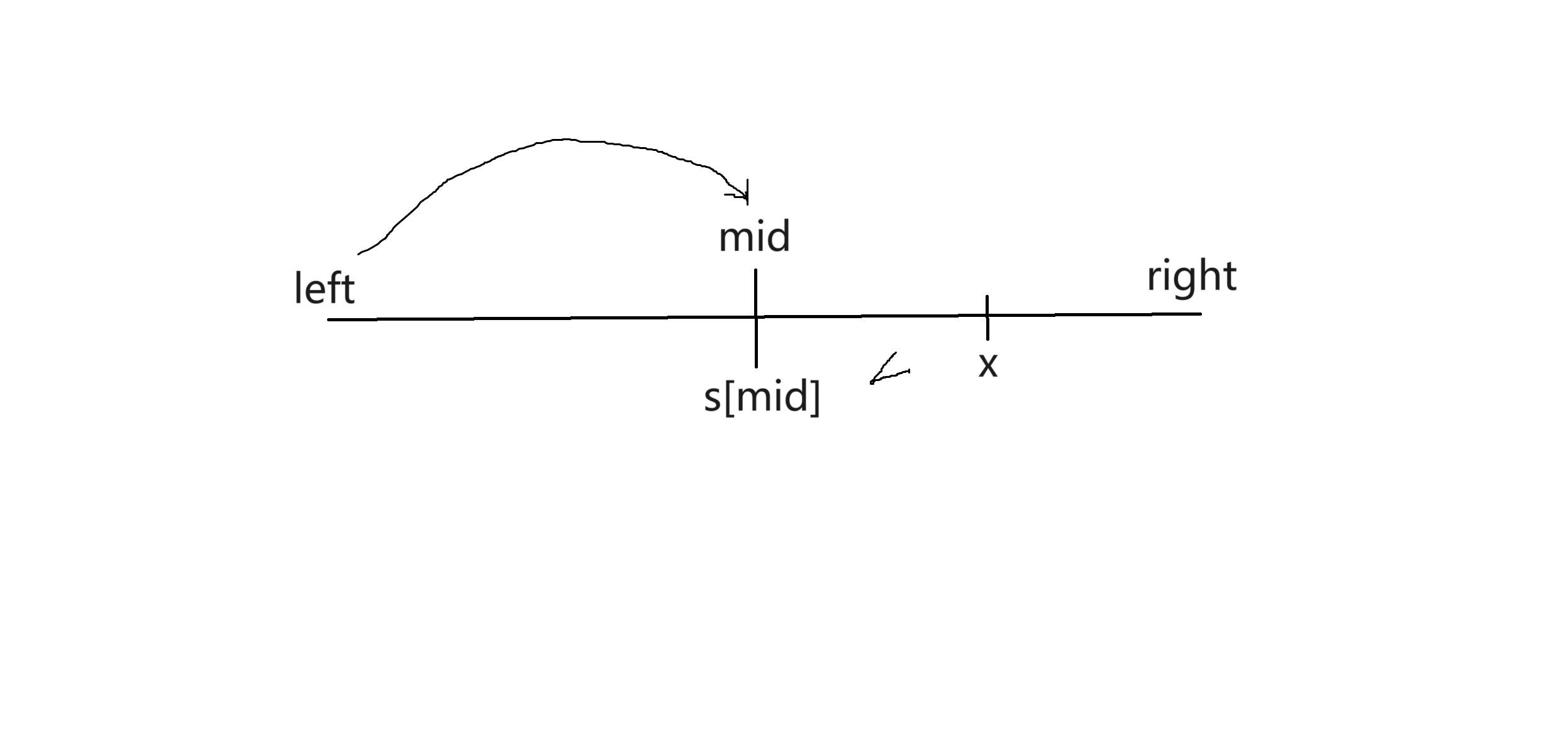
每次找到区间的中点，将s[mid]与x的值相比较。如果是图中的这种情况，x>s[mid] ，所以x存在于右区间。那么调整区间，将区间的左端点调整为mid+1（为什么是mid+1后面会讲），再去循环处理右区间。另一种情况同理。
2.
因为存在边界问题，所以这里的二分需要分情况讨论，对应的代码也有两种。
首先是边界调整的问题。重要的就是那边可以取到最后的值x，就将哪边的边界调整为mid。直接看代码讲。(代码题目是找到x在数组中的位置)
先看第一种：
int l = 0,r = n-1//设置左右端点
while(l<r)
{
int mid = l+r>>1;//设置中点
if(s[mid]>=x) r = mid;
//注意此时x可以在这个判断条件中取到，所以这个条件对应的边界调整为mid
else l = mid+1;
//另一个对应的调整为mid+1或mid-1；
}
第二种：
int l = 0,r = n-1;
while(l<r)
{
int mid = l+r+1>>1;
if(s[mid]<=x) l = mid;
//这时x可以在新的条件中取到，所以对应边界调整为mid,其余同理。
else r = mid-1;
}
3.
另外的，两种情况所移动的方向不同。
当用第一种模版时，将会从数组左向右去找x的值，直到从左向右找到第一个数为止，此时的边界l就是第一个x的位置。
当用第二种模版时，将会从右向左，直到找到一个数为止，l代表找到的第一个x的位置,注意使用这个模版时，mid = l+r+1>>1。
以上就是二分的两种模版。
那么对于这道题，要求的是求每个战士可以补充能量的最大值，那么可以设置最少的能量值是0，最大的能量值是数组当中最大的元素（每个战士获得的能量不可能超过这个max）。
那就得到了l和r的初始值，
int l = 0, r = max;
然后就是套用模版，
在模版的选择上，因为满足条件的值总在左端取到，所以选择第二种模版。
while (l < r)
{
int mid = l+r+1 >> 1;//注意此时mid = (l+r+1)/2;
if (check(mid)) l = mid;//如果满足条件，说明此时每个战士能量值太小了，就将左边界调整为mid
else r = mid-1;//同理将右边界调整为mid-1
}
下面是check(int x) 函数，作用是用来判断是否每个战士都可以得到能量值x，如果可以就返回true,否则就返回false;
//check函数
//就是判断每个a[i]中含有几个x，将个数相加，看和战士数（m）的大小
//如果个数大于m,说明这个能量值是满足条件的，就返回true，否则就返回false
bool check(int x)
{
int sum = 0;
for (int i = 0; i < n; i++)
{
sum += a[i] / x;
}
if (sum >= m) return true;
else return false;
}
以下是完整代码：
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdbool.h>
int a[10010];
int n, m;
bool check(int x)
{
int sum = 0;
for (int i = 0; i < n; i++)
{
sum += a[i] / x;
}
if (sum >= m) return true;
else return false;
}
int main()
{
scanf("%d %d", &n, &m);
int max = -2e9;
for (int i = 0; i < n; i++)
{
scanf("%d", &a[i]);
max = a[i] > max ? a[i] : max;
}
int l = 0, r = max;
while (l < r)
{
int mid = l+r+1 >> 1;
if (check(mid)) l = mid;
else r = mid-1;
}
printf("%d\n", l);
return 0;
}
6-4 字符串重组
想问没过的同学们，你们新字符串后面＋‘\0’了么，最后使用%s输出的哦，不然就会烫烫烫了。/ww
下面看题：
首先我们定义一个数组s用来储存拼接之后的字符串，另外设置指针k指向s数组，指针m指向str1数组。
char s[128];//储存新字符串
int k = 0,m = 0;
我们用循环来遍历一遍str2数组
用x储存str2[i]表示的数，然后将st1中的x个字符储存到新字符数组中，最后将str2[i]储存到新数组中。
for (int i = 0;str2[i]!='\0'; i++)//如果str2[i] == '\0'说明字符串结束，结束循环
{
int x = str2[i] - '0';//储存str2[i]表示的数
for (int j = 0;j<x; j++)
{
s[k++] = str1[m++];//将st1中的x个字符储存到新字符数组
}
s[k++] = str2[i];//最后将str2[i]储存到新数组中
}
然后考虑一种情况，如果str2循环完毕，但是str1还没有循环完毕。
这时我们需要把str1剩余的字符储存到新字符串中。
while (str1[m]!='\0') s[k++] = str1[m++];
最后将新数组储存会原数组就好。
for (int i = 0; i < k; i++)
{
str1[i] = s[i];
}
注意注意注意：+++++++'\0'
我真的哭死，不加'\0'就会输出乱码，当时卡我好久。
因为最后输出时，主函数使用的是%s,所以我们必须加一个'\0'表示字符串结束。
str1[k] = '\0';
以下是完整代码：
void recombination(char str1[], char str2[])
{
char s[128];
int k = 0,m = 0;
for (int i = 0;str2[i]!='\0'; i++)
{
int x = str2[i] - '0';
for (int j = 0;j<x; j++)
{
s[k++] = str1[m++];
}
s[k++] = str2[i];
}
while (str1[m]!='\0') s[k++] = str1[m++];
for (int i = 0; i < k; i++)
{
str1[i] = s[i];
}
str1[k] = '\0';
}
6-2 麦卡锡函数
这道题的递归方式，题目中已经给出，我们只需要注意输出方式就好了。
int m91(int n)
{
printf("%d ", n);//先把当前的n输出
if (n > 100) //按照题意递归
{
return n - 10;
}
else
{
return m91(m91(n + 11));
}
}
6-1 数组逆序
将第一个数与倒数第一个数交换，第二个数与倒数第二个数交换.......以此类推。
void reverseArray(int array[], int size)
{
for (int i = 0; i < size / 2; i++)
{
int x = array[i];
array[i] = array[size - 1 - i];
array[size - 1 - i] = x;
}
}
6-3 矩阵校验
懒了。。。。。直接解释一下官方的代码。
void check(int matrix[][LEN], int sum_row[], int sum_col[], int rows, int cols)
{
int err_i = -1, err_j = -1;//err_i储存错误数据的行数，err_j同理
for (int i = 0; i < rows; ++i)
{
int sum = 0;
//计算每一行的和
for (int j = 0; j < cols; ++j)
{
sum += matrix[i][j];
}
//判断是否与输入值相等
if (sum != sum_row[i])
{
err_i = i;
}
}
for (int i = 0; i < rows; ++i)
{
int sum = 0;
for (int j = 0; j < cols; ++j)
{
sum += matrix[j][i];
}
if (sum != sum_col[i])
{
err_j = i;
}
}
}
完结！
