PTA-2023第十一次练习题目讲解
PTA-2023第十一次练习题目
以下代码已做防抄袭处理，切勿抄袭。
注意：手机端因为屏幕限制，代码会有（不希望的）换行。解决方案：1.建议使用电脑端打开。2.点击代码进入全屏观看。
6-17 实验7_9_简单排序
法一：冒泡排序
上课学过好多好多次，讲解略过，代码有注释。
void bubbleSort(int data[],int elementCount)
{
for(int i = 0;i<elementCount-1;i++).//第一层循环，控制找最大值的次数
{
for(int j = 0;j<elementCount-1;j++)//第二层循环，每次找到一个最大值
{
if(data[j]>data[j+1]) //如果前一个数大于后一个数，就交换两个数
{
int x = data[j];
data[j] = data[j+1];
data[j+1] = x;
}
}
}
}
以下的几种排序方式，函数需要的接口与这道题提供的函数接口不相同，所以需要重新设置函数接口，这里不讲，我们只讲排序思路。
法二：快速排序（分治思想）
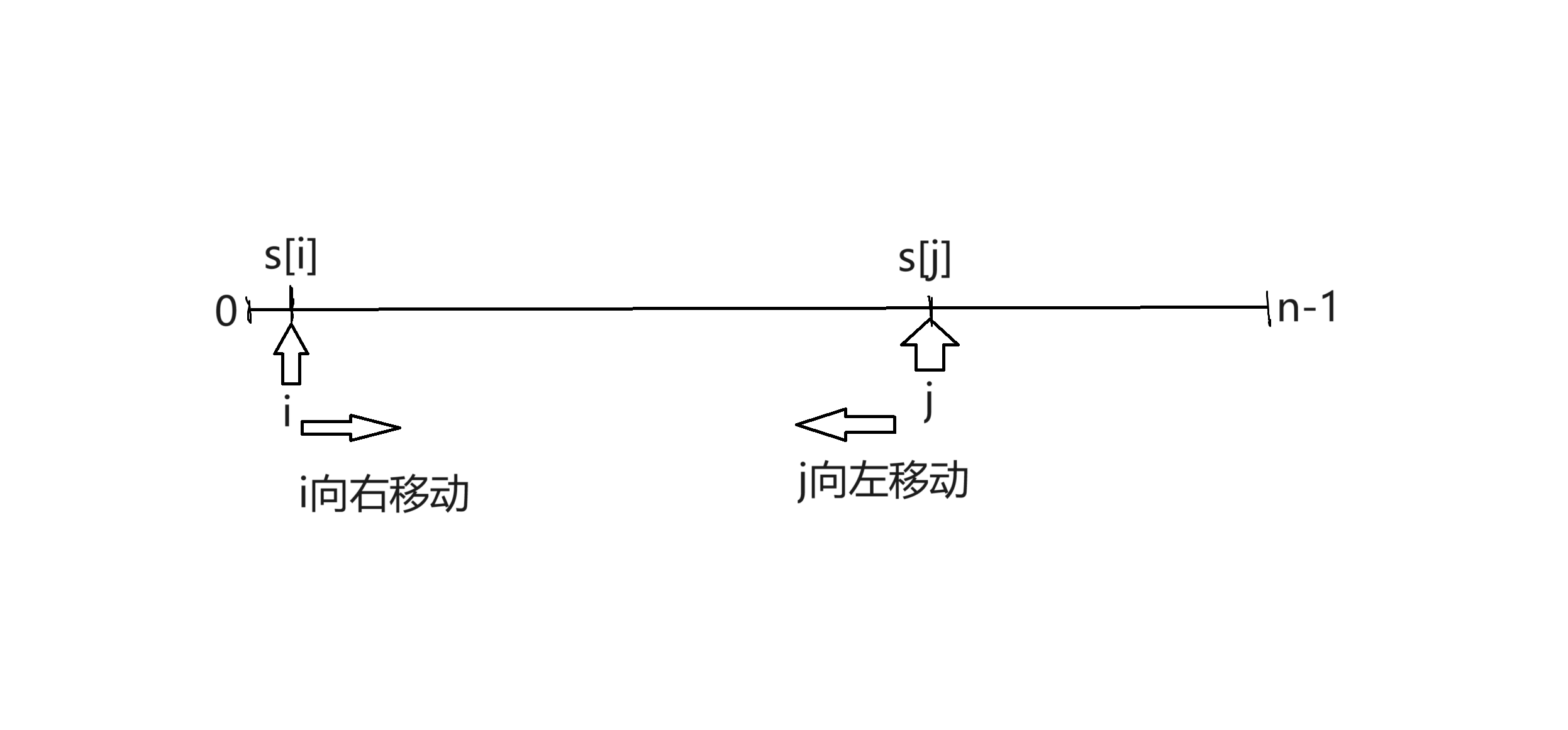
主体思路：定义一个数x属于数组s，利用双指针，将数组分为大于等于x和小于等于x的两部分，然后递归处理。（具体步骤如下）
1.
如上图所示，我们定义一个数组s用来储存n个数据，然后定义两个指针i j,分别指向数组的左右两端，同时i指针逐个向右移动扫描数组，j指针同理向左。
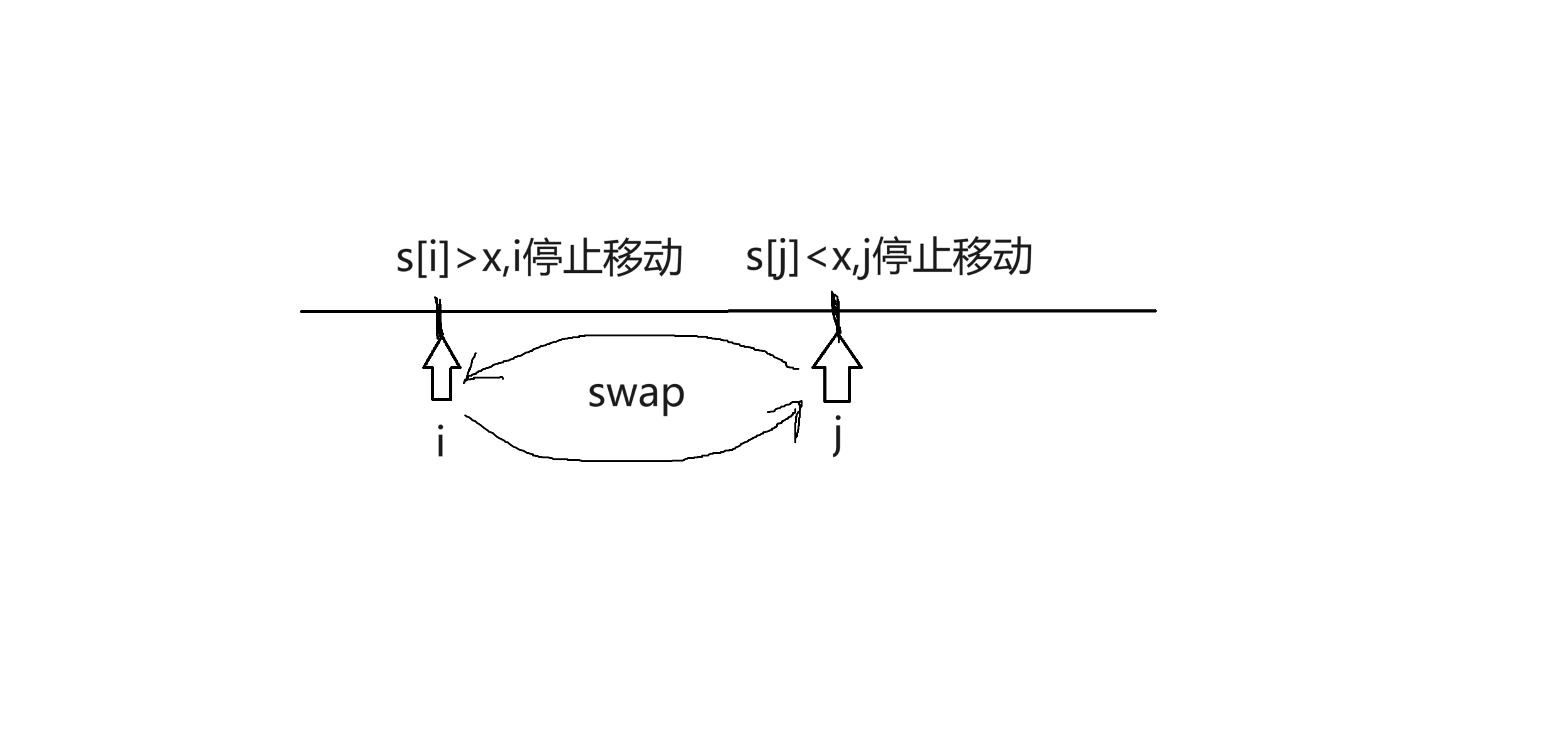
2.
当i,j指针扫描的过程中，当s[i]>x时，指针i就停止移动，同理当s[j]<x时，指针j就停止移动，然后交换s[i]与s[j]，那么就使得大于x的s[i]去到了右边的数组，小于x的s[j]去到了左边的数组。
while(i<j)
{
do i++;while(s[i]<x);//i指针向右移动，当s[i]>x,移动停止，j同理
do j--;while(s[j]>x);
if(i<j)swap(s[i],s[j]);//如果i<j说明s[j]<x<s[i],就进行交换
}
3.
重复以上操作，直到i>=j为止。然后相同的方式利用递归处理左右两半边的数组，直到子数组长度等于1。
quick_sort(s,l,j);
quick_sort(s,j+1;r);
完整代码如下
int n;
int s[1000010];
void quick_sort(int s[], int l, int r)//将s[]数组的l-r区间内的数据排序
{
if (l >= r)return;
//以中点数据值作为分界值，避免边界问题。
//注意：以s[l],s[r]作为分界值时需要考虑边界问题，所以直接取中点値
int x = s[l + r >> 1], i = l - 1, j = r + 1;
while (i < j)
{
do i++; while (s[i] < x);//指针移动直到遇到不符合条件的值
do j--; while (s[j] > x);
if (i < j)swap(s[i], s[j]);//交换两值
}
quick_sort(s, l, j);.//递归处理左右两边
quick_sort(s, j + 1, r);
}
法三：归并排序（分治思想）
主体思路：将数组均分为两半部分，分别有序化，然后合并两个数组
1.
将数组均分为两半部分，利用递归分别有序化。
int mid = l+r>>1;
merge_sort(s,l,mid);
merge_sort(s,mid+1,r);
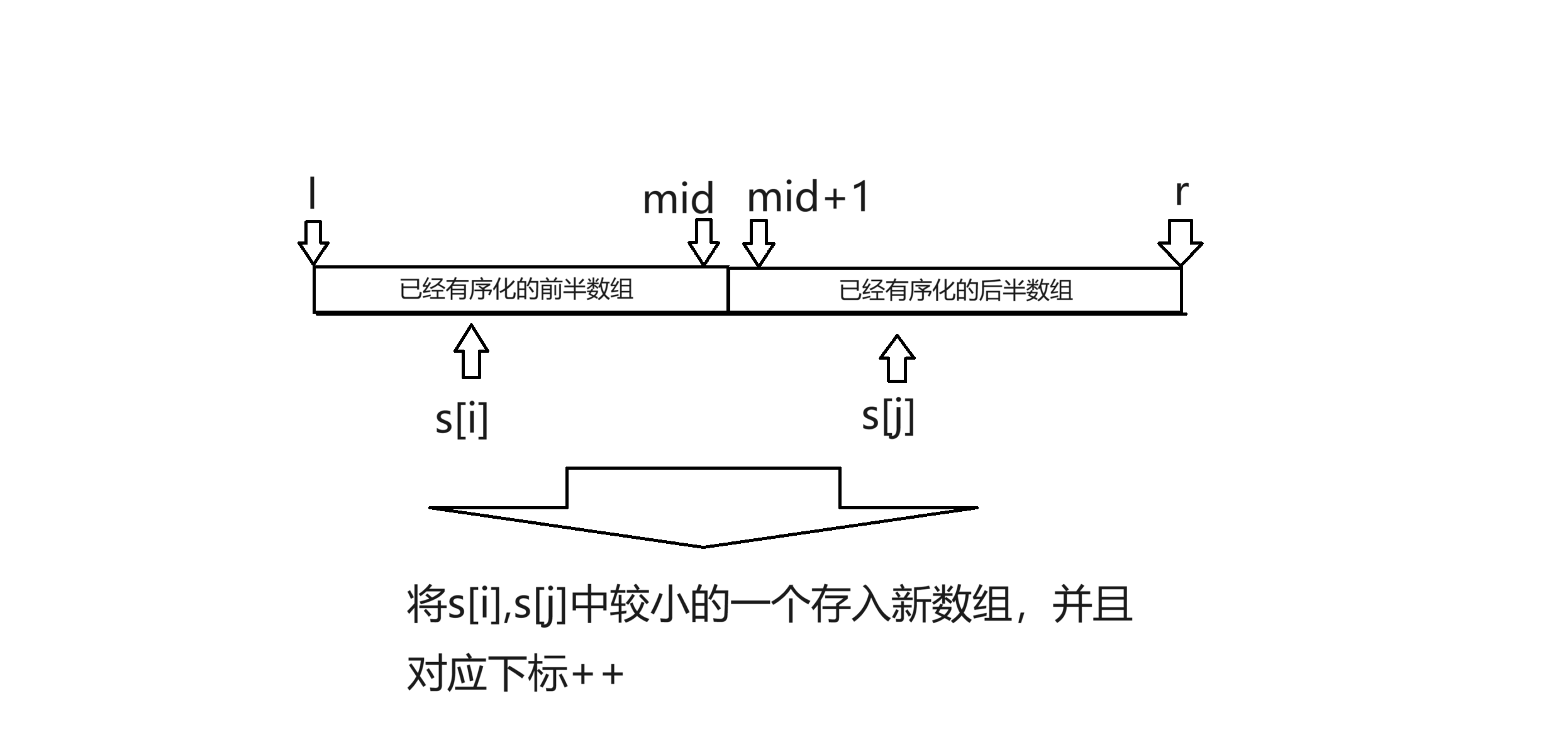
2.
合并两个数组。利用两个指针i,j分别指向两个数组的起始位置，如果s[i]<s[j]就将s[i]放入新数组，反之放入s[j]。
int temp[1000010];//新数组
int k = 0,i = l,j = mid+1;//k负责控制新数组的下标
while(i<=mid&&j<=r)
{
if(s[i]<s[j]) temp[k++] = s[i++];
else temp[k++] = s[j++];
}
3.
因为我们上面使用的循环条件时while(i<=mid&&j<=r)，所以当一个数组中的全部元素全部放入新数组时，另一个数组可能会还有剩余的数据，所以我们需要将这些数据也放入新数组中。
while(i<=mid) temp[k++] = s[i++];
while(j<=r) temp[k++] = s[j++];
4.
最后需要将新数组中的数据储存回原数组中，因为递归的过程中需要再次用到原数组，所以必须储存回去。
for(int i = l,j = 0;i<=r;i++,j++) s[i] = temp[j];//i控制原数组，j控制临时数组
完整代码如下：
int n;
int s[1000010];
void a(int s[], int l, int r)
{
if (l >= r)return;
int temp[1000010];
int mid = l + r >> 1;
a(s, l, mid);
a(s, mid + 1, r);
int k = 0, i = l. j = mid + 1;
while (i <= mid && j <= r)
{
if (s[i] < s[j])temp[k++] = s[i++];
else temp[k++] = s[j++];
}
while (i <= mid) temp[k++] = s[i++];
while (j <= r)temp[k++] = s[j++];
for (int i = l, j = 0; i <= r; i++, j++)
{
s[i] = temp[j];
}
}
法四：选择排序(对应题目6-21 实验7_13_选择排序)
选择排序算法描述如下：
从a[0]到a[n-1]这段元素中找最小元素a[min]，a[0]和a[min]交换；接着，从a[1]到a[n -1]这段元素中找最小元素a[min]，a[1]和a[min]交换；依次类推，直到从a[n－2]到a[n -1]这段元素中找最小元素a[min]，a[n－2]和a[min]交换。
//函数功能：找数组中的最小值元素，并返回其下标
//参数说明：数组名，查找起始位置下标，查找终止位置下标
int findMin(int data[], int startLoc. int endLoc)
{
int minnum = startLoc;//用minnum表示最小值下标
for (int i = startLoc; i <= endLoc; i++)
{
if (data[i] < data[minnum]) minnum = i;//更新最小值
}
return minnum;
}
//输出数组中所有元素
//参数说明：数组，数组中已有元素个数
void outputData(int data[], int elementCount)
{
//注意格式
for (int i = 0; i < elementCount-1; i++)
{
printf("%d ", data[i]);
}
printf("%d\n", data[elementCount - 1]);
}
//选择排序（升序）
//参数说明：数组，数组中已有元素个数
void selectSort(int data[], int elementCount)
{
for (int i = 0; i < elementCount-1; i++)
{
int x = data[i];
//找到从a[i]到a[n -1]这段元素中找最小元素a[min]的下标
int num = findMin(data, i, elementCount - 1);
//交换当前值与最小值
data[i] =data[num];
data[num] = x;
//输出
outputData(data, elementCount);
}
}
法五：选择排序（对应题目6-19 实验7_12_插入排序）
将数组a的前n个元素按照升序的方式排序。
插入排序算法描述如下：
初始序列：49 38 65 97 76 13 27 49
将元素(38) 插入合适位置： [38 49] 65 97 76 13 27 49
将元素(65) 插入合适位置： [38 49 65] 97 76 13 27 49
将元素(97) 插入合适位置： [38 49 65 97] 76 13 27 49
将元素(76) 插入合适位置： [38 49 65 76 97] 13 27 49
将元素(13) 插入合适位置： [13 38 49 65 76 97] 27 49
将元素(27) 插入合适位置： [13 27 38 49 65 76 97] 49
将元素(49) 插入合适位置： [13 27 38 49 49 65 76 97]
void InsertSort(int a[], int n)
{
for (int i = 1; i < n; i++)//第一个数不需要排，从第二个数开始排
{
int temp =a[i];//将需要储存的数储存到temp中
for (int j = i-1; j>=0; j--);//从第i个数之前开始寻找temp所在的位置
{
//如果说a[j]比temp大，那么temp所在的位置一定在a[j]之前，所以我们就将这个数后移一位
//从而在j之前为temp留出一个位置用来储存
if (a[j] > temp) a[j + 1] = a[j];
else//如果a[j]<=temp，那么temp就在a[j]的后一个位置
{
//将a[j+1]这个位置给temp用来储存
a[j + 1] = temp;
break;
}
//特殊判断0，否则就会数组越界
if (j == 0)
{
a[0] = temp;
}
}
for (int j = 0; j < n-1. j++)
{
printf("%d ", a[j]);
}
printf("%d\n", a[n - 1]);
}
}
6-18 实验7_10_发子弹
按照题目模拟就好（看注释）。
注意一个细节，题目中要求调整一直进行，直到子弹数相等为止。
但是当子弹数相等时，继续进行调整并不会改变数组中的子弹数，所以这个结束条件其实不需要考虑，直接进行num次即可，但是这时后复杂度就会提高，可能会超时。
但是这道题的测试数据比较水，并没有专门的考虑这个结束条件，所以直接写就好。
以下是不考虑以上细节的代码：
void distribute(int* bullets, int size, int number)
{
while (number--)//进行num次
{
int temp1 = 0, temp2;.//用两个变量储存移动的子弹数
for (int i = 0; i < size; i++)//遍历一遍数组
{
//首先：如果是奇数，就++
if (bullets[i] % 2 != 0) bullets[i]++;
//将需要转移的子弹数储存到temp2
temp2 = bullets[i] / 2;
//然后储存剩余子弹数
bullets[i] /= 2;
//加上bullets[i-1]转移的子弹数temp1加到buttles[i]
bullets[i] += temp1;
//更新temp1
temp1 = temp2;
}
//最后，将buttles[size-1]转移的子弹数加到bettles[0]
bullets[0] += temp1;
}
}
6-20 实验7_11_循环移位
首先讲比较好想的一种方法
法一：
我构造一个循环是的序列每次推移一位，然后将该循环重复执行num次，就相当于是推移了num位
void shift(int* array, int num, int size)
{
int temp1 = 0, temp2;
while (num--)//循环num次
{
for (int i = size - 1, j = 0; j <= size;. j++)//遍历一遍数组
{
//temp2储存当前的值，准备赋值到前一个位置
temp2 = array[i];
//将array[i+1]的值赋值给当前的array[i]
array[i] = temp1;
//更新temp1
temp1 = temp2;
//指针前移一位
i -= 1;
//如果指针超出边界，就推移到数组最后一位
if (i < 0)
{
i += size;
}
}
//注意j<=size使循环多了一次，使得最后一个数赋值给第一个循环的数。
}
}
法二:
第二种方式，就是直接推移num位。
因为只使用一个数组进行操作，需要考虑的特殊情况很多，所以我们直接使用两个数组
void shift(int* array, int num, int size)
{
int temp[100];//临时数组储存转换后的值
for (int i = 0; i < size; i++)
{
int j = i - num;//j 控制temp数组的小标
if (j < 0)//特殊判断j超边界
{
j += size;
}
//array[i]赋值到新位置temp[j]
temp[j] = array[i];
}
//将临时数组再赋值给原数组
for (int i = 0; i < size; i++)
{
array[i] = temp[i];
}
}
6-22 实验7_14_二分查找
直接讲整数二分，浮点数二分只需要修改细节就好（直接讲两种模版，所有的二分都是这种模版）
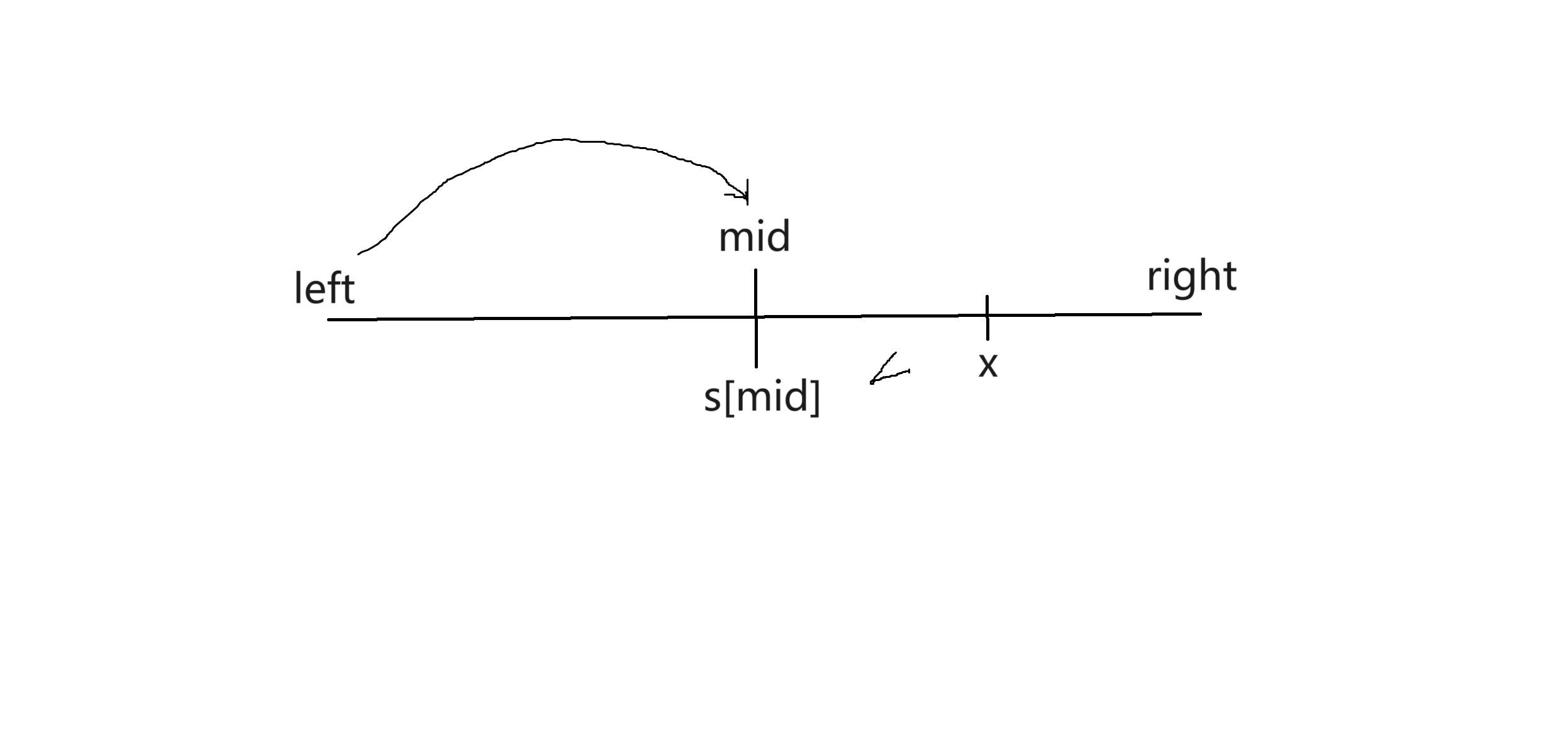
1.
每次找到区间的中点，将s[mid]与x的值相比较。如果是图中的这种情况，x>s[mid] ，所以x存在于右区间。那么调整区间，将区间的左端点调整为mid+1（为什么是mid+1后面会讲），再去循环处理右区间。另一种情况同理。
2.
因为存在边界问题，所以这里的二分需要分情况讨论，对应的代码也有两种。
首先是边界调整的问题。重要的就是那边可以取到最后的值x，就将哪边的边界调整为mid。直接看代码讲。(代码题目是找到x在数组中的位置)
先看第一种：
int l = 0,r = n-1//设置左右端点
while(l<r)
{
int mid = l+r>>1;//设置中点
if(s[mid]>=x) r = mid;
//注意此时x可以在这个判断条件中取到，所以这个条件对应的边界调整为mid
else l = mid+1;
//另一个对应的调整为mid+1或mid-1；
}
第二种：
int l = 0,r = n-1;
while(l<r)
{
int mid = l+r+1>>1;
if(s[mid]<=x) l = mid;
//这时x可以在新的条件中取到，所以对应边界调整为mid,其余同理。
else r = mid-1;
}
3.
另外的，两种情况所移动的方向不同。
当用第一种模版时，将会从数组左向右去找x的值，直到从左向右找到第一个数为止，此时的边界l就是第一个x的位置。
当用第二种模版时，将会从右向左，直到找到一个数为止，l代表找到的第一个x的位置,注意使用这个模版时，mid = l+r+1>>1。
实验7_15_二分查找递归实现
二分递归实现，就是将上述的循环过程改为递归就好.
看代码：
int RecurBinarySearch(int a[], int x, int l, int r)
{
//不进行while循环
if (l >= r)//和while(l<r)的作用是一样的，如果l>=r就结束递归
{
if (a[l] == x) return l;//如果找到就返回下标
else return -1;//找不到就返回-1
}
int mid = l + r >> 1;
if (a[mid] >= x) return RecurBinarySearch(a, x,l, mid);//对右侧进行递归，边界的改变与正常代码相同
else return RecurBinarySearch(a, x,mid + 1, r);//同理
}
之前的博客"acwing week 1 总结" 对二分和排序有详细的讲解，有兴趣看一下。
12次题解周四晚发.
完结撒花！
