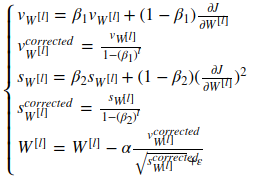2.2 优化算法

 

1. mini-batch梯度下降法

　　size=m：退化为batch，当训练样本过多时，单次迭代需要处理过多的训练样本

　　size=1：随机梯度下降法，产生大量噪声（但通过减小学习率，噪声可以减少），缺点是失去了向量化带来的加速。

 

　　使用mini-size，每次遍历所有样本时，可以进行m/size次梯度下降

　　选取原则：

训练集较小时(<2000)，直接使用batch梯度下降

一般的mini-batch大小为64-512

　（另：选取大小要与CPU/GPU内存相符

2.momentum

2.1 指数加权平均

　　$v_{t}=\beta v_{t-1}+(1-\beta)\theta_{t}$

　　修正偏差：为了解决最开始迭代时，$v_{t}$低于真实值，额外引入一个偏差修正

　　$v_{t}=\frac{\beta v_{t-1}+(1-\beta)\theta_{t}}{1-\beta^{t}}$

2.2 momentun 梯度下降　　　　

 

 

　　如图，为了使得每次梯度下降时的走向不像蓝线那样有很多的纵向分量，而希望走向像红线一样更多的是横向分量，我们引入了momentun梯度下降

　　

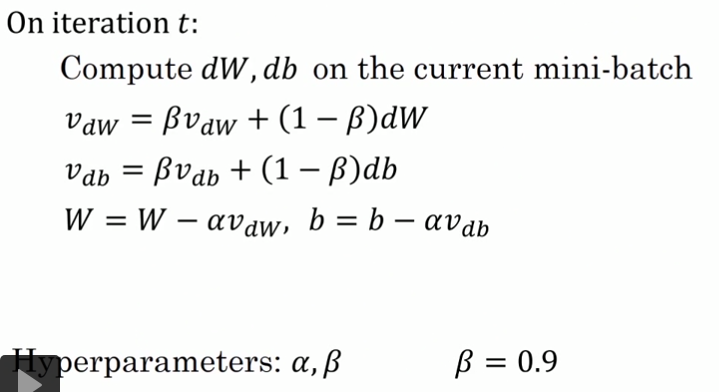
　　作者建议一般将参数$\beta$设为0.9

3. RMSprop

 

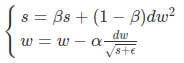
β的典型值是0.999。公式中还有一个ϵ，这是一个很小的数，典型值是10^-8

4.Adam

　　β1=0.9,β2=0.999,ϵ=10^−8。Adam算法相当于先把原始梯度做一个指数加权平均，再做一次归一化处理，然后再更新梯度值。

　　只需调整不用的$\alpha$

 5.作业

　　1.mini-batch

　　Shuffling and Partitioning.建立mini-batch通常需要洗牌和划分两个步骤

　　2. momentum

　　初始化：$v_{dW}^{[l]},v_{db}^{[l]}$

　　迭代：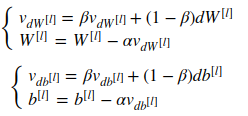

　　3.Adam

　　初始化：$v_{dW}^{[l]},v_{db}^{[l]},s_{dW}^{[l]},s_{db}^{[l]}$

　　迭代：