进位制数及其相互转换
1.进位制数
日常生活中人们都采用十进制数，十进制数用0、1、2、3、4、5、6、7、8、9十个数码表示数值；其基数为10，规则逢十进一，借一当十。
计算机中采用二进制数，二进制数只用两个数码0和1来表示数值；其基数为2，规则逢二进一，借一当二。
由于二进制数书写比较麻烦，因此，计算机中通常又用八进制数或十六进制数来书写和表示信息。
八进制数用0、1、2、3、4、5、6、7八个数码表示数值；其基数为8，规则逢八进一，借一当八。
十六进制数用0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个数码表示数值（在这十六个数码中的A、B、C、D、E、F六个数码，分别代表十进制数中的10、11、12、13、14、15，这是国际上通用的表示法）；其基数为16，规则逢十六进一，借一当十六。
一般来说，若把它们统称为 R进制，则R进位制具有下列特点：
（1）在R进制中，具有R个数字符号，它们是0，l，…，（R- 1）。
（2）在R进制中，由低位向高位是按“逢R进一”的规则进行计数。
（3）R进制的基数是“R”，R进制数的第 i位的权为“Ri ”，约定整数最低位的位序号i为0（i=n，…2，l，0，-l，-2…）。
基数和位权是进位制数的两个要素。所谓某进位制的基数是指该进位制中允许选用的基本数码的个数。不同进位制具有不同的基数，基数表明了某一进位制的基本特征，例如对于二进制，有两个数码（0，1），且由低位向高位是“逢二进一”，故其基数为2。对于某一进位制数，一个数码处在数的不同位置时，它所代表的数值是不同的。例如在十进制数333中，数字3在个位数位置上时表示3，即3×100；数字3在十位数位置上时表示30，即3×101；数字3在百位数位置上时表示300，即3×102。可见每个数码所表示的数值等于该数码乘以一个与数码所在位置有关的常数，这个常数叫位权。位权的大小是以基数为底、数码所在位置的序号为指数的整数次幂。位权表明了同一数字符号处于不同数位时所代表的值不同。
一般而言，对于任意的R进制数
An-1An-2…A1A0 . A-1A-2…A-m (其中n为整数位数，m为小数位数)
可以表示为以下和式：
An-1×Rn-1 +…+A1×R1+A0×R0+A-1×R-1+…A-m×R-m (其中R为基数)
上式称为“按权展开式”。
我们可以用圆括号外的下标值（如：10、2、8、16）表示该括号内的数是哪一个进位制中的数，或在数的最后加上字母D（十进制、D可省略）、B（二进制）、Q（八进制）、H（十六进制）来区分其前面的数是属于哪个进位制。例如，十进制数25可以表示为（25）10或25D或25；二进制数101可以表示为101B或（101）2 。
2．进位制数的相互转换
同一个数值可以用不同的进位制数表示，例如对于十进制数12，可以表示为二进制数1100，可以表示为八进制数14，也可以表示为十六进制数0C。这表明不同进位制只是表示数的不同手段，它们之间必定可以相互转换。下面具体介绍计算机中常用的几种进位制数之间的转换，即十进制与二进制数之间的转换，十进制与八进制或十六进制数之间的转换。
（1）十进制数转换为二进制数
十进制数转换为二进制数的基本方法是：对于整数采用“除2取余”，对于小数采用“乘2取整”。具体做法为：对于十进制数整数，用2连续除要转换的十进制整数及各次所得之商，直除到商等于0时为止，则各次所得之余数即为所求二进制整数由低位到高位的值；对于十进制小数，用2连续乘要转换的十进制小数及各次所得之积的小数部分，直乘到积的小数部分为0（或满足所要求的精度）时为止，则各次所得之积的整数部分即为所求二进制小数由高位到低位的值。当十进制数包含有整数和小数两部分时，可分别将整数和小数转换，然后相加。
例1 将十进制数53.375转换成二进制数。
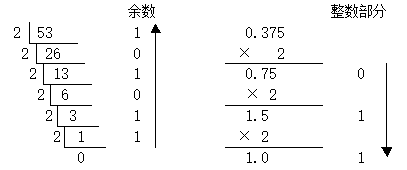
于是， 53.375 = 110101.011B 。
（2）二进制数转换为十进制数
二进制数转换为十进制数的基本方法是将二进制数的各位按权展开相加。
例2 将二进制数11011.101转换成十进制数
11011.101B =1×24+1×23+0×22+1×21+1×20+1×2-1+0×2-2+1×2-3
=16+8+0+2+1+0.5+0+0.125 =27.625
于是， 11011.101B =27.625 。
【例1】逆序的二进制数
问题描述
把一个十进制整数转换成二进制，然后将其二进制倒过来得到的新的数的十进制是多少?
例如，十进制整数6的二进制数为110，逆序后为011，去掉前导0，得到的新数为11，对应的十进制数为3。
输入
输入第1行为一个整数T（1≤T≤100），表示测试用例的组数。
之后T行，每行为1个十进制整数X（0≤X≤231−1）。
输出
二进制数逆序后得到的新的十进制数。
输入样例
3
6
8
1
输出样例
3
1
1
（1）编程思路。
直接采用“除2取余”的方法将输入的十进制整数转换为二进制数保存到a数组中，a[0]保存二进制数的最低位。之后将数组a中保存的二进制数码按权值展开即得到逆序后的十进制数。
（2）源程序。
#include <stdio.h> int main() { int t; scanf("%d",&t); while(t--) { int n; scanf("%d",&n); int a[32]; int len=0; // 保存n对应的二进制的位数 while(n) // 将n转换为二进制数并保存到数组a中 { a[len++] = n%2; n/=2; } int k; for (k=0;k<len && a[k]==0; k++) ; // 去掉前导0 int i,ans = 0; for (i=k;i<len;i++) // 去掉前导0后，a[k]~a[len-1]正好是逆序后的二进制数 { ans=ans*2+a[i]; } printf("%d\n",ans); } return 0; }
将上面的源程序提交给“http://acm.hdu.edu.cn/showproblem.php?pid=5142 NPY and FFT”，可以Accepted。
（3）十进制数转换为R进制数
类似于十进制数转换为二进制数的方法，十进制数转换为R进制数的基本方法是：对于整数采用“除R取余”，对于小数采用“乘R取整”。具体做法为：对于十进制数整数，用R连续除要转换的十进制整数及各次所得之商，直除到商等于0时为止，则各次所得之余数即为所求R进制整数由低位到高位的值；对于十进制小数，用R连续乘要转换的十进制小数及各次所得之积的小数部分，直乘到积的小数部分为0（或满足所要求的精度）时为止，则各次所得之积的整数部分即为所求R进制小数由高位到低位的值。当十进制数包含有整数和小数两部分时，可分别将整数和小数转换，然后相加。
（4）R进制数转换为十进制数
R进制数转换为十进制数的基本方法是将R进制数的各位按权展开，然后进行十进制数相加即可。
【例2】十进制数转换为M进制数
问题描述
将一个十进制数X(1<=X<=10^9)转换成任意进制数M（2<=M<=16）。
输入
一行两个正整数X和M。
输出
输出X的M进制的表示。
输入样例
31 16
输出样例
1F
（1）编程思路1。
直接采用“除M取余”的方法将十进制整数X转换为M进制数。
（2）源程序1。
#include <stdio.h> #include <string.h> char table[16]="0123456789ABCDEF"; int main() { int x,m; scanf("%d%d",&x,&m); char num[33]; int i,j,k=0; do { num[k++]=table[x%m]; x/=m; } while (x!=0); num[k]='\0'; for (i=0,j=k-1;i<j;i++,j--) { char ch; ch=num[i]; num[i]=num[j]; num[j]=ch; } printf("%s\n",num); return 0; }
（3）编程思路2。
由于采用“除M取余”时，所得M进制数是按余数逆序排列的。因此，可以采用递归算法完成转换。
（4）源程序2。
#include <stdio.h> #include <string.h> char table[16]="0123456789ABCDEF"; void change(int n,int m) { if (n==0) return ; change(n/m,m); printf("%c",table[n%m]); } int main() { int x,m; scanf("%d%d",&x,&m); if (x==0) printf("0\n"); else change(x,m); return 0; }
【例3】A+B
问题描述
输入两个不超过8位的十六进制整数，求它们的和并转换为十进制数输出。
注：十六进制数中的10~15分别用大写的英文字母A、B、C、D、E、F表示或小写的英文字母a、b、c、d、e、f表示。
输入
输入包括多组测试用例，每组测试用例占1行，为两个十六进制整数A和B。
输出
对每组测试用例，输出一行。为A+B的十进制数。
输入样例
1 9
A B
a b
输出样例
10
21
21
（1）编程思路。
编写函数int hex2dec(char hex[])将保存在字符串hex中的十六进制整数按权值展开，转换为十进制整数作为函数值返回。
（2）源程序。
#include <stdio.h> #include <string.h> int hex2dec(char hex[]) { int i,num,s=0; for (i=0;hex[i]!='\0';i++) { if (hex[i]>='0' && hex[i]<='9') num=hex[i]-'0'; else if (hex[i]>='A' && hex[i]<='Z') num=hex[i]-'A'+10; else num=hex[i]-'a'+10; s=s*16+num; } return s; } int main() { char a[10],b[10]; while(scanf("%s%s",a,b)!=EOF) { int x; x=hex2dec(a)+hex2dec(b); printf("%d\n",x); } return 0; }
将上面的源程序提交给“http://acm.hdu.edu.cn/showproblem.php?pid=1720 A+B Coming”，可以Accepted。
【例4】可进行数制转换的计算器
问题描述
某计算器能够在不同数制之间进行转换。该计算器显示屏有7位，除了数字0到9之外，它的按钮还包括大写字母A到F，因此它将支持基数2至16的不同进制。
请为该计算器编写不同进制的数的转换程序。
输入
输入包含多组测试用例。每个测试用例占1行，每行将有三个数字。第一个数字是要转换的数。第二个数字是要转换的数的基数。第三个数字是要转换后的数字的基数。
输出
输出将仅是计算器显示屏上显示的转换后的数字。数字应在7位显示屏中右对齐。如果数字太长而无法显示在显示屏上，则在显示屏上右对齐输出“ERROR”（不带引号）。
输入样例
1111000[bk][bk]2[bk]10
1111000[bk][bk]2[bk]16
2102101[bk][bk]3[bk]10
2102101[bk][bk]3[bk]15
[bk][bk]12312[bk][bk]4[bk][bk]2
[bk][bk][bk][bk][bk]1A[bk]15[bk][bk]2
1234567[bk]10[bk]16
[bk][bk][bk]ABCD[bk]16[bk]15
输出样例
[bk][bk][bk][bk]120
[bk][bk][bk][bk][bk]78
[bk][bk][bk]1765
[bk][bk][bk][bk]7CA
[bk][bk]ERROR
[bk][bk]11001
[bk]12D687
[bk][bk][bk]D071
说明：样例中的一个“[bk]”仅表示一个空格，实际的输入和输出时就是一个空格。
（1）编程思路。
为完成基数为A的整数X转换为基数为B的整数Y。可以先采用X按权值展开的方式将X转换为十进制整数Z，再将十进制整数Z按“除B取余”的方法转换为B进制的整数Y。
（2）源程序。
#include <stdio.h> int main() { char str[10]; while (scanf("%s",str)!=EOF) { int a,b; scanf("%d%d",&a,&b); long long sum=0; int i; for (i=0;str[i]!='\0';i++) { if (str[i]>='0'&& str[i]<='9') sum=sum*a+str[i]-'0'; else sum=sum*a+str[i]-'A'+10; } int len=0; int num[30]; do { num[len++]=sum%b; sum/=b; } while(sum); if (len>7) { printf(" ERROR\n"); } else { for (i=0;i<7-len;i++) printf(" "); for (i=len-1;i>=0;i--) if (num[i]>9) printf("%c",num[i]-10+'A'); else printf("%d",num[i]); printf("\n"); } } return 0; }
将上面的源程序提交给“http://acm.hdu.edu.cn/showproblem.php?pid=1335 Basically Speaking”，可以Accepted。
【例5】数位和统计
问题描述
给出2个b进制正整数s和t，算出s和t间所有整数的数位之和。数位和的意思是一个数各个位置上的和。例如，十进制数1357的数位和是16（=1+3+5+7）；十六进制数9A8C的数位和是39（=9+10+8+12）。
输入
第一行一个整数b表示进制，2<=b<=36，A代表10，B代表11，...，Z代表35，以此类推
第二行两个b进制正整数s和t，s、t在10进制下小于1000000。
输出
一个十进制整数表示s和t间所有整数的数位之和
输入样例
11
A 1A
输出样例
76
（1）编程思路。
先将b进制数s和t转换为十进制整数，再用循环对s至t之间所有的整数求每个整数在b进制下的各位数字之和，并将这些求得的和累加起来。
（2）源程序。
#include <stdio.h> int digitSum(int n,int b) // 求10进制整数n对应B进制数的各位数字和 { int s=0; while (n!=0) { s+=n%b; n/=b; } return s; } int change(char s[],int b) // 将b进制数转换为10进制数 { int i,num,sum=0; for (i=0; s[i]!='\0';i++) { num=s[i]-'0'; if (num>9) num-=7; sum=sum*b+num; } return sum; } int main() { int b; scanf("%d",&b); char s[21],t[21]; scanf("%s %s",s,t); int i,x,y; x=change(s,b); y=change(t,b); if (x>y) { int temp; temp=x; x=y; y=temp; } int sum=0; for (i=x; i<=y;i++) sum+=digitSum(i,b); printf("%d\n",sum); return 0; }
【例6】失恋的小W
问题描述
小W在3月7日这天失恋了，伤心的他开始无比讨厌3和7这两个数字，于是他创造了W计数法。W计数法在十进制的基础上去掉了所有含有数字3和数字7的数，例如2的下一个数是4,29的下一个数是40。小W想知道在这种计数法下X到Y之间有多少个数。
输入
一行两个整数表示X、Y，保证1<=X<=Y<=10^9，保证X和Y中不含数字3和数字7。
输出
一行一个整数表示X到Y之间有多少个数。
输入样例
10 100
输出样例
57
（1）编程思路。
所谓的W计数法就是八进制数。在W计数法中，有0,1,2,4,5,6,8,9等八个数码，规则同样“逢八进一”，只不过W计数法中的“8”相当于十进制数中的“6”，W计数法中的“9”相当于十进制数中的“7”。若给出一个十进制数，要转换为W计数法中的数，则十进制的4、5、6应分别转换成3、4、5，8和9要转换为6和7。也就是说，将十进制整数转换成W计数法表示的八进制数时，每位的数字转换为一个数字，若数字超过了7，则减去2；若数字在4~6之间，则减去1；若数字为0~2，则保持不变。W计数法中不存在3和7。
按上面的方法将十进制数X写成W计数法表示的八进制数后，再将这个八进制数转换成十进制数，就知道W计数法中，X是第几个数。同样，将十进制数Y写成W计数法表示的八进制数后，再将这个八进制数转换成十进制数，就知道W计数法中，Y是第几个数。这样就知道X到Y之间有多少个数了。
（2）源程序。
#include <stdio.h> void dec2w(int n,char s[]) // 将10进制整数n转换为w计数法对应的八进制数，并保存到字符串s中 { int i,j,k=0; int a[13]; while (n!=0) { a[k]=n%10; if (a[k]>=7) a[k]=a[k]-2; else if(a[k]>=3) a[k]--; n=n/10; k++; } for (i=k-1,j=0;i>=0;i--,j++) s[j]=a[i]+'0'; s[j]='\0'; } int oct2dec(char s[]) // 将s中保存的8进制数转换为10进制数并返回 { int i,sum=0; for (i=0; s[i]!='\0';i++) { sum=sum*8+s[i]-'0'; } return sum; } int main() { int x,y; scanf("%d %d",&x,&y); char s[13]; dec2w(x,s); x=oct2dec(s); dec2w(y,s); y=oct2dec(s); printf("%d\n",y-x+1); return 0; }
【例7】Base B
问题描述
小红非常喜欢数学。他喜欢研究数字。他知道如何将非负整数表示为基数为P的数字。比如，他知道71的基数为2的数字表示是“1000111”，65的基数为5的数字表示是“230”。但小红希望创建一种所谓“Base B”的数字表达方式。在该表达方式中，其每个数字值不仅等于或大于A，还小于A+B。例如，如果A=1，B=5，那么在“Base 5”中表示数字65，它肯定是“225”，不会是“230”（0超出范围[1,5]）。
225=2*52+2*51+5*50=50+10+5=65
小红对这种表示法非常感兴趣，现在他希望你能为他编写一个程序，帮助他在“Base B”中表示一个数字N。
输入
输入由多组测试用例组成。每组测试用例占1行，每行有三个整数表示N、A、B（0<=N<=10^9、0<=A<=100、2<=B<=100）。
输出
对于每组测试用例，输出N在“Base B”中的表示方式，各数字之间用空格分隔。
输入样例
65 1 5
15 0 2
输出样例
Case 1: 2 2 5
Case 2: 1 1 1 1
（1）编程思路。
先将输入的十进制整数N转换为b进制数。由于“Base B”中要求每位上的数不能小于a。因此，需要进行校正。校正方法为：将转换后得到的b进制数从低位到高位进行处理。如果当前位上数小于a，则从高一位借1，然后当前位加b。
（2）源程序。
#include <stdio.h> int main() { int n,a,b,iCase=0; while (scanf("%d%d%d",&n,&a,&b)!=EOF) { int cnt=0; int digit[32]; while (n) // 将n转换为b进制保存在数组digit中 { digit[cnt++]=n%b; n/=b; } int i; for (i=0;i<cnt-1;i++) // 对小于a的数字进行校正 { while (digit[i]<a) { digit[i]+=b; digit[i+1]--; } } printf("Case %d:",++iCase); for (i=cnt-1;i>=0;i--) { printf(" %d",digit[i]); } printf("\n"); } return 0; }
将上面的源程序提交给http://acm.hdu.edu.cn/showproblem.php?pid=2864 “Base B”，可以Accepted。
【例8】约数的和
问题描述
给定一个十进制整数n，计算n的所有约数在m进制中各位数字的平方和。
例如，给定整数n=10，它的约数有1, 2, 5, 10，表示为2进制数为1, 10, 101, 1010。在2进制中，这些约数的各位数字的平方和为
1^2+ (1^2 + 0^2) + (1^2 + 0^2 + 1^2) + .... = 6 = 110（表示为2进制数）。
输入
输入包括多个测试用例，每个测试用例是一行，包括两个十进制整数n和m（1≤n≤109，2≤m≤16）。
输出
所有约数在m进制中各位数字的平方和。
输入样例
10 2
30 5
输出样例
110
112
（1）编程思路。
先用循环求出n的所有约数并保存到数组a中。再求每个约数在m进制下的各位数字的平方和，并将求得的平方和累加起来。最后将求得的和值（十进制数）转换为m进制数输出。
（2）源程序。
#include <stdio.h> #include <math.h> int main() { int n, m; while (scanf("%d%d",&n,&m)!=EOF) { int i,temp = sqrt(n); int cnt = 0; int a[10005]; for (i = 1;i<=temp;i++) // 求出n的所有因子并保存到数组a中 { if (n%i == 0) { a[cnt++] = i; if (i!= n/i) a[cnt++] = n / i; } } int sum = 0; for (i = 0;i < cnt;i++) // 求出n的所有因子在m进制下的各位数字的平方和 { temp = a[i]; while (temp) { sum += (temp%m)*(temp%m); temp /= m; } } char ans[32]; cnt = 0; while (sum) // 将求得的和值（十进制数）转换为m进制数输出 { temp = sum%m; if (temp < 10) ans[cnt++] = temp + '0'; else ans[cnt++] = temp - 10 + 'A'; sum /= m; } for (i = cnt - 1;i >= 0;i--) printf("%c",ans[i]); printf("\n"); } return 0; }
将上面的源程序提交给 http://acm.hdu.edu.cn/showproblem.php?pid=4432 Sum of divisors，可以Accepted。
