背包问题（1）：基本模型和解法
背包问题的基本模型是：
有一个容量为C的背包，现在要从N件物品中选取若干件装入背包中，每件物品i的重量为W[i]、价值为P[i]。定义一种可行的背包装载为：背包中物品的总重不能超过背包的容量，并且一件物品要么全部选取、要么不选取。定义最佳装载是指所装入的物品价值最高，并且是可行的背包装载。
例如，设C= 12，N=4，W[4]={2，4，6，7}，P[4]={ 6，10，12，13}，则装入W[1]和W[3]，最大价值为23。
若采用贪心法来解决0/1背包问题，可能选择的贪心策略一般有3种。每种贪心策略都是采用多步过程来完成背包的装入，在每一步中，都是利用某种贪心准则来选择将某一件物品装入背包。
（1）选取价值最大者。
贪心策略为：每次从剩余的物品中，选择可以装入背包的价值最大的物品装入背包。这种策略不能保证得到最优解。例如，设C=30，有3个物品A、B、C，W[3]={28，12，12}，P[3]={30，20，20}。根据策略，首先选取物品A，接下来就无法再选取了，此时最大价值为30。但是，选取装B和C，最大价值为40，显然更好。
（2）选取重量最小者。
贪心策略为：从剩下的物品中，选择可以装入背包的重量最小的物品装入背包。其想法是通过多装物品来获得最大价值。这种策略同样不能保证得到最优解。例如，设C=30，有3个物品A、B、C，W[3]={13，14，15}，P[3]={20，30，40}。根据策略，首先选取物品A，接下来选取B，之后就无法再选取了，此时最大价值为50。但是，选取装B和C，最大价值为70，显然更好。
（3）选取单位重量价值最大者
贪心策略为：从剩余物品中，选择可装入背包的P[i]/W[i]值最大的物品装入。这种策略还是不能保证得到最优解。例如，设C=40，有3个物品A、B、C，W[3]={15，20，28}，P[3]={15，20，30}。按照策略，首先选取物品C（p[2]/w[2]>1），接下来就无法再选取了，此时最大价值为30。但是，选取装A和B，最大价值为35，显然更好。
由上面的分析可知，采用贪心法并不一定可以求得最优解。
背包问题用贪心和搜索求解的效果不佳，其标准的解法是动态规划。
1．编程思路1。
按每一件物品装包为一个阶段，共分为n个阶段。
（1）建立递推关系
设f[i][j]为背包容量j，可取物品范围为i、i+1、…、n的最大效益值。例如，f[1][c]的含义是容量为c的背包、可在1~n件物品中选择物品装入背包后所得的最大效益值。
当0≤j<w[i] 时，物品i不可能装入。最大效益值与f[i+1][j] 相同。
当j≥w[i] 时，有两个选择：
1）不装入物品i，这时最大效益值为f[i+1][j] ；
2）装入物品i，这时已产生效益p[i]，背包剩余容量 j−w[i]，可以选择物品i+1、…、n来装，最大效益值为f[i+1][j−w[i]] + p[i]。
期望的最大效益值是两者中的最大者。于是递推关系（或称状态转移方程）如下：
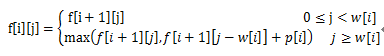
其中w[i]、p[i] 均为正整数，i=1、2、…、n。
边界条件为： f[n][j]=p[n] 当j≥w[n] 时 （最后1件物品可装包） ；
f[n][j]=0 当 j<w[n] 时 （最后1件物品不能装包）。
所求最大效益即最优值为f[1][c]。
（2）逆推计算最优值
for (j=0;j<=c;j++) // 首先计算边界条件f[n][j]
if (j>=w[n])
f[n][j]=p[n];
else
f[n][j]=0;
for(i=n-1;i>=1;i--) // 逆推计算f[i][j] （i从n-1到1）
for(j=0;j<=c;j++)
if (j>=w[i] && f[i+1][j]<f[i+1][j-w[i]]+p[i])
f[i][j]= f[i+1][j-w[i]]+p[i];
else
f[i][j]=f[i+1][j];
printf("最优值为%d\n",f[1][c]);
（3）构造最优解
若f[i][cw] > f[i+1][cw] （ i=1、2、…、n−1， cw的初始值为c）
则x[i]=1； 装载w[i]， cw=cw−x[i]*w[i]。
否则，x[i]=0，不装载w[i]。
最后，所装载的物品效益之和与最优值比较，决定w[n]是否装载。
2．源程序1及运行结果。
#include <stdio.h> #define MAXN 500 #define MAXC 50000 int f[MAXN][MAXC]; int main() { int p[MAXN],w[MAXN]; int n,c; printf("请输入物品的个数 N:"); scanf("%d",&n); printf("请输入背包容量 C："); scanf("%d",&c); printf("请依次输入每种物品的重量："); int i,j; for (i=1;i<=n;i++) scanf("%d",&w[i]); printf("请依次输入每种物品的价值："); for (i=1;i<=n;i++) scanf("%d",&p[i]); for (j=0;j<=c;j++) // 首先计算边界条件f[n][j] if (j>=w[n]) f[n][j]=p[n]; else f[n][j]=0; for (i=n-1;i>=1;i--) // 逆推计算f[i][j] （i从n-1到1） for(j=0;j<=c;j++) if (j>=w[i] && f[i+1][j]<f[i+1][j-w[i]]+p[i]) f[i][j]= f[i+1][j-w[i]]+p[i]; else f[i][j]=f[i+1][j]; int cw=c; printf("背包所装物品如下：\n"); printf(" i w(i) p(i) \n"); printf("----------------------\n"); int sp=0,sw=0; for (i=1;i<=n-1;i++) // 以表格形式输出结果 if (f[i][cw]>f[i+1][cw]) { cw-=w[i]; sw+=w[i]; sp+=p[i]; printf("%3d %8d %8d\n",i,w[i],p[i]); } if (f[1][c]-sp==p[n]) { sw+=w[n];sp+=p[n]; printf("%3d %8d %8d\n",n,w[n],p[n]); } printf("装载物品重量为 %d ,最大总价值为 %d\n",sw,sp); return 0; }
编译并执行以上程序，可得到如下所示的结果。
请输入 n 值:6
请输入背包容量：60
请依次输入每种物品的重量：15 17 20 12 9 14
请依次输入每种物品的价值：32 37 46 26 21 30
背包所装物品如下：
i w(i) p(i)
----------------------
2 17 37
3 20 46
5 9 21
6 14 30
装载物品重量为 60 , 最大总价值为 134
3．编程思路2。
思路1中采用逆推的方法来求解的。实际上在应用动态规划时，还可以顺推求解。
（1）建立递推关系
设f[i][j]为背包容量j，可取物品范围为1、2、…、i的最大效益值。
当0≤j<w[i] 时，物品i不可能装入。最大效益值与f[i−1][j] 相同。
当j≥w[i] 时，有两种选择：
1）不装入物品i，这时最大效益值为f[i−1][j] ；
2）装入物品i，这时已产生效益p[i]，背包剩余容量j−w[i]，可以选择物品1、2、…、i−1来装，最大效益值为f[i−1][j−w[i]]+p[i] 。
期望的最大效益值是两者中的最大者。于是有递推关系
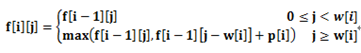
边界条件为： f[1][ j]= p[1] 当 j≥w[1] 时；
f[1][ j] = 0 当j<w[1] 时。
所求最大效益即最优值为f[n][c]。
（2）顺推计算最优值
for(j=0;j<=c;j++) // 首先计算边界条件f[1][j]
if (j>=w[1] ) f[1][j]=p[1];
else f[1][j]=0;
for (i=2;i<=n;i++) // 顺推计算f[i][j] （i从2到n）
for (j=0;j<=c;j++)
if(j>=w[i] && f[i-1][j]<f[i-1][j-w[i]]+p[i])
f[i][j]= f[i-1][j-w[i]]+p[i];
else f[i][j]=f[i-1][j];
printf("最优值为%d\n",f[n][c]);
（3）构造最优解
若f[i][cw] > f[i-1][cw] （ i=1、2、…、n−1， cw的初始值为c）
则x[i]=1； 装载w[i]， cw=cw−x[i]*w[i]。
否则，x[i]=0，不装载w[i]。
最后，所装载的物品效益之和与最优值比较，决定w[1]是否装载。
4．源程序2及运行结果。
#include <stdio.h> #define MAXN 500 #define MAXC 50000 int f[MAXN][MAXC]; int main() { int p[MAXN],w[MAXN]; int n,c; printf("请输入物品的个数 N:"); scanf("%d",&n); printf("请输入背包容量 C："); scanf("%d",&c); printf("请依次输入每种物品的重量："); int i,j; for (i=1;i<=n;i++) scanf("%d",&w[i]); printf("请依次输入每种物品的价值："); for (i=1;i<=n;i++) scanf("%d",&p[i]); for(j=0;j<=c;j++) // 首先计算边界条件f[1][j] if(j>=w[1] ) f[1][j]=p[1]; else f[1][j]=0; for(i=2;i<=n;i++) // 顺推计算f[i][j] （i从2到n） for(j=0;j<=c;j++) if(j>=w[i] && f[i-1][j]<f[i-1][j-w[i]]+p[i]) f[i][j]= f[i-1][j-w[i]]+p[i]; else f[i][j]=f[i-1][j]; int cw=c; printf("背包所装物品如下：\n"); printf(" i w(i) p(i) \n"); printf("----------------------\n"); int sp=0,sw=0; for (i=n;i>=2;i--) // 以表格形式输出结果 if(f[i][cw]>f[i-1][cw]) { cw-=w[i]; sw+=w[i]; sp+=p[i]; printf("%3d %8d %8d\n",i,w[i],p[i]); } if(f[n][c]-sp==p[1]) { sw+=w[1];sp+=p[1]; printf("%3d %8d %8d\n",1,w[1],p[1]); } printf("装载物品重量为 %d ,最大总价值为 %d\n",sw,sp); return 0; }
编译并执行以上程序，得到如下所示的结果。
请输入 n 值:6
请输入背包容量：60
请依次输入每种物品的重量：15 17 20 12 9 14
请依次输入每种物品的价值：32 37 46 26 21 30
背包所装物品如下：
i w(i) p(i)
----------------------
6 14 30
5 9 21
3 20 46
2 17 37
装载物品重量为 60 , 最大总价值为 134
5．编程思路3。
仔细分析编程思路2及其源程序可发现，第 i 件物品的选取决策只与第i-1件有关，与其他无关，即f[i][j]只与f[i-1][j]有关，f[i-2][*]、f[i-3][*]、…这些存储空间的数据是不会再使用的，空间就浪费了。如果采用一维数组，新的状态直接覆盖在旧的上面，迭代使用，就可把空间复杂度从O(N*C)优化为O(C)。
（1）建立递推关系
设f[j]为背包装载的物品容量不超过j时，可获得的最大效益值。
当0≤j<w[i] 时，物品i不可能装入。f[j]的值不改变，无需处理。
当j≥w[i] 时，有两种选择：
1）不装入物品i，这时最大效益值为f[j] ；
2）装入物品i，这时会产生效益p[i]，这实际上是在背包容量为j−w[i]的背包中装入物品i，最大效益值为f[j−w[i]]+p[i] 。
期望的最大效益值是两者中的最大者。于是有递推关系
f[j]=max(f[j],f[j-w[i]]+p[i])
所求最大效益即最优值为f[c]。
（2）逆推计算最优值。
在前面使用二维数组时，为了计算最优值，采用顺推和逆推的方法都可以，因为使用二维数组时，中间的所有状态都保留了下来。
但是，使用一维数组时，究竟是使用顺推还是逆推，就需要看具体的问题了。
由于本题中每个物品要么不装入，要么只能装入1次（每个物品只有1件）。因此，只能采用逆推的方法计算最优值。写成如下的循环。
for (i=1;i<=n;i++) // 对每个物品进行处理
for(j=c;j>=w[i];j--) // 逆推计算f[j]
f[j]=max(f[j], f[j-w[i]]+p[i]);
为什么要逆序枚举计算呢？
如果是正序枚举的话，循环写成
for (i=1;i<=n;i++) // 对每个物品进行处理
for(j=w[i];j<=c;j++) // 正序（顺序）计算f[j]
f[j]=max(f[j], f[j-w[i]]+p[i]);
下面我们用简单的测试数据作为示例进行详细说明。
设背包容量C=8，有两件物品，重量分别为w1=2，w2=3；价值分别为p1=3，p2=4。
初始时，f[0]~f[8]全部为0，背包没有装入任何物品，其装入价值显然为0。
采用正序枚举时，当i=1，处理第1件物品，依次的计算过程如下：
f[2]=max { f[2], f[2-w1]+p1 } =max { 0, 0+3} =3
f[3]=max { f[3], f[3-w1]+p1 } =max { 0, 0+3} =3
f[4]=max { f[4], f[4-w1]+p1 } =max { 0, f[2]+3} = 6 （这里实际就出问题了，因为第1件物品只有1件，在计算f[2]时装入了1次，这里又装入1次，不可能的）
f[5]=max { f[5], f[5-w1]+p1 } =max { 0, f[3]+3} =6 （同上，第1件物品又装入了1次）
f[6]=max { f[6], f[6-w1]+p1 } =max { 0, f[4]+3} =9 （第1件物品装入了3次）
f[7]=max { f[7], f[7-w1]+p1 } =max { 0, f[5]+3} =9 （同上，第1件物品装入了3次）
f[8]=max { f[8], f[8-w1]+p1 } =max { 0, f[6]+3} =12 （第1件物品装入了4次）
当i=2，处理第2件物品，依次的计算过程如下：
f[3]=max { f[3], f[3-w2]+p2 } =max { 3, f[0]+4} =4 （第2件物品装入了1次）
f[4]=max { f[4], f[4-w2]+p2 } =max { 6, f[1]+4} =6 （实际是第1件物品装入2次）
f[5]=max { f[5], f[5-w2]+p2 } =max { 6, f[2]+4} =7 （第1件物品装入1次，第2件物品装入1次）
f[6]=max { f[6], f[6-w2]+p2 } =max { 9, f[3]+4} =9 （实际是第1件物品装入3次）
f[7]=max { f[7], f[7-w2]+p2 } =max { 9, f[4]+4} =10 （实际是第1件物品装入2次，第2件物品装入1次）
f[8]=max { f[8], f[8-w2]+p2 } =max { 12, f[5]+4} =12 （实际是第1件物品装入4次）
循环处理结束后，最优值f[8]=12，这显然是不对的，因为只有2件物品，全部装入背包，最大价值也只有3+4=7。
如果采用逆序枚举，我们再来分析循环的处理过程。
当i=1，处理第1件物品，依次的计算过程如下：
f[8]=max { f[8], f[8-w1]+p1 } =max { 0, f[6]+3} =3 （物品1装入背包，背包容量为8）
f[7]=max { f[7], f[7-w1]+p1 } =max { 0, f[5]+3} =3 （物品1装入背包，背包容量为7）
f[6]=max { f[6], f[6-w1]+p1 } =max { 0, f[4]+3} =3 （物品1装入背包，背包容量为6）
f[5]=max { f[5], f[5-w1]+p1 } =max { 0, f[3]+3} =3 （物品1装入背包，背包容量为5）
f[4]=max { f[4], f[4-w1]+p1 } =max { 0, f[2]+3} =3 （物品1装入背包，背包容量为4）
f[3]=max { f[3], f[3-w1]+p1 } =max { 0, f[1]+3} =3 （物品1装入背包，背包容量为3）
f[2]=max { f[2], f[2-w1]+p1 } =max { 0, f[0]+3} =3 （物品1装入背包，背包容量为2）
也就是，物品1的重量为2，可装入背包容量为2~8的背包中，得到最大价值为3。
当i=2，处理第2件物品，依次的计算过程如下：
f[8]=max { f[8], f[8-w2]+p2 } =max { 3, f[5]+4} =7 （实际是物品1和物品2装入背包）
f[7]=max { f[7], f[7-w2]+p2 } =max { 3, f[4]+4} =7 （实际是物品1和物品2装入背包）
f[6]=max { f[6], f[6-w2]+p2 } =max { 3, f[3]+4} =7 （实际是物品1和物品2装入背包）
f[5]=max { f[5], f[5-w2]+p2 } =max { 3, f[2]+4} =7 （实际是物品1和物品2装入背包）
f[4]=max { f[4], f[4-w2]+p2 } =max { 3, f[1]+4} =4 （实际是物品2装入背包）
f[3]=max { f[3], f[3-w2]+p2 } =max { 3, f[0]+4} =4 （实际是物品2装入背包）
由上面的计算过程知，逆推计算时，每个物品若装入背包，最多装入1次。
由上面的分析大家也可产生一个印象，若每种物品只有1件，1个物品装入背包最多只能装入1次，则采用逆序递推的方法计算最优值，这也是0/1背包的基本模式；若每种物品有无数件，可以不限次数地装入背包中，则采用顺序（正序）递推的方法计算最优值，这也是完全背包的基本模式。对于0/1背包和完全背包，后面会进行更详细地阐述。
（3）构造最优解。
如果要求输出某个最优解，需要记录每个状态的最优值是由状态转移方程的哪一项推出来的。
如果我们知道了当前状态是由哪一个状态推出来的，就能容易的输出某个最优解了。
为此，最简单的方法是定义数组g[n][C]，其中g[i][j]就记录第i件物品在加入背包时，其状态f[j]是由状态转移方程f[j]=max(f[j], f[j-w[i]]+p[i])哪一项推出。若第i件物品加入了背包，即f[j]= f[j-w[i]]+p[i]，置g[i][j]=1；若第i件物品不加入背包，即f[j]=f[j]，置g[i][j]=0。
改写上面的逆推计算最优值循环如下。
for (i=1;i<=n;i++) // 对每个物品进行处理
for(j=c;j>=w[i];j--) // 逆推计算f[j]
{
if (f[j]<f[j-w[i]]+p[i])
{
f[j]=f[j-w[i]]+p[i];
g[i][j]=1; // 选择第i件物品装入
}
else
g[i][j]=0; // 不选择第i件物品装入
}
由此，可用如下循环输出某个最优解。
int T=c;
for (i=n;i>=1;i--)
{
if (g[i][T])
{
printf("used %d",i);
T-=w[i]; //减去物品i的重量
}
}
当然，为了输出某个最优解，我们又定义了一个二维数组，这样我们采用一维数组进行优化的目的并没有达到，还不如直接像编程思路1或编程思路2那样，直接采用二维数组保存各状态，再构造出最优解。
但是，如果只要求得到最优值，而无需输出某个最优解，采用一维数组解决问题还是非常有意义的。
6．源程序3及运行结果。
#include <stdio.h> #define MAXN 500 #define MAXC 50000 int f[MAXC]={0}; int g[MAXN][MAXC]; int main() { int n,c; printf("请输入物品的个数 N:"); scanf("%d",&n); printf("请输入背包容量 C："); scanf("%d",&c); printf("请依次输入每种物品的重量："); int p[MAXN],w[MAXN]; int i,j; for (i=1;i<=n;i++) scanf("%d",&w[i]); printf("请依次输入每种物品的价值："); for (i=1;i<=n;i++) scanf("%d",&p[i]); for (i=1;i<=n;i++) // 对每个物品进行处理 for(j=c;j>=w[i];j--) // 逆推计算f[j] { if (f[j]<f[j-w[i]]+p[i]) { f[j]=f[j-w[i]]+p[i]; g[i][j]=1; // 选择第i件物品装入 } else g[i][j]=0; // 不选择第i件物品装入 } printf("背包所装物品如下：\n"); printf(" i w(i) p(i) \n"); printf("----------------------\n"); int t=c; for (i=n;i>=1;i--) { if (g[i][t]) { printf("%3d %8d %8d\n",i,w[i],p[i]); t-=w[i]; // 减去物品i的重量 } } printf("装载物品重量为 %d ,最大总价值为 %d\n",c-t,f[c]); return 0; }
编译并执行以上程序，得到如下所示的结果。
请输入物品的个数 N:6
请输入背包容量 C：60
请依次输入每种物品的重量：15 17 20 12 9 14
请依次输入每种物品的价值：32 37 46 26 21 30
背包所装物品如下：
i w(i) p(i)
----------------------
6 14 30
5 9 21
3 20 46
2 17 37
装载物品重量为 60 ,最大总价值为 134
