C语言程序设计100例之（60）：集合
例60 集合
问题描述
一个集合S中有N个整数，找出其中值最大的元素D，满足条件A+B+C=D，并且A、B、C、D这四个不同的整数都属于集合S。
输入
输入包括多组测试用例，每组测试用例由一个整数n（1<=n<=1000），表示S中的元素个数，后跟S中的n个元素，每行一个。S的每个元素都是一个介于-536870912和+536870911（含）之间的不同整数。输入的最后一行包含0。
输出
对于每组测试用例，输出一行，为求得的最大值D，或一行包含“no solution”。
输入样例
5
2
3
5
7
12
5
2
16
64
256
1024
0
输出样例
12
no solution
（1）编程思路。
采用枚举法，但不能用4重循环直接枚举，时间复杂度太高。
先将集合S中的n个元素从小到大进行排列。然后最外层循环从大到小枚举元素D的值（即S[n-1]~S[0]，i=n-1~0），第1层内循环中从小到大枚举元素A的值（即S[0]~S[n-1]，j=0~n-1），再在第1层内循环中这样枚举B和C的值：
1）置初始的B为S[j+1]，记下标head=j+1，置初始的C值为S[n-1]，记下标tail=n-1；
2）若head与tail相等，则对B和C的枚举结束，则当前的A值（s[j]）不可能是满足条件的解，进行A的下一个枚举；
3）求A、B、C的和，即sum= s[j]+s[head]+s[tail]；
4）若sum=s[i]，且下标i与j、head、tail均不相同，则找到最大的D，结束枚举过程，输出D的值；
5）若sum>s[i]，则减小C的值，使sum可以减小到与D可能相等，即tail减1，转3）；
6）若sum<s[i]，则增大B的值，使sum可以增大到与D可能相等，即head加1，转3）；
若所有枚举结束，没有求得最大值D，则输出无解信息“no solution”。
（2）源程序。
#include <stdio.h>
int main()
{
int n;
int s[1010];
while(scanf("%d",&n)&& n!=0)
{
int flag=0;
int i,j,t;
for (i=0; i<n; i++)
scanf("%d",&s[i]);
for (i=0;i<n-1;i++)
for (j=0;j<n-1-i;j++)
if (s[j]>s[j+1])
{
t=s[j]; s[j]=s[j+1]; s[j+1]=t;
}
int ans;
for (i=n-1; i>=0 && flag==0; i--)
{
for (j=0; j<n-1 && flag==0; j++)
{
int head=j+1,tail=n-1;
while (head<tail)
{
int sum=s[j]+s[head]+s[tail];
if (sum==s[i])
{
if (i==j||i==head||i==tail) break;
ans=sum;
flag=1;
break;
}
else if (sum>s[i]) tail--;
else head++;
}
}
}
if (flag==1)
printf("%d\n",ans);
else
printf("no solution\n");
}
return 0;
}
习题60
60-1 等差数列
题目描述
小红特别喜欢等差数列。尤其是公差为1且全为正整数的等差数列。
显然，对于每一个数s，都能找到一个对应的公差为1且全为正整数的等差数列各项之和为 s。这时，小红想知道，满足这样条件的等差数列，最小的首项是多少。
由于小红的数学非常差，尤其是因式分解，所以请你告诉她结果。
输入格式
输入仅包含一行一个整数s (1≤s≤1012)。
输出格式
输出两个正整数，分别表示这个等差数列的首项和末项。请注意输出最小的首项。
输入样例
9
输出样例
2 4
（1）编程思路
设等差数列的首项为a1，项数为n，由等差数列求和公式易得：
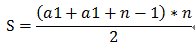
因为a1为正整数，因此2S=(2*a1+n-1)*n >(n-1)*n >(n-1)*(n-1)，所以n-1一定小于sqrt(2*s)，即n一定小于sqrt(2*s)+1。这样可以对项数n从大到小进行枚举，找到第1个满足使a1为正整数的n就可以，因为从大道小进行枚举，所以找到的第1个n值肯定满足使a1最小，a1+n-1就是末项。
（2）源程序。
#include <stdio.h>
#include <math.h>
int main ()
{
long long s;
scanf("%lld",&s);
long long num=2*s;
long long maxx=sqrt(num)+1;
long long i;
long long n;
for (i=maxx;i>=1;i--) // 枚举项数n
{
if ((num-i*i+i)%(2*i)==0 && (num-i*i+i)>0)
{
n=i;
break;
}
}
long long a=(num-n*n+n)/(2*n);
printf("%lld %lld\n",a,a+n-1);
return 0;
}
60-2 临时征用
问题描述
在一条长马路上设置了P（1<=P<=1000）根等距标杆，相邻两根标杆间搭建了一个简易板房，板房编号从1~P-1。N（1<=N<=1000）个工人各自入住某个板房，一个板房中可以入住多名工人。现由于某种需要，需要临时征用一片连续的板房。被征用的板房中若入住有工人，则需要重新安置。
请确定可被征用的连续板房的最大数量，征用后被重新安置的个人不超过C（0<=C<=1000）名。
输入
第1行：三个整数N、P和C。
第2~N+1行：每行包含一个整数X，范围为1~P-1，表示工人入住的板房号。
输出
一个整数，可被征用的连续板房的最大数量。
输入样例
2 6 1
2
3
输出样例
3
（1）编程思路。
定义数组int cnt[1005]={0}，其中cnt[i]表示入住编号为i的板房中工人的人数。
对区间[i,j]进行枚举（1<=i<p，i<=j<p），每次枚举，统计编号在区间[i,j]中板房里入住的人数sum，若sum<=C，则可征用的连续板房数量为j+1-i，记录所有j+1-i中的最大值即可。
（2）源程序。
#include <stdio.h>
int main()
{
int n,p,c;
scanf("%d%d%d",&n,&p,&c);
int cnt[1005]={0},ans=0;
int i,j;
for (i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
cnt[x]++;
}
for (i=1;i<p;i++)
{
int sum=0;
for (j=i; j<p && sum+cnt[j]<=c;j++)
sum+=cnt[j];
if (ans<j-i) ans=j-i;
}
printf("%d",ans);
return 0;
}
60-3 找零钱
问题描述
商店有面值为25分、10分、5分、1分的硬币，给出各硬币的数量和要找给顾客的钱数，问怎么使找给顾客的总的硬币数最少。
输入
输入由一行或多行组成，每行的形式如下：
Q D N P C
式中，Q是25分硬币数，D是10分硬币数，N是五分硬币数，P是1分硬币数，C是要找给客户的钱数（以分为单位）。
输入最后由一行5个零表示结束。
输出
对于每一行输入数据，您的程序应输出：
Dispense # quarters, # dimes, # nickels, and # pennies.
若无法准确找零，则输出 Cannot dispense the desired amount.
输入样例
5 9 9 9 37
0 9 9 9 37
10 10 10 0 37
1 3 0 10 30
1 3 6 10 30
0 0 0 0 0
输出样例
Dispense 1 quarters, 1 dimes, 0 nickels, and 2 pennies.
Dispense 0 quarters, 3 dimes, 1 nickels, and 2 pennies.
Cannot dispense the desired amount.
Dispense 0 quarters, 3 dimes, 0 nickels, and 0 pennies.
Dispense 1 quarters, 0 dimes, 1 nickels, and 0 pennies.
（1）编程思路。
直接用i，j，k三个变量对25分、10分和5分的硬币个数进行穷举。穷举范围为
0≤i≤Q ， 0≤j≤D，0≤k≤N
对穷举的每种情况，计算1分硬币的个数 r=C-( i*25+j*10+k*5)，若0≤r≤P，则当前i,j,k,r值是一种可行的找零方案。方案数cnt++，若找零数量i+j+k+r最小，用数组ans[4]保存这四个值。
（2）源程序1。
#include <stdio.h>
int main()
{
int Q,D,N,P,C;
while(scanf("%d%d%d%d%d",&Q,&D,&N,&P,&C)&&(Q||D||N||P||C))
{
int i,j,k,cnt=0;
int minn=Q+D+N+P+1;
int ans[4]={0};
for (i=0;i<=Q;i++)
for (j=0;j<=D;j++)
for (k=0;k<=N;k++)
{
int r=C-(i*25+j*10+k*5);
if (r>=0 && r<=P)
{
int n=i+j+k+r;
if (n<minn)
{
ans[0]=i; ans[1]=j;
ans[2]=k; ans[3]=r;
cnt++;
minn=n;
}
}
}
if (cnt==0)
printf("Cannot dispense the desired amount.\n");
else
printf("Dispense %d quarters, %d dimes, %d nickels, and %d pennies.\n",ans[0],ans[1],ans[2],ans[3]);
}
return 0;
}
也可以采用深度优先搜索求解，编写如下的源程序2。
（3）源程序2。
#include <stdio.h>
int cnt=0,minn=0;
int c[4]={25,10,5,1};
int w[5],ans[5],num[5];
void dfs(int x,int tot)
{
int i,j,n;
if (x>3) return;
for (i=0; i<=w[x]; i ++)
{
int temp = tot-i*c[x];
if (temp<0) break;
else if (temp==0)
{
cnt++;
for (j=n=0; j<x; j++)
n += num[j];
if (n+i<minn)
{
for (j=0; j<x; j++)
{
ans[j]=num[j];
}
ans[x] = i;
for (j=x+1; j<4; j++)
{
ans[j]=0;
}
minn=n+i;
}
break;
}
else
{
num[x] = i;
dfs(x+1, temp);
}
}
}
int main()
{
int cents;
while(scanf("%d%d%d%d%d",&w[0],&w[1],&w[2],&w[3],¢s)&&(w[0]||w[1]||w[2]||w[3]||cents))
{
minn=w[0]+w[1]+w[2]+w[3]+1;
cnt=0;
dfs(0,cents);
if (cnt==0)
printf("Cannot dispense the desired amount.\n");
else
printf("Dispense %d quarters, %d dimes, %d nickels, and %d pennies.\n",ans[0],ans[1],ans[2],ans[3]);
}
return 0;
}
