C语言程序设计100例之(56):蚂蚁
例56 蚂蚁
问题描述
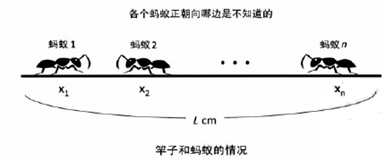
n只蚂蚁以每秒1cm的速度在长为Lcm的竿子上爬行。当蚂蚁爬到竿子的端点时就会掉落。由于竿子太细,两只蚂蚁相遇时,它们不能交错通过,只能各自反向爬回去,蚂蚁反向不需耗时。对于每只蚂蚁,我们知道它距离竿子左端的距离xi,但不知道它当前的朝向。请计算各种情况当中,所有蚂蚁落下竿子所需的最短时间和最长时间。
例如:竿子长10cm,3只蚂蚁位置为2 6 7,最短需要4秒(左、右、右),最长需要8秒(右、右、右)。
输入
第1行:2个整数N和L,N为蚂蚁的数量,L为杆子的长度(1 <= L <= 10^9, 1 <= N <= 50000)
第2 ~ N + 1行:每行一个整数A[i],表示蚂蚁的位置(0 < A[i] < L)
输出
输出2个数,中间用空格分隔,分别表示最短时间和最长时间。
输入样例
3 10
2
6
7
输出样例
4 8
(1)编程思路。
最短时间较容易求。如果每只蚂蚁一开始就向着距离自己最近的竿子那一端爬,即在坐标0~L/2之间的蚂蚁朝着左端爬,L/2~L之间的蚂蚁朝着右端爬,那么蚂蚁之间就不会相遇(因为蚂蚁的速度是一样的)。这样每只蚂蚁的爬行时间对于自己来说都是最小的,又因为是直接朝着自己的方向走的,没有返回也没有相遇,所以在所有蚂蚁都处于自己最短的时间中求出用时最长的那一个时间,就是所有蚂蚁的最短用时。
要使时间最长,蚂蚁一定会相遇,因为只有不断相遇,不断折返,才能增加蚂蚁的爬行时间。在实际计算时,无需根据每只蚂蚁的折返情况来计算时间。
因为可以将所有蚂蚁都视作相同无差别的,那么上图中,若蚂蚁1与蚂蚁2相遇了,我们可以将蚂蚁1变身成蚂蚁2,蚂蚁2变身成蚂蚁1,这样的话,就可以看做蚂蚁其实并没有返回,而是“擦身而过”。这样每只蚂蚁每次遇到别的蚂蚁后就不断变身,那么就相当于每只蚂蚁是独立运动的,并不会影响其运动方向与轨迹。这样,在所有蚂蚁都处于自己最长的时间中求出用时最长的那一个时间,就是所有蚂蚁的最长用时。
(2)源程序。
#include <stdio.h>
int min(int a,int b)
{
return a<b?a:b;
}
int max(int a,int b)
{
return a>b?a:b;
}
int main()
{
int L,n;
int pos;
scanf("%d%d",&n,&L);
int minT=0,maxT=0;
for (int i=1;i<=n;i++)
{
scanf("%d",&pos);
minT=max(minT,min(pos,L+1-pos));
maxT=max(maxT,max(pos,L+1-pos));
}
printf("%d %d\n",minT,maxT);
return 0;
}
习题56
56-1 又是蚂蚁
问题描述
有N只蚂蚁在一根无限长的木棍上,每一只蚂蚁都有一个初始位置和初始朝向(任意两只蚂蚁的初始位置不同)。蚂蚁们以每秒一个单位的速度向前移动,当两只蚂蚁相遇时,它们会掉头(掉头时间忽略不计)。现给出每只蚂蚁的初始位置和初始朝向,请计算出它们在t秒后的位置和朝向。
输入格式
第一行,两个空格隔开的整数n,t(代表蚂蚁数n和时间t,n<=100000,t<=100000);
第2~n+1行每行两个整数,第i+1行代表第i只蚂蚁的初始位置ai(ai的绝对值在1000000以内)及初始朝向bi(bi=1时蚂蚁朝右,bi=-1时蚂蚁朝左)。
输出格式
n行,每行两个整数,第i行代表t秒后第i只蚂蚁的位置及朝向(-1表示朝左,1表示朝右,0表示正在转向中)。
输入样例
4 1
1 1
5 1
3 -1
10 1
输出样例
2 0
6 1
2 0
11 1
(1)编程思路。
按例56的思路,每只蚂蚁每次遇到别的蚂蚁后就不断变身,那么就相当于每只蚂蚁是独立运动的。因此每只蚂蚁只管初始状态和最终状态,只是处理好相遇变身问题即可。
为此定义一个结构体struct Node来表示每只蚂蚁,该结构体包括3个成员,分别表示蚂蚁的位置、方向和编号。
定义两个结构体数组struct Node q[100005],p[100005]; ,其中数组q用来保存初始状态,数组p用来保存最终状态。将初始状态数组按位置从小到大排序后,将每只蚂蚁按位置的相对关系保存到映射数组order中,其中order[i]的值表示排在第i个位置的蚂蚁。
因为不管两只蚂蚁相遇后如何转身,两只蚂蚁的相对位置关系一定不会发生变化。
例如,有A,B两只蚂蚁相遇。相遇前状态为A---> <---B,蚂蚁A向右走,蚂蚁B向左走,相遇转身后的状态为<---A B--->,蚂蚁A向左走,蚂蚁B向右走,即不管A,B两只蚂蚁中间如何相遇转身,两种蚂蚁的相对位置关系一定不变。因此,初始状态下各蚂蚁在按位置从小到大序列中的排名,与在最终状态下按位置从小到大序列中的排名一定一样。这样,N只蚂蚁按例56那样看成每只蚂蚁独立运动可得到N个最终状态,再将最终状态数组按位置从小到大排序,再按映射数组对应的关系,输出各蚂蚁最终的位置和方向即可。在最终状态中,若两只蚂蚁位置相等,注意处理一下其方向即可。
(2)源程序。
#include <stdio.h>
struct Node
{
int s; // 位置
int h; // 方向
int num; // 蚂蚁编号
};
struct Node q[100005],p[100005]; // q用来保存初状态,p用来保存末状态
void mysort(struct Node a[],int n)
{
int i,j;
struct Node t;
for (i=1;i<n;i++)
for (j=1;j<=n-i;j++)
if (a[j].s>a[j+1].s)
{
t=a[j]; a[j]=a[j+1]; a[j+1]=t;
}
}
int order[100005];
int main()
{
int n,t;
scanf("%d%d",&n,&t);
int i;
for (i=1;i<=n;i++)
{
int a,b;
scanf("%d%d",&a,&b);
q[i].s=a;
q[i].h=b;
q[i].num=i;
p[i].s=a+b*t; // t的正负代表了向右还是向左
p[i].num=0; // 对于p数组是用来通过order的映射输出的所以不需要
p[i].h=b;
}
mysort(q,n);
for (i=1;i<=n;i++)
{
order[q[i].num]=i; // 从左到右的蚂蚁编号映射成sort后对应的下标
}
mysort(p,n);
for (i=1;i<=n;i++)
{
if (p[i].s==p[i+1].s) // 正在相遇转向
{
p[i].h=0;
p[i+1].h=0;
}
}
for (i=1;i<=n;i++)
{
int g=order[i];
printf("%d %d\n",p[g].s,p[g].h);
}
return 0;
}
56-2 还是蚂蚁
问题描述
在东西排布的两棵树之间悬挂着一条长为L的细绳,有N只蚂蚁在这条绳上。这些蚂蚁希望通过绳子爬到任何一棵树上,但这条绳太细了,导致两只蚂蚁不能并排爬行,也不能交错而过。
它们想到了一个方法:每只蚂蚁都以每单位时间移动一个单位距离的速度不断向前爬,当迎面碰到另一只蚂蚁时,两只蚂蚁都将立即掉头并继续向前爬。现在,蚂蚁们想知道自己是否能爬下绳子,如果能,它们还希望知道自己爬下绳子所花的时间。为了方便,我们按初始时位置从东到西的顺序对蚂蚁从1开始编号。
输入格式
输入的第一行包含两个正整数 N, L,保证N≤105 ,L≤109,且 N<L。
输入的第二行包含N个正整数,第i 个数pi表示第i只蚂蚁到东侧树木的距离,保证pi随i增大严格递增,且 0<pi <L。
输入的第三行包含N个整数,第i个数di若为1则表示第i只蚂蚁一开始朝向西侧,为0则表示朝向东侧。
输出格式
输出仅一行,包含N个数,第i个数表示第i只蚂蚁爬下绳子所花时间,四舍五入保留到整数。若第i只蚂蚁无法爬下绳子,则输出的第i个数为−1。
输入样例
3 6
1 3 5
1 1 0
输出样例
5 5 3
样例解释
第三只蚂蚁在爬行1 个单位时间后遇见第二只蚂蚁并掉头,再爬行2个单位时间到西侧树木;
第二只蚂蚁在爬行1 个单位时间后遇见第三只蚂蚁并掉头,再爬行1 个单位时间后遇见第一只蚂蚁并掉头,再爬行3 个单位时间到西侧树木;
第一只蚂蚁在爬行2 个单位时间后遇见第二只蚂蚁并掉头,再爬行3 个单位时间到东侧树木。
(1)编程思路。
按例56和习题56-1的思路,可以有如下观点:
1)每只蚂蚁每次遇到别的蚂蚁后就不断变身,那么就相当于每只蚂蚁是独立运动的。
2)不管两只蚂蚁相遇后如何转身,两只蚂蚁的相对位置关系一定不会发生变化。
另外,n只蚂蚁中,设初始时x只蚂蚁向东爬,y只蚂蚁向西爬,任何一次相遇转身后,原来向东爬的蚂蚁向西爬,原来向西爬的蚂蚁向东爬,也就是一次相遇转身不会增加向东爬的蚂蚁只数,也不会增加向西爬的蚂蚁只数。这样,最终状态一定是前x只蚂蚁向东爬,后y只蚂蚁向西爬。前x只向东爬的蚂蚁可以看成是原来向东爬的x只蚂蚁的独立运动(相遇变身)。
这样,问题就简单了,先循环输出向东爬的蚂蚁的爬行距离pi,再循环输出向西爬的蚂蚁的爬行距离L-pi。
(2)源程序。
#include <stdio.h>
int main()
{
int a[100005],st[100005];
int n,l;
scanf("%d%d",&n,&l);
int i;
for (i=1;i<=n;i++)
scanf("%d",&a[i]);
for (i=1;i<=n;i++)
scanf("%d",&st[i]);
for (i=1;i<=n;i++)
{
if (st[i]==0)
{
printf("%d ",a[i]);
}
}
for (i=1;i<=n;i++)
{
if (st[i]==1)
{
printf("%d ",l-a[i]);
}
}
return 0;
}
56-3 直线上行走
问题描述
给定一条直线,长度为L ,用区间表示为[0, L]。在直线上有N个人,每个人有一个初始位置pos(用到直线上端点0的距离表示)和初始方向dir('p' 或 'P' 表示向端点L行走, 'n'或'N'表示向端点0行走),然后所有的人都开始沿着自己的方向用相同的速度v行走,若走到端点0或端点L,则此人掉下去;若两个方向相反的人碰到一起,则分别掉头,继续行走(速度不变)。
求出最后掉下去的人和掉下去的时间。
输入
输入包括多组测试用例,每组测试用例的格式描述如下:
第1行包括一个整数(N<32000)。N=0表示输入的结束。
第2行包含两个浮点数,长度L和速度V。
在接下来的N行中,每行包括三个数据 DIR POS NAME,其中
POS:每个人的初始位置(0<=POS<=L),初始位置已按从小到大排列。
DIR:每个人的初始行走方向,“p”或“P”表示正方向,“n”或“N”表示负方向。
NAME:行走者的姓名(最多250个字符)。
输出
每个测试用例的输出由一行组成。该行第一个值是最后一个掉下去的人的掉下时间,该值输出宽度为13且保留两位小数。第二个值是最后一个掉下去的人的姓名。两者之间使用单个空格字符分隔。
输入样例
1
13.5 2
p 3.5 Smarty
4
10 1
p 1 Helga
n 3 Joanna
p 5 Venus
n 7 Clever
0
输出样例
5.00 Smarty
9.00 Venus
(1)编程思路。
由于相遇只是交换方向,速度不变,因此可以视为两个人只是“擦肩而过”,各自的速度方向均未发生变化,这样转换之后的整体的效果和之前的整体的效果是一样的。那么,求最后掉下的时间就可以直接求每个人走到各自方向的端点所需要的时间,然后求最大值即可。此时,设掉下去时间最大的人为A。
如何求最后掉下去的人是谁呢?最后掉下去的人肯定是和A相遇转身过的人一直不停的相遇转身的最后一个人。即,若A和B相遇,之后B又和C相遇,之后C又和…的最后一个人。
由于N个人的初始位置按从小到大,这样从A开始,沿着A的行走方向的与A的方向相反的第count个人,就是最后和A碰撞之后的人碰撞的那个人,也就是最后掉下去的人。
(2)源程序。
#include <stdio.h>
struct Node
{
int dir;
double pos;
char name[255];
};
struct Node person[32005];
int main()
{
int n;
while (scanf("%d",&n) && n)
{
double l, v;
scanf("%lf%lf",&l,&v);
char dir[3];
int i;
for (i = 0; i<n; i++)
{
scanf("%s %lf %s",dir,&person[i].pos,person[i].name);
person[i].dir = ((dir[0] == 'p' || dir[0] == 'P')? 0 : 1);
}
double max_t = 0;
int max_id;
for (i = 0; i < n; i ++)
{
if (person[i].dir == 1)
{
if (max_t < person[i].pos / v)
{
max_t = person[i].pos / v;
max_id = i;
}
}
else
{
if (max_t < (l - person[i].pos) / v)
{
max_t = (l - person[i].pos) / v;
max_id = i;
}
}
}
int count = 0;
int id = 0;
if (person[max_id].dir == 0)
{
for (i = max_id + 1; i < n; i++)
{
if (person[i].dir == 1)
{
count++;
}
}
id = max_id + count;
}
else
{
for (i = 0; i<max_id; i++)
{
if (person[i].dir == 0)
{
count++;
}
}
id = max_id - count;
}
printf("%13.2f %s\n", (int)(max_t*100)/100.0, person[id].name);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号