C语言程序设计100例之（53）：蚂蚁移动
例53 蚂蚁移动
问题描述
某三角形中各边长为1的小三角形按下图所示的方式用连续整数编号。
一只蚂蚁需要从编号为M的三角形移动到编号为N的三角形。蚂蚁只能通过一个三角形的边移动到另一个三角形，不能通过顶点从一个三角形移动到另一个三角形。蚂蚁通过的边数作为蚂蚁移动路线的长度。
编写程序计算从编号为M的三角形移动到编号为N的三角形的最短移动路线的长度。
输入
输入包含两个整数M和N，范围从1到100000000，用空格分隔。
输出
输出应包含最短路径的长度。
输入样例
6 12
输出样例
3
（1）编程思路。
观察三角形中的编号可知，每行最后一个小三角形的编号是行号的平方值，每行第1个小三角形的编号就是上一行行号的平方值加1。例如，第3行第1小三角形的编号为(3-1)*(3-1)+1=5，最后一个小三角形编号为3*3=9。利用这个规律，可以采用二分法计算出编号为X的小三角形位于图中的第几行第几列。
对于题目给出的两个小三角形M和N，要算出它们之间的行走距离，需要从一个地方按行走、按左下方向走和按右下方向走，把这三个距离都加起来就得到了行走距离。
以样例为例进行说明。编号为M=6的三角形位于第3行，记为mr=3，距离其左端mb=6-5=1，距离其右端me=9-6=3；编号为N=12的三角形位于第4行，记为nr=4，距离其左端nb=12-10=2，距离其右端ne=16-12=4。将|nr-mr|、|nb/2-mb/2|和|nb/2-mb/2|三个绝对值加起来就是最短的行走距离。
|nr-mr|+|nb/2-mb/2|+|nb/2-mb/2|=|4-3|+|2/2-1/2|+|4/2-3/2|=1+1+1=3。
（2）源程序。
#include <stdio.h>
int abs(int x)
{
return x>0?x:-x;
}
int find(int x)
{
int left=0,right=32000,mid;
int row,col;
while (left<=right)
{
mid=(left+right)/2;
if (mid*mid<x)
{
row=mid;
left=mid+1;
}
else
{
right=mid-1;
}
}
return row+1;
}
int main()
{
int m, n, ans;
while(scanf("%d%d", &m, &n)==2)
{
int mline = find(m);
int nline = find(n);
int mbegin=(mline-1)*(mline-1)+1;
int nbegin=(nline-1)*(nline-1)+1;
int mend=mline*mline;
int nend=nline*nline;
ans = abs(nline - mline) +abs((n-nbegin)/2-(m-mbegin)/2)+
abs((nend-n)/2-(mend-m)/2);
printf("%d\n", ans);
}
return 0;
}
习题53
53-1 巢房的坐标
问题描述
蜜蜂生活在一个蜂巢里。一个蜂巢由许多六角形的小巢房组成。为描述这些巢房的位置，可以采用两种方式。一种采用二维坐标系统，每个蜂房用2个整数表示，最中部的用（0,0）表示；另一种采用从蜂房中部的以数字1开始顺时针方向编号来表示，如下图所示。
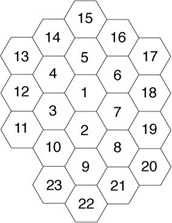
坐标表示法 编号表示法
编写程序，实现从编号表示法到坐标表示法的转换。
输入
输入包含一个或多个表示蜂房编号的整数。每个整数单独排成一行。
输出
输出每个编号表示的蜂房的坐标表示。
输入样例
1
2
3
4
5
输出样例
0 0
0 1
-1 1
-1 0
0 -1
（1）编程思路。
首先，设由1到2的方向记为2，1到3的方向记为3……1到7的方向记为7，它们分别是：(0,1)，(-1,1)，(-1,0)，(0,-1)，(1,-1)，(1,0)；这些规律不仅对于1的周围六个方向有效，对于所有的点都是有效的。
然后记1所在为圈0，2~7为圈1，8~19为圈2，…，以此类推。可以得到第n圈有蜂窝6n个(n>0)。
对于这个等差数列求和，Sum[1~n]=3n^2+3n，包括第0圈的1，则Sum[0..n]=3n^2+3n+1。
读入数字x，解方程3n^2+3n+1=x， 解出来n=[sqrt(12x-3)-3]/6。
如果n为整数，则圈数p=n，否则p=(int)(n)+1。
又可以通过公式 t=x-3*sqr(p)+3*p-1 求出t（x是第n圈的第t个蜂巢）。
可以发现，从上一圈的最后一点，即(p-1，0)走到目的点，首先应在2方向上走1步，再沿(-1，1)走p-1步，其余的5个方向都走p步，此外每走一次，t就要减去相应的值，当t=0时，就可以退出循环，这样就可以得到答案。
（2）源程序。
#include<stdio.h>
#include<math.h>
int main()
{
double x;
int n,t,p,x0,y0,i;
while (scanf("%d",&n)!=EOF)
{
x=(sqrt(12.0*n-3)-3)/6;
p=(int)x;
if (3*p*p+3*p+1!=n)
{
t=n-(3*p*p+3*p+1);
p++;
x0=p-1;
y0=0;
while(t)
{
t--;
y0++; // 先向方向2走一步
for(i=1;i<=p-1 && t;i++,t--) x0--,y0++; // 再向方向3走p-1步
for(i=1;i<=p && t;i++,t--) x0--; // 其他剩余的五个方向各走p步
for(i=1;i<=p && t;i++,t--) y0--;
for(i=1;i<=p && t;i++,t--) x0++,y0--;
for(i=1;i<=p && t;i++,t--) x0++;
for(i=1;i<=p && t;i++,t--) y0++;
}
printf("%d %d\n",x0,y0);
}
else
printf("%d 0\n",p);
}
return 0;
}
53-2 巢房之间的距离
问题描述
蜜蜂生活在一个蜂巢里。一个蜂巢由许多六角形的小巢房组成。我们将任意一个小巢房标记为数字1，然后以顺时针方向标记剩余小巢房来标记这些巢房，如下图所示。
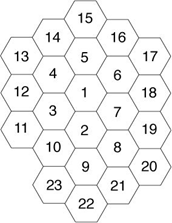
例如，15号和19号巢房相隔4个巢房。连接两个巢房的最短路径之一是通过15-5-6-7-19，因此，一只蜜蜂要在这两个巢房间移动，必须移动4次到相邻巢房才能从15到19。
编写一个程序来计算任意一对巢房之间的距离，定义为最短路径中的巢房数。
输入
输入由几行组成，每行包含两个整数a和b（a，b<=10000），表示巢房编号。除最后一行a=b=0外，整数始终为正。最后一行终止输入，不应进行处理。
输出
对于输入的每对数字（a、b），输出编号为a和b的巢房之间的距离，该距离是从a到b的最小移动次数。
输入样例
19 30
0 0
输出样例
The distance between cells 19 and 30 is 5.
（1）编程思路。
要求蜜蜂在蜂巢中从一个巢房走到另一个巢房最少的移动次数。先按上面习题53-1中的方法，将代表位置的编号数字转换为坐标。然后求得两个坐标之差x，y。如果x，y同号，则相加，否则取x和y绝对值最大的即可。
（2）源程序。
#include<stdio.h>
#include<math.h>
struct Point
{
int x,y;
};
Point change(int n)
{
double x;
Point pos;
int t,p,x0,y0,i;
x=(sqrt(12.0*n-3)-3)/6;
p=(int)x;
if (3*p*p+3*p+1!=n)
{
t=n-(3*p*p+3*p+1);
p++;
x0=p-1;
y0=0;
while(t)
{
t--;
y0++; // 先向方向2走一步
for(i=1;i<=p-1 && t;i++,t--) x0--,y0++; // 再向方向3走p-1步
for(i=1;i<=p && t;i++,t--) x0--; // 向其他剩余的五个方向各走p步
for(i=1;i<=p && t;i++,t--) y0--;
for(i=1;i<=p && t;i++,t--) x0++,y0--;
for(i=1;i<=p && t;i++,t--) x0++;
for(i=1;i<=p && t;i++,t--) y0++;
}
pos.x=x0;
pos.y=y0;
}
else
{
pos.x=p;
pos.y=0;
}
return pos;
}
int main()
{
int n,m,x,y,ans;
Point p1,p2;
while (scanf("%d%d",&n,&m) && n!=0 && m!=0)
{
p1=change(n);
p2=change(m);
x=p1.x-p2.x;
y=p1.y-p2.y;
if ((x<0 && y<0)||(x>0 && y>0))
ans=abs(x+y);
else
ans=abs(x)>abs(y)?abs(x):abs(y);
printf("The distance between cells %d and %d is %d.\n",n,m,ans);
}
return 0;
}
53-3 士兵排队
问题描述
有N个士兵随机分布在操场上，每个士兵的位置由一对（x，y）整数坐标给出。现在要求N个士兵站在同一个水平线，即所有士兵的y坐标相同并且x坐标相邻。移动结束后，整数x和y以及士兵沿水平线的最终顺序可以是任意的。但两名或两名以上士兵最终不得同时占据同一位置。
每个士兵在每次移动过程中，可以向上、向下、向左或向右移动一个单位（即每次移动可以将其x或y坐标加1或减1）。求出所有士兵总的最少移动步数。
输入
输入的第一行包含整数N（1<=N<=10000），表示士兵人数。
以下N行输入为士兵的初始位置，每行包含一对整数x[i]和y[i]（-10000<=x[i]，y[i]<=10000），由单个空白字符分隔，表示第i个士兵的坐标。
输出
输出为最小的移动总数。
输入样例
5
1 2
2 2
1 3
3 -2
3 3
输出样例
8
（1）编程思路。
士兵移动既涉及X分析的移动，也涉及到Y方向的移动，将它们分开讨论。
1）Y方向移动。
要使所有士兵最后位于同一水平线，则最终所有士兵的y坐标相同。
将所有坐标的y值从小到大排序，将y值的中位数midY（midY=y[n/2]）作为最终的Y坐标，可使Y方向的移动步数最少。
Y方向的最小移动步数 stepsY=|y[0]-midY|+|y[1]-midY|+…+|y[n-1]-midY|。
2）X方向移动。
先对所有坐标的x值从小到大排序，由于要移动步数最少，所以最终的x坐标相对位置与排序后的x坐标相对位置相同。
设最终的x坐标起始位置为a，则
x[0] 移动到 a
x[1] 移动到 a+1， 也可以看成将 x[1]-1 移动到 a
……
x[n-1] 移动到 a+n-1 ，也可以看成将 x[n-1]-(n-1) 移动到 a
即将所有x[i]-i移动到相同位置a，由此问题转换为和y方向上相同。重新计算x[i]=x[i]-i，再进行从小到大排序。将新的x[i]值的中位数midX（midX=X[n/2]）作为最终的a坐标，可使X方向的移动步数最少。
X方向的最小移动步数 stepsX=|x[0]-midX|+|x[1]-midX|+…+|x[n-1]-midX|。
总的最小移动步数 steps=stepsX+stepsY。
（2）源程序。
#include <stdio.h>
#include <algorithm>
using namespace std;
int main()
{
int x[10001], y[10001];
int n;
scanf("%d", &n);
int i;
for (i=0;i<n;i++)
scanf("%d%d", &x[i],&y[i]);
sort(x,x+n);
sort(y,y+n);
for (i=0; i<n; i++)
x[i] -= i;
sort(x,x+n);
int midX=x[n/2];
int midY=y[n/2];
int ans=0;
for (i=0; i<n; i++)
ans += abs(x[i]-midX) + abs(y[i]-midY);
printf("%d\n", ans);
return 0;
}
