C语言程序设计100例之（50）：向下的路径

例50  向下的路径

问题描述

有一个size=N的图，如图1所示。然后我们将找到一条从顶部节点到底部节点的向下路径。

 

 

 

 

 

 

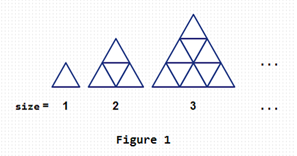
首先，我们选择顶部节点作为开始。然后在任何节点，我们都可以沿着蓝色边缘水平或向下移动，到达下一个节点。当我们到达其中一个底部节点时，移动结束。然后，我们可以得到从顶部节点到底部节点的向下路径。请注意，在移动过程中，每条蓝边最多走过1次。

例如，size=2时，图2中的黄色路径显示了8条向下的路径。

 

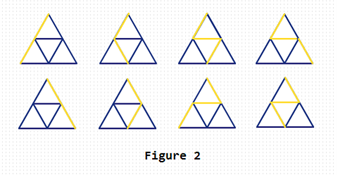
 您的任务是计算存在多少向下的路径。

输入

第一行中有一个整数T（1<=T<=1000），表示总共有T个测试用例。

对于每个测试用例，只有一个整数N（1<=N<=10^18）表示图形的大小。

输出

对于每个测试用例，在一行中输出上述任务的正确答案。

因为答案可能非常大，只输出它除以1000003的余数即可。

输入样例

2

1

2

输出样例

2

8

         （1）编程思路。

        设a[i]表示size=i时从顶部节点到底部节点的向下路径的条数。

        a[1]=2=1+1

        a[2]=8=2*2*a[1]

        a[3]=48=3*2*a[2]=3*2*8 （size=3时，可以先从顶部节点移动到最底行的上一行，此时方法数为a[2]，其结束点一定在上一行的3个节点之一，这3个节点，每个结点均有两种方法向下移动到底行，故a[3]=3*2*a[2]）

        ......

        a[n]= 2*n*a[n-1]

        即：a[n]=2^n*n！

        因为a[n]=2^n*n!，所以当n>1000003时，n！中有1000003这个因数，故ans=0。

（2）源程序。

#include <stdio.h>

#define MAXN 1000003

long long a[MAXN];

int main()

{

    a[0]=0;  a[1]=2;

    int i;

    for (i=2;i<MAXN;i++){

        a[i]=(a[i-1]*2*i)%MAXN;

    }

    int t;

    scanf("%d",&t);

    while(t--){

           long long n;

           scanf("%lld",&n);

              if (n<=MAXN) printf("%lld\n",a[n%MAXN]);

              else printf("0\n");

       }

    return 0;

}

习题50

50-1  三角形计数

        本题选自洛谷题库 （https://www.luogu.org/problem/P2807）

题目描述

把大三角形的每条边n等分，将对应的等分点连接起来（连接线分别平行于三条边），这样一共会有多少三角形呢？编程来解决这个问题。

输入格式

第一行为整数t(≤100)，表示测试数据组数；接下来t行，每行一个正整数n(≤500)。

输出格式

对于每个n，输出一个正整数，表示三角形个数。

输入样例

3

1

2

3

输出样例

1

5

13

        （1）编程思路。

        设a[i]表示边长为i的三角形个数。

        先用下图所示的边长为4的三角形来列举边长n<=4的三角形个数。

 

 

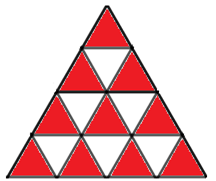
         显然，a[1]=1。

        当i=2时，对应图中上两行。边长为1的小三角形有4个，其中3个顶点向上（红色三角形），1个顶点向下（白色三角形）；边长为2的三角形有1个。所以，a[2]=5。

        当i=3时，对应图中上三行。可以看成是在上两行（i=2）的基础上增加第3行扩展而来。此时，增加了边长为1的小三角形有5个，其中3个顶点向上（红色三角形），2个顶点向下（白色三角形）；增加了边长为2的三角形有2个，顶点均向上；增加了边长为3的三角形1个，顶点向上。所以，a[3]=a[2]+5+2+1=13。

        当i=4时，对应图中全部四行。可以看成是在上面三行（i=3）的基础上增加第4行扩展而来。此时，增加了边长为1的小三角形有7个，其中4个顶点向上（红色三角形），3个顶点向下（白色三角形）；增加了边长为2的三角形有4个，其中3个顶点向上，1个顶点向下；增加了边长为3的三角形2个，顶点均向上；增加了边长为4的三角形1个，顶点向上。所以，a[4]=a[3]+7+4+2+1=27。

        更一般地，i=n时，可以看成是在上n-1行（i=n-1）的基础上增加第n行而来。此时，可分两种情况讨论：

        1）增加的顶点向上的三角形中，边长为1的，增加了n个，边长为2的，增加了n-1个，…，边长为n-1的，增加了2个，边长为n的，增加了1个。共增加了n+(n-1)+…+2+1=(n+1)*n/2个。

        2）增加的顶点向下的三角形中，又按n的奇偶不同分开讨论。当n为偶数时，边长为1的，增加了n-1个，边长为2的，增加了n-3个，…，边长为n/2-1的，增加了2个，边长为n/2的，增加了1个，共增加了(n-1+1)*(n/2) / 2=n*n/4个；当n为奇数时，边长为1的，增加了n-1个，边长为2的，增加了n-3个，…，边长为(n-1)/2的，增加了2个，边长为(n+1)/2的，增加了0个，共增加了((n-1+2)*(n-1)/2) / 2=(n+1)*(n-1)/4个。

        由此得到，若n为偶数，a[n]=a[n-1]+(n+1) * n / 2 + n * n /4

                         若n为奇数，a[n]=a[n-1] + (n + 1 ) * n / 2 + (n+1) * (n-1) / 4

        （2）源程序。

#include <stdio.h>

int main()

{

    int a[501]={0,1};

    int i;

    for (i=2;i<=500;i++)

       {

              if(i%2==0) a[i]=a[i-1]+(1+i)*i/2+i*i/4;

              else a[i]=a[i-1]+(1+i)*(i-1)/4+(1+i)*i/2;

       }

    int t,n;

    scanf("%d",&t);

    for (i = 1;i <= t;i++)

    {

        scanf("%d",&n);

        printf("%d\n",a[n]);

    }

       return 0;

}

50-2  1和1不相邻

问题描述

给定一个正整数n，请求出n位二进制数中，确定不包含相邻1的n位序列的个数。例如，对于n=3，答案为5（序列000、001、010、100、101符合要求，而011、110、111不符合要求）。

输入

第1行给出测试用例的数量T。

对于每个测试用例，在一行中给出一个小于45的正整数n。

输出

每个测试用例的输出都以一行开头，其中包含“Scenario #i:”，其中i是从1开始的用例编号。然后打印一行，其中包含没有相邻1的n位序列数。

输入样例

2

3

1

输出样例

Scenario #1:

5

 

Scenario #2:

2

         （1）编程思路。

         设a[i]表示不包含相邻1的i位二进制数序列的个数。由于1不能连续，那么长度为n的二进制数，第1位是1，则第2位只能为0，情况总数等于a[n-2]，第1位是0，则情况总数等于a[n-1]，因此，a[n]=a[n-1]+a[n-2]。

        （2）源程序。

#include <stdio.h>

int main()

{

    long long a[50];

       a[1] = 2;

       a[2] = 3;

    int i;

       for (i=3; i<=45; i++)

    {

              a[i]=a[i-1]+a[i-2];

       }

       int t,n;

       scanf("%d",&t);

       for (i=1;i<=t;i++)

       {

              scanf("%d",&n);

              printf("Scenario #%d:\n",i);

              printf("%lld\n\n",a[n]);

       }

    return 0;

}

50-3  跳马

问题描述

马在一个n行m列棋盘的左下角（1,1）的位置，它想要走到终点右上角（n，m）的位置。而众所周知，马是要走日子格的。但现在这匹马不想走回头路——也就是说，它只会朝向上的方向跳，不会朝向下的方向跳。

这匹马想从起点跳到终点，一共有多少种走法呢？

输入格式

第一行两个数n，m（n<=100,m<=100），表示一个n行m列的棋盘，马最初是在左下角（1,1）的位置，终点在右上角（n，m）的位置。

输出格式

输出有一行，一个数表示走法数。由于答案可能很大，所以输出答案除以1000000007所得的余数即可。

输入样例

4 4

输出样例

2

        （1）编程思路。

        设F[i] [j] 表示马从左下角（1,1）跳到（i，j）的走法种数。

        由于只能往上跳，即跳动过程中，行i只能增大，因此第1行中的各位置是怎么也跳不上去，即F[1][j]=0（1<=j<=m）。又因为刚开始就在（1,1）这个位置上，从（1,1）往上只能跳两个点（2,3）和（3,2），即F[2][3]=F[3][2]=1。.

        由于位置（i，j），只能从（i-1，j-2），（i-2，j-1），（i-2，j+1），（i-1，j+2）这四个点跳过来，因此有

             F[i][j]= F[i-1][j-2]+F[i-2][j-1]+F[i-2][j+1]+F[i-1][j+2]

        需要注意的是，由于棋盘是有边界的，因此在计算时，对每个点判断一下，如果满足条件就加上，否则不加。例如，若i-1>1 && j-2>=1，F[i-1][j-2]就可以加上；若i-1>1 && j+2<=m，F[i-1][j+2]就可以加上。

        （2）源程序。

#include <stdio.h>

int main()

{

    int f[105][105]={0};

    int n,m;

    scanf("%d%d",&n,&m);

       f[2][3]=f[3][2]=1;

       int i,j;

       for (i=1; i<=n; i++)

    {

              for (j=1; j<=m; j++)

              {

                     if (i==1) f[i][j] = 0;

                     if (i-2>1 && j+1<=m)

                         f[i][j] = (f[i][j]+f[i-2][j+1])%1000000007;

                     if (i-1>1 && j+2<=m)

                         f[i][j] = (f[i][j]+f[i-1][j+2])%1000000007;

                     if (i-1>1 && j-2>=1)

                         f[i][j] = (f[i][j]+f[i-1][j-2])%1000000007;

                     if (i-2>1 && j-1>=1)

                         f[i][j] = (f[i][j]+f[i-2][j-1])%1000000007;

              }

       }

       printf("%d\n",f[n][m]);

       return 0;

}