C语言程序设计100例之（26）：二进制数中1的个数
例26 二进制数中1的个数
问题描述
如果一个正整数m表示成二进制，它的位数为n（不包含前导0），称它为一个n位二进制数。所有的n位二进制数中，1的总个数是多少呢？
例如，3位二进制数总共有4个，分别是4（100）、5（101）、6（110）、7（111），它们中1的个数一共是1＋2＋2＋3=8，所以所有3位二进制数中，1的总个数为8。
输入格式
一个整数T，表示输入数据的组数，接下来有T行，每行包含一个正整数 n（1<=n<=20）。
输出格式
对于每个n ，在一行内输出n位二进制数中1的总个数。
输入样例
3
1
2
3
输出样例
1
3
8
（1）编程思路1。
对于输入的n，n位二进制数m是位数为n并且首位为1的二进制数，且满足：
2n-1 ≤ n位二进制数m < 2n
因为首位为1，n位二进制数的个数就是n-1位的0和1的组合数，即2n-1个。
第1位必须为1，所以第1位的1的个数为2n-1个。
其他n-1位，总位数为(n-1)* 2n-1。其中0和1的个数是一半对一半，所以1的个数为(n-1)* 2n-1/2。
合计1的位数为：2n-1 +(n-1)* 2n-1/2。
因此，n位二进制数中1的个数直接用上式计算出来。计算时，用移位运算来计算2的n次方是一种快速的计算方法。
即n位二进制数中1的个数为 ：1<<(n-1)+(n-1)*(1<<(n-2))。
（2）源程序1。
#include <stdio.h>
int main()
{
int t,n;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
int ans=(1<<(n-1))+(n-1)*(1<<(n-2));
printf("%d\n",ans);
}
return 0;
}
（3）编程思路2。
设数组元素f[i]的值表示i位二进制数中1的个数。因为i位二进制数可以看成是i-1位二进制数的每个数在其最右边分别加上1或0得到的。因此，i位二进制数中1的个数一定是i-1位二进制数中1的个数的二倍，再加上i-1位二进制数的个数（因为每个数最右边如果加上1，1的个数会增加1个，加上0不会增加）。
即 f[i]=2*f[i-1]+2i-2
初始时，f[1]=1， f[2]=2*f[1]+2^0=3 。
（4）源程序2。
#include <stdio.h>
int main()
{
int f[21]={0,1};
for(int i=2;i<=20;i++)
{
f[i]=2*f[i-1]+(1<<(i-2));
}
int t,n;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
printf("%d\n",f[n]);
}
return 0;
}
习题26
26-1 1的个数相同
问题描述
给定一个大于0的整数n，把它转换为二进制，则其二进制数中至少有1位是“1”。编写一个程序，找出比给定的整数n大的最小整数m。要求m和n两个整数转换成二进制数后，二进制数中包含的1的个数相同。
例如，120的二进制数为01111000，则比120大且二进制数中1的个数相同的最小整数为135（10000111）。
输入格式
输入包含若干组数据。每组数据是一个整数 N （1<=N <=65535）。N = 0 时输入结束。
输出格式
对于每组数据，在单独的一行输出一个整数m。
样例输入
92
120
0
样例输出
99
135
（1）编程思路1。
寻找比n大的最小的整数m，最容易想到的方法是从n+1开始穷举。首先把十进制整数n转化为二进制，然后穷举比这个十进制整数大的数m，判断m和n两个数对应的二进制数中1的个数是否相同。判断的方法就是，把十进制数用n&1的位运算依次取出末位然后全部加起来，若两个数的所有二进制位加起来相等，则这两个数的二进制位一定有相同个1。
（2）源程序1。
#include <stdio.h>
int main()
{
int n,a,b,d,m;
while (scanf("%d",&n) && n!=0)
{
a=n; b=0;
while(a)
{
b+=a&1; a>>=1;
}
m=n;
do {
d=0; m++; a=m;
while(a)
{
d+=a&1; a>>=1;
}
} while(d!=b);
printf("%d\n",m);
}
return 0;
}
（3）编程思路2。
对十进制数n转化成的二进制数直接进行位变换，求出最小的整数m。
具体方法是：先找到整数n对应的二进制数的最右边的1个1，从这个1开始，从右向左将连续出现的k个1变为0后，高1位的0变为1，再从最低位开始，将k-1个0变为1，即可得到最小的数n。
例如，32 对应的二进制数为00100000，将最右边的连续1个1变为0，高1位0变为1，即为01000000，对应整数为64。
又如，92 对应的二进制数为 01011100，将最右边的连续3个1变为0（得01000000），高1位变为1（得01100000），再将最低位的2（3-1）个0变为1，即为01100011，对应整数为99。
（4）源程序2。
#include <stdio.h>
int main()
{
int n,a,b,k,m;
while (scanf("%d",&n) && n!=0)
{
for (a=0; (n & (1<<a))==0; a++) ; // 找到最右边的1个1所在位置a
for (b=a; (n & (1<<b))!=0; b++) ; // 找到从a位开始向左的连续个1
m =n | (1<<b); // 把b位改成1
for (k=a; k<b; k++) m^=(1<<k); // 将从a位到b-1位的1全部取反变为0
for (k=0; k<b-a-1; k++) m |= 1<<k; // 将最低的b-a-1个位的0变为1
printf("%d\n",m);
}
return 0;
}
（5）编程思路3。
仔细琢磨整数的补码表示和位运算，可以将上面程序中的几个循环用一个表达式来完成。
1）按补码的表示法，正数的补码与原码相同，负数的补码是相应正数的补码的各位取反后加1。例如，以8位为例，32的补码是00100000，-32的补码是11100000；又如，92的补码是 01011100，-92的补码是 10100100。可以看出，把绝对值相等的正负两个整数用二进制数补码表示出来，从最低位开始到第1次出现1的地方为止，两者是一致的，高位部分的0和1恰好是相反的。利用这个特性，将正数m和相应的负数 –m进行逻辑与（&）的话，就能得到最初1出现的地方。
设x是整数n的二进制数保留最右边一个1，其余各位变为0后，所得到的数，则x = n&(-n)。
例如，n=92（01011100），则 -n=-92（10100100），x = n&(-n) = 01011100&10100100 = 00000100。
2）n＋x 是从右往左将整数n的第一个01转化为10。这是因为从最右边的一个1到第一个01，之间必然全是1，加上x后会一直进位，直到把01变为10，此时10的右边必然全是0。
例如，n=92，则 n+x=01011100 + 00000100=01100000。
3）表达式 n^(n+x) 可将整数n中最右边的第1个1开始，连续出现的1保留下来，且第1个01转化成的10中的1也保留下来，其余位全部为0。 n/x可以去掉最右边的所有0。
例如，n=92，n^(n+x) = 01011100^01100000 = 00111100。
n^(n+x)/x = 00111100/00000100 =00001111。
即 n^(n+x)/x 相当将k+1（k为从整数n的最右边的1个1开始，从右向左连续出现的1的个数）个1全部右移到最右边，且左边全部清0。由于最右边只需将k-1个0变为1，因此，将n^(n+x)/x /4可以右移两位，去掉两个1。
4）n+x+(n^(n+x))/x/4就是所求的最小整数。
（6）源程序3。
#include <stdio.h>
int main()
{
int n,x,m;
while (scanf("%d",&n) && n!=0)
{
x=n&-n;
m= n+x+(n^(n+x))/x/4;
printf("%d\n",m);
}
return 0;
}
26-2 二进制
本题选自洛谷题库 （https://www.luogu.org/problem/P2104）
题目描述
小Z最近学会了二进制数，他觉得太小的二进制数太没意思，于是他想对一个巨大二进制数做以下 4 种基础运算：
运算 1：将整个二进制数加 1
运算 2：将整个二进制数减 1
运算 3：将整个二进制数乘 2
运算 4：将整个二进制数整除 2
小Z很想知道运算后的结果，他只好向你求助。
（Ps：为了简化问题，数据保证+，-操作不会导致最高位的进位与退位）
输入格式
第一行两个正整数 n，m，表示原二进制数的长度以及运算数。
接下来一行 n 个字符，分别为‘0’或‘1’表示这个二进制数。
第三行 m 个字符，分别为‘+’，‘-’，‘*’，‘/’，对应运算 1，2，3，4。
输出格式
一行若干个字符，表示经过运算后的二进制数。
输入样例
4 10
1101
*/-*-*-/*/
输出样例
10110
（1）编程思路。
由于数据保证+，-操作不会导致最高位的进位与退位，因此直接根据运算符进行模拟运算即可。各算符的模拟运算方法分别为：
1）“+”: 从最后一个数（串中元素num[n-1]）开始向前搜索，直到遇到“0”为止，中途所遇到的每个字符“1”都变成字符“0”（相当于二进制数+1，且进位），最后遇到的“0”变成“1”。
2）“-”: 从最后一个数（串中元素num[n-1]）开始向前搜索，直到遇到“1”为止，中途所遇到的每个字符“0”都变成字符“1”（相当于二进制数-1，且向前借位），最后遇到的“1”变成“0”。
3）“*”：在字符串末尾增加一个“0”。
4）“/”：将字符串最后一位删除。
（2）源程序。
#include <stdio.h>
char num[100000000]={0},op[6000000];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
scanf("%s%s",num,op);
for (int k=0;k<m;k++)
{
int i;
switch(op[k])
{
case '+': for (i=n-1;num[i]!='0'; i--)
num[i]='0';
num[i]='1';
break;
case '-': for (i=n-1;num[i]!='1'; i--)
num[i]='1';
num[i]='0';
break;
case '*': num[n++]='0'; num[n]='\0';
break;
case '/': num[--n]='\0';
}
}
printf("%s\n",num);
return 0;
}
26-3 完全二叉搜索树
问题描述
二叉搜索树BST（Binary Search Tree）是这样一棵树，它或者是一棵空树，或者是一棵具有下列特性的非空二叉树：
（1）若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值。
（2）若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值。
（3）它的左、右子树也分别为二叉搜索树。
若一棵二叉树既是一棵满二叉树，又是一棵二叉搜索数，则这棵树是一棵完全二叉搜索树。例如，图1给出的就是一棵由1~15共15个整数构成的完全二叉搜索树。
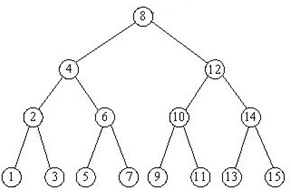
图1 一棵完全二叉搜索树
设有一棵由整数1~构成的完全二叉搜索树，编写一个程序，输入一个整数num（），输出在完全二叉搜索树中以该整数为根结点的子树的所有结点值中的最小值和最大值。例如，输入12，输出9和15；输入14，输出13和15；输入13，输出13和13。
输入格式
一个整数num。
输出格式
两个整数，分别表示以整数num为根结点的子树的所有结点值中的最小值和最大值。
输入样例
12
输出样例
9 15
（1）编程思路。
将个整数的完全二叉搜索树先构造出来，然后找到整数num所在的结点p，则以p结点为根的子树的中序遍历序列的第1个结点就是所求的最小值、中序遍历的最后一个结点就是所求得最大值。这样虽然能够解决问题，但显然不是一个好的办法。
将图1所示的完全二叉搜索树中整数全部写成二进制数，可以发现：
1）奇数全部在最底层。最底层数据的二进制数的最右边一定是1（即=1）。
2）倒数第2层为2的倍数，其二进制数据的最右边只有一个0，即=0、=1。
3）倒数第3层为4的倍数，其二进制数据的最右边有两个0，即=0、=0、=1。
4）倒数第4层为8的倍数，其二进制数据的最右边有三个0，即=0、=1。
将整数num（num=6、10、14、4、12、8）及所求的最小值和最大值列成如表1所示的表格。
表1 以num为根结点的BST的最小值和最大值（括号中为对应二进制数）
|
num |
最小值 |
最大值 |
|
6 （0110） |
5 （0101） |
7 （0111） |
|
10 （1010） |
9 （1001） |
11 （1011） |
|
14 （1110） |
13 （1111） |
15 （1111） |
|
4 （0100） |
1 （0001） |
7 （0111） |
|
12 （1100） |
9 （1001） |
15 （1111） |
|
8 （1000） |
1 （0001） |
15 （1111） |
观察表1中的二进制数据，不难得出结论：
1）以二进制数 X 为根的子树的最小值是将 X 最右之 1 换成 0，再加 1 所得的数。
2）以二进制数 X为根的子树的最大值是将 X 最右之1 右边的 0 全换成 1 所得的数。
设二进制数X最右边有连续k个0，若连续k个1组成的二进制数为P，则按上面的结论：最小值为X-P，最大值为X+P。
（2）源程序。
#include <stdio.h>
int main()
{
int a,p;
scanf("%d",&a);
for(p=2;a%p==0;p*=2);
p=p/2-1;
printf("%d %d\n",a-p,a+p);
return 0;
}
